-Rechnen

Die Mathematik baut (wie wohl kaum ein anderes Schulfach) rabiat aufeinander auf

(ja, das ist geradezu ihr Grundprinzip:

• alles

• mittels einiger weniger logischer Regeln

• aus möglichst wenigen offensichtlichen Grundannahmen [Axiomen] herzuleiten).

Nur ein Beispiel: beim Thema "Potenz(:-)rechnung" werden in dem Schulbuch schon auf den ersten Seiten zur Lösung der Aufgaben implizit verlangt:

• Assoziativ-, Distributiv- und Kommutativgesetz,

• die drei binomischen Lehrsätze,

• Bruchrechenregeln (vgl.   ),

• Wurzelrechenregeln,

... also alles "Dinge" aus teilweise viel früheren Schuljahren

(wobei natürlich zu ergänzen ist, dass diese "Dinge" auch zwischendurch immer wieder implizit vorkamen).

"Implizit" heißt dabei, dass es bei den Potenzrechenaufgaben

• vordergründig "nur" um das Lernen und Anwenden eben der Potenzrechenregeln geht,

• aber immer wieder o.g. "Dinge" eingemischt sind, ohne dass auf diese noch ausdrücklich hingewiesen wird

(also etwa "wende hier außer einer Potenzrechenregel auch den »ersten Binomi« an").

Weil die vollständige Lösung solch einer Aufgabe aber nur möglich ist, wenn

• eine (neu durchgenommene) Potenzrechenregel

• und der (uralte, längst vergessene oder aus dem Blick geratene) "erste Binomi"

angewandt werden, scheitern SchülerInnen oftmals nicht am neuen, sondern am alten Stoff.

Analog zum 5. Gebot aus dem Alten Testament, also

"Denn ich, der Herr, dein Gott, bin ein eifernder Gott, der die Missetat der Väter heimsucht bis ins dritte und vierte Glied an den Kindern",

könnte man also auch sagen:

"Wenn man einmal nicht aufgepasst oder etwas nicht verstanden hat, rächt sich das bis ins zwölfte oder dreizehnte Schuljahr."

Der "kasus knaxus" ist bei all dem wirklich das "implizit":

1. Wenn in der Rechnung eines Schülers alles schief geht

(oder er vor lauter Problemen überhaupt nicht rechnet),

merkt ein Lehrer oftmals gar nicht, dass es nicht am Neuen, sondern am Alten hapert.

2. Vor lauter Stoffdruck (Neues, Neues, Neues!) bleibt oftmals keine Zeit, das Alte explizit zu machen, also nochmals zu üben.

3. Und wie lange soll man denn das Alte wiederholen?: Bis auch der letzte es verstanden hat?

Wie bereits gesagt, müssen die SchülerInnen eine ganze Fülle von Gleichungen, nämlich

• Assoziativ-, Distributiv- und Kommutativgesetz,

• die drei binomischen Lehrsätze (im Folgenden kurz "Binomis" genannt),

• Bruchrechenregeln,

• Wurzelrechenregeln,

"können", d.h.

1. müssen (!) die SchülerInnen sämtliche Gleichungen jederzeit parat haben;

2. müssen die SchülerInnen die Gleichungen kennen

(z.B. den ersten Binomi, also ( a + b )² = a² + 2ab + b² );

dabei impliziert "kennen" natürlich:

3. müssen die SchülerInnen die Gleichungen in jedem Detail korrekt kennen

(z.B. darf beim ersten Binomi nicht das "gemischte Glied" 2ab vergessen werden, was in Analogie zum fatal ähnlich aussehenden Distributivgesetz, also (a + b) • 2 = a • 2 + b • 2, ein doch allzu naheliegender Fehler ist;  der scheinbar kleine Unterschied, ob

• eine 2 unten steht, also ein Koeffizient ist,

• oder ob die 2 [deutlich erkennbar!] oben steht, also ein Exponent ist,

ist also in Wirklichkeit ein gewaltiger Unterschied);

zudem dürfen die SchülerInnen nicht fatal ähnliche Gleichungen miteinander verwechseln

(z.B. ( a + b )² = a² + 2ab + b² mit ( a - b )² = a² - 2ab + b² ; man beachte insbesondere das korrekte + am Ende der zweiten Gleichung, obwohl in dieser zweiten Gleichung doch vorher nur Minus-Zeichen vorkamen!
Nebenbei: es wäre sogar wünschenswert, wenn die SchülerInnen sich die Gleichungen notfalls selbst herleiten und damit z.B. auch erklären könnten, warum in der zweiten Gleichung am Ende doch ein + vorkommt.

Nebenbei: der 2.-Binomi-Doppelfehler ( a - b )² = a² - b²  

[also einerseits ohne "gemischtes Glied" und andererseits mit hinten einem - ]

ergibt mit a² - b² genau das richtige Ergebnis des 3. [!]  Binomi, also von ( a  + b )(a  - b) = a ² -  b  ² )

4. müssen die SchülerInnen alle Gleichungen in beiden Richtungen beherrschen

(also z.B.

• ( a + b )² zu ( a + b )² = a² + 2ab + b²

• und umgekehrt a² + 2ab + b²  zu a² + 2ab + b² = ( a + b )²

vervollständigen können).

5. Und wehe, man benennt die Platzhalter nur mal um, also beispielsweise a in x und b in y

   (womit der 1. Binomi dann lautet: ( x + y )² = x² + 2xy + y² ).

   Oftmals kennen die SchülerInnen die Formeln zwar durchaus in ihren allgemeinen Formen, also mit den "Platzhaltern" a, b und ggf. c, aber sie haben

(trotz vielfacher Übung?)

nicht verstanden, was "Platzhalter" (oder "Variable") wirklich bedeutet, nämlich dass man da "alles und jedes" einsetzen kann.

Ein Beispiel: es sei a = 1 und b = t³.

Dann ergibt sich mit (diesmal) dem 3. Binomi

( a  + b )(a  - b) = a ² -  b  ²

( 1 + t³ )(1 - t³) = 1² - (t³)² = 1 - t⁶

In dieser Richtung (vgl. 4.) mag das noch einfach sein, aber es bedarf erheblicher Übung, um in  1 - t⁶

(in dem ja nicht mehr die Quadrate von a² -  b²  erkennbar sind)

1. t⁶ zu (t³)² zu "verkomplizieren" und dann

2. den 3. Binomi zu erkennen und - falls nötig - wieder in ( 1 + t³ )(1 - t³)  rück-zuverwandeln.

Man muss also einen "Blick" dafür gewinnen, dass

1. hinter 1 und t⁶ überhaupt jeweils was Quadratisches schlummert,

2. hinter "irgendwas² minus irgendwas²" vermutlich der 3. Binomi schlummert,

3. hinter "irgendwas²  plus   irgendwas²" hingegen vermutlich der Satz des Pythagoras.

Wegen all dieser Probleme wundert es mich

• kaum, dass viele SchülerInnen andauernd Fehler machen,

• viel mehr, dass einige fast fehlerlos "durchs Leben gehen".

Ich halte also Fehler für die Normalität - und meine fast (in aller Bescheidenheit :-), dass das die richtige Lehrereinstellung ist

(allerdings sollte ein Lehrer auch denjenigen "Futter" geben, die kaum mehr Fehler machen).

Ich höre aber auch schon den Einwand: "Wir haben's doch auch irgendwo, irgendwie, irgendwann gelernt."

Mir soll es im Folgenden um den fünften Punkt oben, also das Verständnis von "Platzhaltern" bzw. Variablen gehen.

Formeln wie etwa der erste Binomi, also ( a + b )² = a² + 2ab + b² , haben den immensen Vorteil, dass sie sehr knapp und damit

• überschaubar (= optische Ebene)

• und auch schnell sprechbar (= akustische Ebene)

("a plus b in Klammern zum Quadrat gleich a Quadrat plus zwei ab plus b Quadrat"),

• also doppelt gemoppelt (relativ) leicht merkbar sind.

Aber sie sind oftmals eben auch allzu suggestiv, denn da merkt "sich" doch allzu leicht die abstrakte Formel, aber nicht der Inhalt, wofür der Satz des Pythagoras bestes Beispiel ist:

a² +b² = c², also gesprochen in hübsch hüpfendem Versmaß "a Quadrat plus b Quadrat gleich c Quadrat"

können viele auch noch 20 Jahre nach dem Abitur runterrattern - ohne überhaupt noch zu wissen, wovon dieser Satz eigentlich handelt

(nämlich von geometrischen und rechnerischen Beziehungen in rechtwinkligen Dreiecken.

Nun ist das ja ein Nachteil aller allzu suggestiven Merkregeln:

• "drei - drei - drei, Issos Keilerei", aber was genau war im Jahre 333 [vor oder nach Christus?] in Issos [wo liegt das?], und wieso ist es überhaupt merkenswert?

• Oder ich kann noch so einige Merkregeln für die altgriechische Grammatik aufsagen, die einzelnen Wörter aber nicht mehr in griechischer Schrift schreiben und schon gar nicht sagen, was sie auf Deutsch bedeuten und welche grammatische Besonderheit sich hinter den runtergespulten Merksätzen verbirgt:

da verkommt Wissen zu Bildungsballast, mit dem man immerhin wunderbar angeben und auch gut seine konservative Einstellung raushängen lassen kann.)

Wohlgemerkt: es geht mir nicht darum, die Merkregeln abzuschaffen, wohl aber darum, sie zwischenzeitlich

(bis sie automatisch mit "Sinn" gefällt werden können)

aufzubrechen.

Und ein Mittel dazu ist eben das - bzw. "Schachtel-Rechnen":

Der 1. Binomi ( a + b )² = a² + 2ab + b² sieht dann beispielsweise folgendermaßen aus:

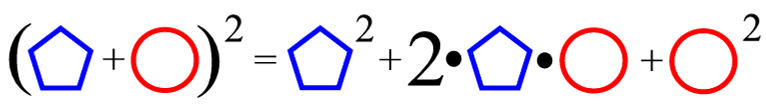
Bevor ich damit so richtig loslege, möchte ich aber doch unbedingt (wie immer) den Eindruck untergraben, dass ich hier ein Patentrezept entdeckt hätte

(während diese Patentrezepte in der pädagogischen Literatur ja gang und gäbe sind),

und zwar, indem ich (nicht nur hier) etwas tue, was LehrerInnen sonst viel zu selten tun

(vgl.   ),

nämlich untrennbare Vor- und Nachteile aufzähle:

1. sei sofort der doppelte immense Nachteil dieser Schachtel-Schreibweise genannt:

1. ist sie kaum mehr sprechbar, fehlt also die akustische Merkbarkeit,

2. sind die "Schachteln" bzw. Symbole (das Fünfeck und der Kreis) auf die Dauer sogar eher irritierend und ablenkend

(vgl.   ).

2. sind echte, dreidimensionale und beGREIFbare bzw. füllbare Schachteln allemal besser als  die (hier der Einfachheit halber benutzten) Symbole Fünfeck und Kreis.

3. scheint es mir allemal einer Überlegung wert, welche Form die Symbole (abgesehen von den unterschiedlichen Farben) haben sollen:

• sie sollten so unterschiedlich wie nur irgend möglich

• und gleichzeitig doch möglichst einfach sein, also keinerlei ablenkende Schnörkel enthalten

(es geht nicht um die Ästhetik, sondern ums Prinzip!).

Erst nachdem ich die Grafiken fertiggestellt habe

(und wo ich nun zu faul bin, alles nochmals zu ändern),

fällt mir aber auf, dass die beiden Kriterien besser erfüllt wären, wenn statt des (doch schon "irgendwie runden") Fünfecks ein simples Quadrat benutzt (und der Kreis beibehalten) worden wäre.

4. Das Schachtel-Verfahren

(und zwar mit der Eigenart, dass man in die Schachteln "alles und jedes" statt nur Mathematisches reinlegen kann)

ist zwar für viele der anfangs genannten Rechenregeln empfehlenswert

(z.B. für das Distributivgesetz:

es ist dasselbe,

• ob man 5 mal in den Laden geht und jeweils einen Hammer und eine Säge kauft, also

5 ● (H + S)

• oder ob man

  • beim ersten Einkauf 5 Hämmer

  • und beim zweiten Einkauf 5 Sägen

  kauft, also

  5 ● H + 5 ●  S:

das Distributivgesetz "codiert" ja gerade eine ganz alltägliche, "vormathematische" Erfahrung bzw. überstülpt sie nur mit einem komplizierten Namen).

Aber beispielsweise beim Satz des Pythagoras a² + b² = c² ist das Schachtel-Verfahren völlig unsinnig:

Apfel² + Birne² = Cocosnuss²  ???:

Wie soll aus einem Apfel und einer Birne zusammen eine Cososnuss werden? Und überhaupt: was - zum Teufel - soll ein Apfel (eine Birne, eine Cocosnuss) zum Quadrat sein? Ein quadratischer Apfel?!

Wir werden diesen logischen Schwurbeln unten beispielsweise auch beim 1. Binomi wiederbegegnen. Das entscheidende Problem beim Satz des Pythagoras ist aber, dass die außerhalb der reinen Formel a² + b² = c² liegende Hauptinformation, dass der Satz sich nämlich auf rechtwinklige Dreiecke bezieht, verloren geht, wenn man "alles und jedes" einsetzt.

5. Der entscheidende Vorteil von (am besten echten) Schachteln ist aber, dass sie

beGREIFbar und (mit allem und jedem!) füllbar sind und dass man sie (wie beim korrekten Umgang mit Klammern: ) wohl neben- und sogar ineinander stellen kann, sie sich aber nicht "überlappen" können (vgl. etwa  < [     >] ).

Damit aber zurück zu

Fangen wir also mit dem Füllen der (bislang noch leeren) "Schachteln" an, und zwar zuerst mal mit "allem und jedem", also noch nicht Mathematischem:

Besonders geeignet scheinen mir aber wegen des "gemischten Glieds" Doppelnamen bzw. zweisilbige Wörter, also z.B.

 

 

 

(sprich: "klim plus bim in Klammern zum Quadrat = klim Quadrat plus zwei plus bim Quadrat").

Das Klimbim-Beispiel wirkt aber vor allem lautlich, und analog könnte man den Sachverhalt auch mit Beethovens fünfter in die Schülergehirne rammen:

            

                                                      

                                                                                            

                                                                                                                                  

                                                                                                                                                                                                                                        

(Und da ich ja zwecks VeranSCHAUlichung oder -HÖRung weder Kosten noch Mühen scheue, kann man sich das Ergebnis sogar anhören, wenn man auf die Schaltflächen unter den Fünfecken bzw. Kreisen klickt.)

Oder hübsch wäre auch:

(Solche Sprüche sind nicht bloß Schnickschnack, sondern besonders gut geeignet, weil da überhaupt erst im "gemischten Glied" die beiden Bestandteile korrekt zusammentreffen: also in genau jenem "gemischten" Glied, das SchülerInnen

[in Analogie zum durchaus beherrschten Distributivgesetz, also (a + b) • 2 = a • 2 + b • 2]

so gerne vergessen.

Und sinnig ist etwa im letzten Bild auch, dass im "gemischten Glied" zwei Personen zusammentreffen.

Nebenbei: die beiden Polizisten sind auch jeweils die Dummheit ^{im Quadrat}!

[Ganz schön frech gegenüber der Obrigkeit, diese Astrid Lindgren!]

Höchst ungünstig wäre aber (H & M)², da dann falsch suggeriert würde: H² + 2 H & M + M².)

Oder - dann erst - allgemein

(und jetzt erst werden a und b nicht mehr als konkrete, unverwechselbare Buchstaben, sondern als beliebige Platzhalter deutlich)

,

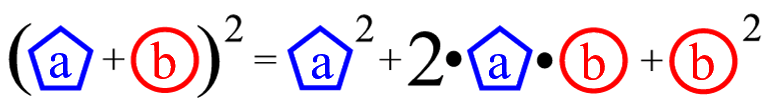wobei a und b "alles und jedes" sein können

(nur dass - wenn man erstmal mit dem Fällen einer Formel angefangen hat - für a bzw. b jeweils immer dieselbe Sache eingesetzt werden muss, also z.B.

• immer a = Hammer und b = Säge,

• aber nicht

  • einmal a = Hammer und das andere Mal a = Meißel

  • oder einmal b = Säge und das andere Mal b = Spachtel).

Unbedingt gleich mit zu erwähnen ist natürlich, dass die Wahl der Platzhalternamen beliebig ist, es also genauso gut

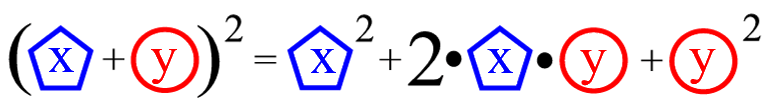
heißen könnte.

Jetzt erst setzen wir "Mathematisches" ein:

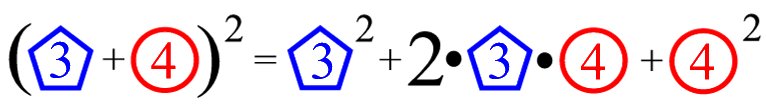
(... wobei der 1. Binomi allerdings für reine Zahlen eigentlich witzlos ist, da man ja sofort ( 3 + 4 )² = 7² = 49 rechnen würde)

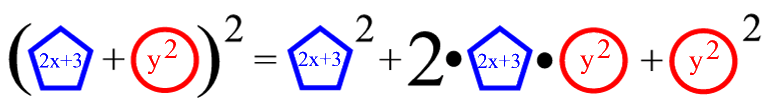
Und da dann wird endlich deutlich

(und das ist doch das Ziel all dieser Überlegungen),

dass man für a und b natürlich auch komplexere Terme einsetzen kann.

... und gleichzeitig deutet sich ein Problem an: wenn ich für echte Rechnungen endlich doch die Schachteln weglasse, muss ich stattdessen Klammern ergänzen, also einen Umweg gehen.

Aber immerhin deuten die Schachteln schon Klammern an!

Auch hier mischen sich natürlich (wie schon angekündigt) Denkschwurbel ein, denn was soll (?) beispielsweise "ein Hammer zum Quadrat" oder "Hammer mal Säge" bedeuten?!

Bzw. die Füllung der Schachteln mit Gegenständen bereitet - positiv gesehen - bereits die Abstraktion vor:

"Ist doch herzhaft egal, was »ein Hammer zum Quadrat« oder »Hammer mal Säge« bedeuten soll!"

PS:

Allemal klar ist, dass sich die Sätze natürlich nur mit mathematischen Schachtel-Inhalten herleiten und beweisen lassen.

Und so gesehen muss

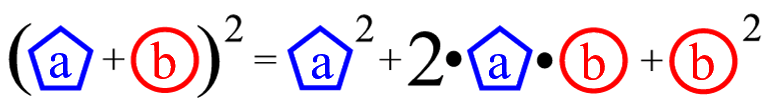
eben doch am Anfang stehen.