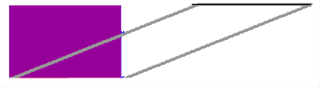
(Anfangs-/Endzustand)
Musterbeispiel Scherung / Spiegelung
Nichts Neues unter der Sonne?:
im üblichen Matheunterricht werden auf dem Standard"träger" Tafel/Papier von allen Bewegungen immer nur die Anfangs- und der Endzustände, aber nicht die sukzessive Übergänge gezeigt.
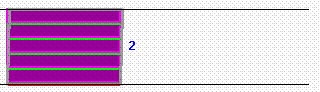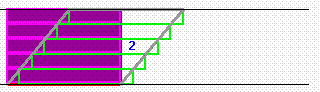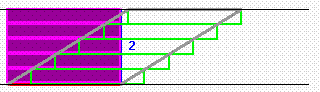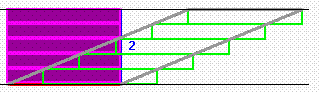
Ein Beispiel ist da die sogenannte "Scherung":
(Anfangs-/Endzustand)
Solches Vorgehen hat mehrere Nachteile:
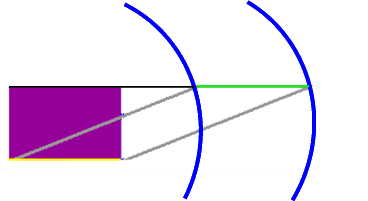
nicht intuitiv klar, dass die gelbe und die hellgrüne Strecke gleichlang sind;
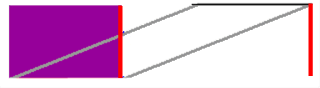
| Denn es ist doch im "Alltag" höchst ungewöhnlich, dass die Höhe (teilweise) außerhalb des Gegenstands (Parallelogramms) liegt - zumal solch ein Gegenstand sofort umkippen würde. |
erkennen SchülerInnen nicht, dass auch sämtliche Zwischenzustände zwischen Anfangs- und End-zustand (und darüber hinaus) dieselbe Flächengröße haben.
Nun wird die Scherung meines Wissens in der Schulmathematik ja überhaupt nur zweimal virulent, nämlich
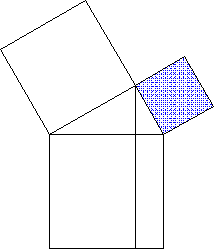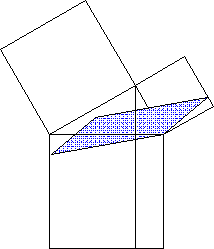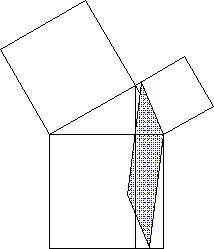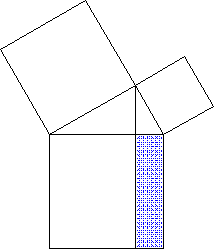
Diese seltene Benutzung der Scherung hat zur Folge, dass die SchülerInnen sie sowieso dann, wenn man sie Jahre später punktuell doch wieder braucht, (wie so vieles anderes) längst vergessen haben.
Wenn man sie dann aber wieder aufwärmt, zeigen sich eben prompt die oben genannten Probleme, insbesondere die mangelnde Vorstellungskraft für gleichbleibende Höhe.
Nun gibt's ja inzwischen "Dynamische Geometrieprogramme" - und eben auch ein Scherungsprogramm in meiner uralten Sammlung 
:
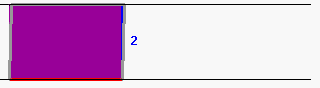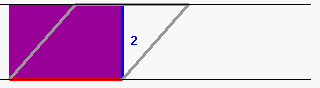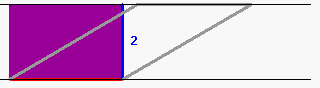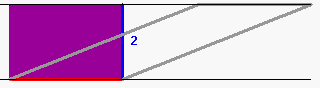
Besser noch (und darauf wird unten zurückzukommen sein) finde ich materielle, also anfassbar-begreifbare Modelle, also etwa
(vgl. 
)
Oder man denkt an Scheibenwischer
bzw. an die Ruder einer Galeere:
Und warum eigentlich heißt "das Ganze" überhaupt "Scherung":
Nun haben aber sowohl der Scheibenwischer und die Galeere als auch die "Doppel"-Scherung modellbedingte, leicht zu falscher Anschauung führende Nachteile:
die Höhe bleibt eben nicht immer gleich, sondern beispielsweise die Scheibenwischer werden manchmal (in ausgeschaltetem Zustand bei trockenem Wetter) ganz flach und verschwinden fast am unteren Windschutzscheibenrand.
Ein besseres Modell wäre da schon Folgendes (bei parallelen Schienen!):
(Man baue das mit Modellgleisen- und -zügen nach, wobei man Anfang und Ende der beiden Züge mit Gummibändern verbinde.)
.
Hier zeigen sich natürlich gleich wieder die Grenzen des (neuen) Modells: leider gibt es keine verformbaren Tassen (Topologie!), weshalb ich hier ein wenig mit einer Bildbearbeitung "mogle":
(Hübsch leicht "scherbar" sind Münzstapel
,
und zwar auch dann, wenn nicht alle Münzen gleich groß sind [s.u.]. Und mit diesen Münzstapeln wird auch schon das Cavalieri-Prinzip vorbereitet [s.u.].
Und ein netter Sonderfall ist nebenbei 
:
hat diese Tasse bei gleicher Grundfläche und Höhe [links!] nämlich dasselbe Volumen wie die anderen Tassen, denn dann kann die Tasse ja nur bis zum linken Rand gefällt werden, wenn sie nicht überlaufen soll,
ist ihr Volumen größer.)Im Dreidimensionalen wird die Scherung aber überhaupt erst um ihrer selbst willen
(und nicht nur als Hilfsmittel zur Dreiecksflächenberechnung und Herleitung des Kathetensatzes)
interessant:
zwar lässt sich auch noch im Zweidimensionalen zeigen, dass die Gegenstände nicht immer gleich breit sein müssen:
Aber besonders interessant wird's doch erst im Dreidimensionalen, wenn die Querschnitte in gleicher Höhe h zwar dieselbe Flächengröße A1 = A2, aber nicht mal dieselbe Flächenform (links Vollkreis, rechts Halbkreis mit größerem Radius) haben müssen:
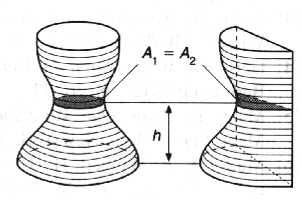
(wenn hier überhaupt noch von einer "Scherung" die Rede sein kann;
und zum Beweis sei auf das Cavalieri-Prinzip verwiesen, das zudem als Grenzwert- und insbesondere Integrationspropädeutik interessant ist:
)
Und jetzt noch kurz zur Spiegelung:
leider erfolgt eine (Achsen-)Spiegelung in einem (richtigen!) Spiegel mit Lichtgeschwindigkeit, also ohne jede (beobachtbare) Bewegung.
Vorstellungshilfen sind da "Die [Kinder-]Bücher mit den Folien" aus dem Meyers-Verlag:
