das mathematische

In dem Essay Bild hatte ich beklagt (schnief!), dass für SchülerInnen viele aus dem Alltag durchaus bekannte Wörter oftmals keinerlei Bedeutung mehr haben, sobald sie in der Mathematik auftauchen.

Viel schlimmer ist aber, dass sie mit vielen Dingen bzw. Vorgängen

(die von den Wörtern ja nur bezeichnet werden)

keinerlei alltägliche Bedeutung verbinden können, wenn diese Dinge bzw.  Vorgänge in der Mathematik auftauchen oder hilfreich wären:

  1. von wegen "auftauchen": dass in einer "Text-", also "Anwendungsaufgabe" direkter Bezug auf einen alltäglichen Vorgang genommen wird, beispielsweise also auf das "Überlappen" von Dachziegeln,
  2. von wegen "hilfreich wären": dass ein außermathematisches/r, der "Alltagswelt" zugehöriges/r Ding/Vorgang in einem mathematischen Zusammenhang gar nicht explizit genannt wird, aber zur Veranschaulichung sehr hilfreich wäre.
  1. Beispiel:

Aus der zweidimensionalen Vorlage 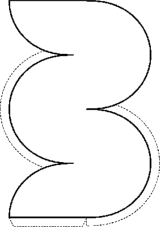soll "etwas" (Dreisimensionales) gebastelt werden. Was "etwas" dann für ein Körper ist, wird bewusst noch nicht verraten, sondern die SchülerInnen sollen sich erst langsam ins Dreidimensionale Denken "eindenken":

(am Ende sind allerdings auch die besonderen Eigenarten des Oloids durchzunehmen; diese Eigenarten sollen dann später in einer Ausstellung [s.u.] aber regelrecht er-fahren werden:

 ).

Beim gar nicht so einfachen Zusammenkleben von ergibt sich kurz vor Ende folgender Zwischenzustand:


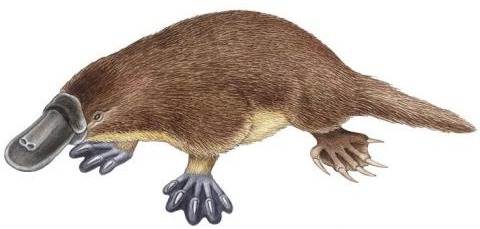
Und das sieht doch aus wie ein Schnabel, erinnert also z.B. an ein


Schnabeltier.

Dieses Schnabeltier-Beispiel ist vielleicht nicht besonders günstig, da die Erkenntnis "Schnabel(-tier)" arg spät kommt, nämlich dann, wenn wohl jeder schon die endgültige Oloid-Form erkennt. Das Schnabel-Bild ist also nicht gerade erkenntnisfördernd.

Immerhin hat sich das Wort "Schnabel" im Unterricht aber als günstig erwiesen, um über den Zwischenzustand reden und den letzten Tipp ("Schnabel zukleben [= halt' den Schnabel !]") geben zu können.

  1. Beispiel:

Ebenfalls für eine Mathematikausstellung sollen zwei (verschieden) große Modelle der Cheops-Pyramide gebaut werden.

Beim ersten Modell ist die Höhe (des Ausstellungsraums) gegeben, beim zweiten die Länge der Seitenkanten (= Dachlatten, s.u.)., was zu verschiedenen und auch unterschiedlich schweren Rechnungen führt, bei denen man sich teilweise "Hilfsstrecken" hinzudenken und in einem Fall zwei Mal nacheinander den Satz des Pythagoras anwenden muss:

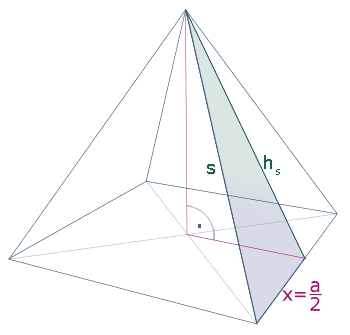
Sinn des Pyramidenbaus ist es u.a., die typischen Vorstellungsschwierigkeiten praktisch anzugehen. Insbesondere haben einige SchülerInnen enorme Probleme, in der zweidimensionalen Projektion die "richtigen" Strecken und die benötigten rechtwinkligen Dreiecke zu "sehen".

(Nebenbei: die Pyramidenmodelle werden auch gebaut, um die tatsächliche oder vermeintliche Mathematik der Cheopspyramide zu ergründen, also z.B. die Frage zu klären, ob es Zufall ist, dass die doppelte Seitenlänge durch die Höhe ziemich genau π [Pi]  ergibt, oder ob die Ägypter tatsächlich schon π  kannten - und warum sie sie dann so umständlich in der Pyramide versteckt haben.)

Zudem soll beim Bau immer überlegt werden,

(was diese Aufgabe ganz erheblich von sonst üblichen [vermeintlichen] Anwendungsaufgaben unterscheidet, die immer nur mathematisch gelöst werden sollen).

Ein Beispiel: SchülerInnen beherrschen vielleicht schon den Satz des Pythagoras, aber noch keine trigonometrischen Berechnungen, d.h. sie können wohl Seitenlängen, aber nicht Winkel berechnen und müssen daher benötigte Winkel durch das Zurechtlegen von Strecken herausfinden (ablesen).

Eines der beiden Pyramidenmodelle

(oder genauer: ein Kantenmodell )

soll aus 3 m langen Dachlatten montiert werden - und da erlaube ich mir einen kleinen Exkurs:

es ist doch wirklich zum Schreien komisch, was man im Internet alles zu hinterletzten Themen findet, nämlich hier z.B.

Damit aber zurück zu schnöden Dachlatten beim Pyramidenbau. Für das Kantenmodell sollen als erstes zwei einander gegenüberliegende Kanten

mit einem Winkeleisen verbunden werden. Solch ein im Baumarkt erhältliches Winkeleisen hat üblicherweise einen rechten Winkel, aber das ist ja nicht notwendig der Winkel an der Spitze der Cheopspyramide.

Hier sei nun vorausgesetzt, dass die SchülerInnen noch keine Winkel

(zwischen den beiden Latten an der Spitze 960)

 wohl aber Streckenlängen berechnen können. Wenn das Pyramidenmodell bei einer Kantenlänge von 3m maßstabsgerecht die Cheops-Pyramide wiedergeben soll, ergibt sich

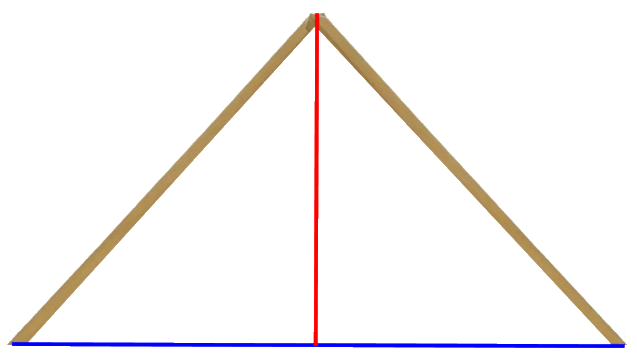
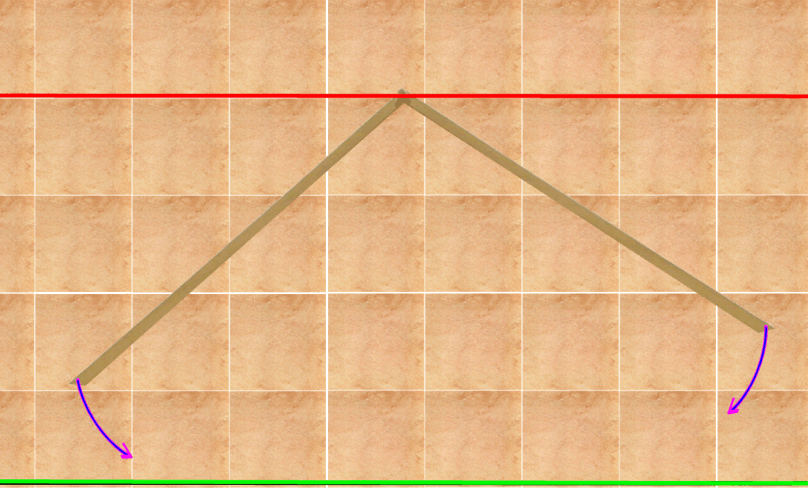
Womit sich nun die Frage stellt, wie man die beiden Kanthölzer nun konkret mit diesen Maßen zusammenmontiert.

(nebenbei: das geschieht in derselben Art, wie es auch in einer rein zeichnerischen Konstruktion funktionieren würde, nur dass die SchülerInnen jetzt

SchülerInnen neigen nun dazu, die beiden Hölzer genau so, wie sie hinterher in der Modellpyramide auftauchen, in die Luft zu halten und dann an der Spitze in zwei Meter Höhe miteinander zu verbinden, was natürlich eine ziemliche Wackelei setzt und zudem nicht ganz einfach (nur mit einer Leiter möglich) ist.

Viel einfacher sind folgende "Boden"-Verfahren, auf die die SchülerInnen aber mangels

leider kaum kommen:

man

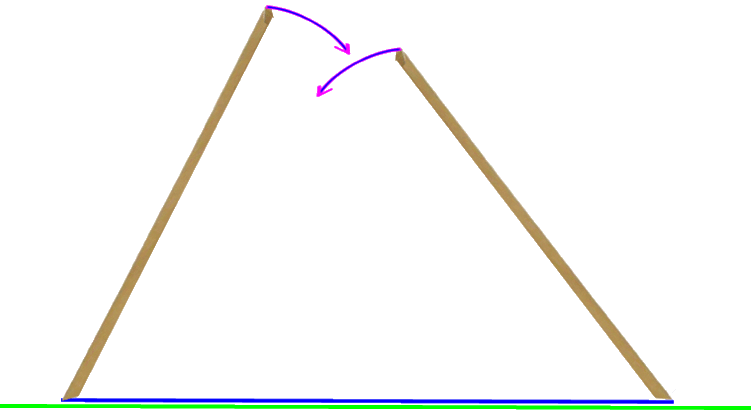
durch die schön ganzzahlige Höhe von 2 m kann man beispielsweise (falls im Klassenraum vorhanden) die Nähte eines Kunststoff-Fliesen-Bodens nutzen

(eben derart sollte man alle verfügbaren Gegebenheiten zu nutzen wissen - und überhaupt sehen),

um eine Parallele zur Raumwand in 2 m Entfernung zu erhalten. Dazu legt man die beiden Dachlattenspitzen zusammen auf diese Parallele und dreht danach die beiden losen Enden nur noch gegen die Wand: