Funktionen aufeinander schütten

Angenommen, die beiden Funktionen

• f:  y = x³ und
• g: y = x²

sollen addiert werden und wir wollen herausfinden, wie der Funktionsgraph der Summenfunktion h = f + g, also von h: y = x³ + x², aussieht.

Viele SchülerInnen stehen bei solch einer Aufgabe wie der Ochs vorm Berge, statt das Naheliegendste zu tun, nämlich eine Wertetabelle aufzustellen:

Kleine Zwischenbemerkungen:

1. haben die einfachsten und daher in der Schule durchgenommenen Funktionen ihr markantestes Verhalten

(Nullstellen, Schnittpunkt mit der x-Achse, Extrema, Wendepunkte)

fast immer für x-Werte in der Nähe des Ursprungs, so dass es naheliegt, in der Wertetabelle eben solche x-Werte zu wählen.

Und um einfache Rechnungen zu erhalten, ist es naheliegend, für x ganze Zahlen zu wählen, also z.B. -2, -1, 0, 1, 2.

2. Hilfreich sind im vorliegenden Fall noch zusätzliche Grundkenntnisse:

1. grundsätzliche Vorstellungen vom Aussehen der kubischen Funktion h: y = x³ + x²: dass sie also von links unten kommt und nach rechts oben geht;

2.  , dass sie für x = 0 eine doppelte Nullstelle hat und somit ihr Graph dort die x-Achse nicht schneidet, sondern nur berührt,

3. , dass sie somit zwischen -1 und 0 kurze "Zeit" oberhalb der x-Achse verläuft.

Damit ergibt sich als Graph der Funktion h: y = x³ + x²

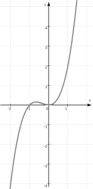
Noch viel einfacher wäre das zu erkennen, wenn man einen Funktionenplotter zur Hilfe nähme und ihn den Graph zeichnen lassen würde. Aber dann könnte man überhaupt nicht mehr erkennen, wie der Funktionsgraph zustande kommt.

Aber auch mit der Wertetabelle bleibt unklar, wie sich der Graph der Funktion h: y = x³ + x² aus den Graphen 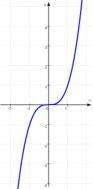der Funktion  f:  y = x³ und 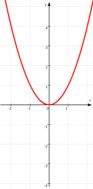der Funktion g: y = x² ergibt.

Manchmal scheint es mir ungünstig,

• von konkreten Funktionsgleichungen auszugehen,
• mit einer Wertetabelle die Funktionswerte zu ermitteln und
• damit dann den Funktionsgraphen zu zeichnen:

vor lauter Bäumen (Rechnen) sieht man dann oftmals den Wald (die "Funktionsweise" von Funktionsgraphen) nicht mehr.

Und deshalb "diskutiere" ich mit SchülerInneN

(auch schon in der Mittelstufe)

gerne Funktionsgraphen, deren Funktionsgleichungen wir gar nicht kennen oder für die gar keine Funktionsgleichungen zu finden sind

(z.B. Bergwanderungen, Gewinnverläufe ...).

Gegeben seien also

• nicht die zugrundeliegenden Funktionsgleichungen,
• sondern nur die                       Funktionsgraphen

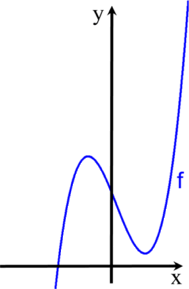und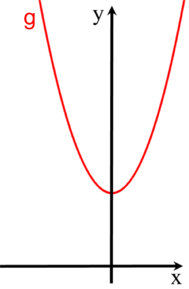

(wobei nicht verhehlt sei,
dass die Funktion f wie wie oben kubisch
und die Funktion g wie oben quadratisch zu sein scheint).

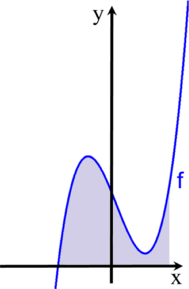
Nun stellen wir uns die beiden Funktionsgraphen als Berge aus hellblauem und rosa Sand vor

         ,

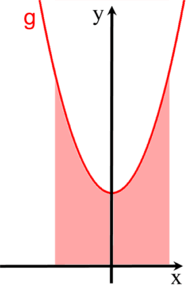legen sie beide übereinander

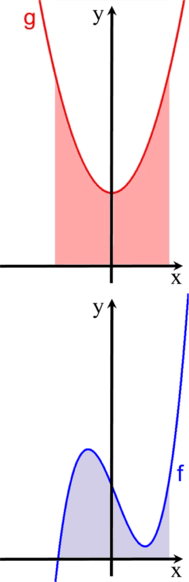
und lassen den rosa "Berg" auf den hellblauen "Berg" herabrieseln:

.

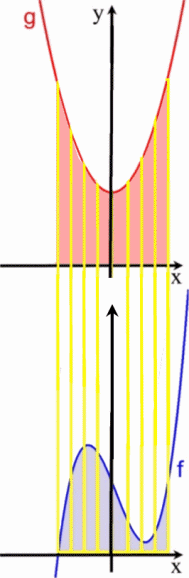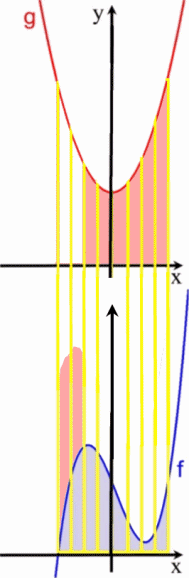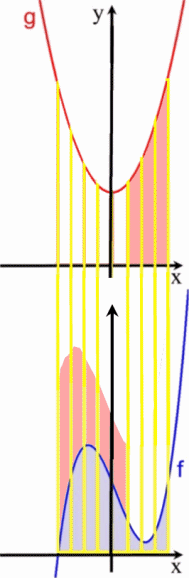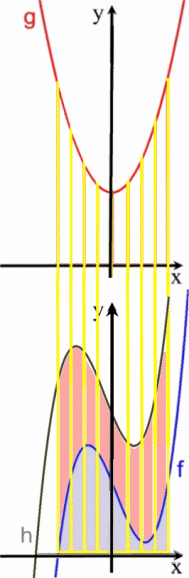
Als Gesamtberg h ergibt sich somit

.

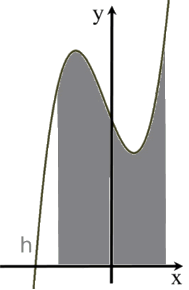Nun ist es in der Praxis nicht hilfreich, massenhaft Bergsegmente zu addieren, sondern es reicht, die Addition nur an wichtigen Stellen vorzunehmen. Solche wichtigen Stellen sind

• die Nullstellen der Einzelfunktionen (also für y = 0),
• die Schnittpunkte mit den y-Achsen (also für x = 0),
• ihre (Rand-)Extrema (Minima und Maxima):

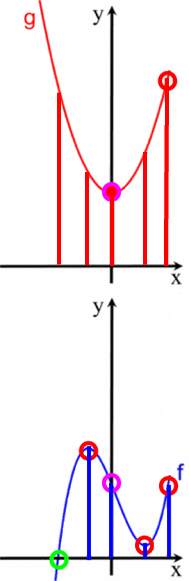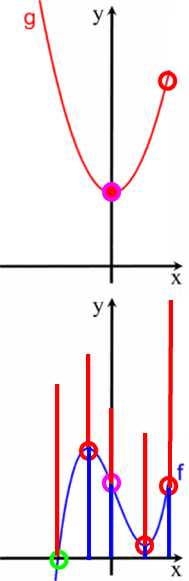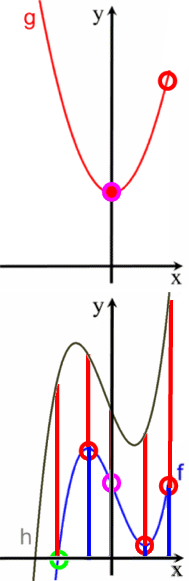
Und derart kann man Berge in Täler schütten und gilt der Bibelsatz:

"Alle Täler sollen erhöht werden und alle Berge und Hügel sollen erniedrigt werden, und was ungleich ist, soll eben, und was höckericht ist, soll schlicht werden":