sich frohgemut Schwieriges einhandeln
(um ein Problem zu vereinfachen)

Vgl. auch

Laien und insbesondere SchülerInnen mögen manchmal den Eindruck haben, in der Mathematik werde alles künstlich verkompliziert, also schwieriger gemacht, als es eigentlich notwendig wäre

(damit aber auch ja kein ach so dummer Laie es mehr versteht und man fein unter sich bleiben kann).

Mein Lieblingsbeispiel aus der Schulmathematik ist da die "Kongruenzlehre", in der ganz Simples

(dass ein Gegenstand sich nicht verändert, wenn man ihn dreht, schiebt oder spiegelt)

solange "theoretisiert" wird, bis die alltägliche Anschauung aber auch garantiert ausgetrieben ist.

Und es ist ja auch nicht zu bezweifeln, dass MathematikerInnen Spaß an komplexen Aufgaben um ihrer selbst willen haben, also das lieben, was viele SchülerInnen am liebsten vermeiden

(bzw. erst mühselig lernen müssen),

nämlich sich an komplexen Aufgaben "abzuarbeiten" - und mit einem Beweis sich selbst zu beweisen.

Ansonsten gelten in der Mathematik aber vier kleine "Glaubenssätze":

1. "Alles sollte so einfach wie möglich gemacht werden, aber nicht einfacher."
   (Albert Einstein)
2. Als schön wird empfunden, was (möglichst) einfach ist, und wenn etwas schön ist, vertrauen die MathematikerInnen

(bei aller mathematik-typischen radikalen Skepsis gegenüber Vermutungen),

darauf, dass es auch richtig ist

(vgl. ). 

3. Wenn man etwas Schwieriges/Neues (z.B. krumme Graphen, Kreise und Kugeln) nicht kann, nähere man es

(und zwar erstaunlich gut und überhaupt nur auf diesem Weg möglich)

mit Einfachem/Bekanntem (Rechtecken, Dreiecken) an

(vgl. ).

4. , und darum geht es mir hier vor allem:

Zu 4.:

Wie man sich Kompliziertes einhandelt, um damit dann doch zu einfachen Lösungen zu kommen, sei anhand der drei Hauptvertreter der Irrationalität, nämlich den Zahlen

• ≈  1,414213562373,
•  π ≈  3,141592653589,
•  e  ≈  2,718281828459,

gezeigt

(womit gleich unterstellt wird, irrationale Zahlen seien ganz schrecklich kompliziert).

Wenn man im einfachsten überhaupt denkbaren geometrischen Gegenstand, nämlich einem Quadrat mit der Seitenlänge 1, die einfachste überhaupt denkbare Linie, nämlich die Diagonale d, zeichnet, steht man gleich vor einem Riesenproblem:

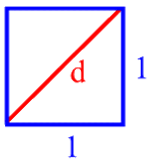
Es lässt sich nämlich zeigen, dass die Länge dieser Diagonale d eben nicht mehr einfach, sondern und damit irrational ist

(vgl. )

Hier sei nicht weiter darauf eingegangen, dass dieses Ergebnis für SchülerInnen oftmals "gehirnausrenkend" ist, da die mit ihren unendlich vielen (und zudem chaotisch aufeinander folgenden) Nachkommastellen ja immer länger und länger zu werden scheint, während die Quadratdiagonale doch offensichtlich fest ist.

Sondern mich interessiert hier nur, dass wir uns bereits bei einem ganz simplen Beispiel die höchstkomplizierte Zahl eingehandelt haben. Bislang ist alles nur (unerwartet schnell) schwierig geworden, und da stellt sich doch die ungeduldige Frage, wann das Versprechen der zweiten Satzhälfte von

"manchmal muss man Kompliziertes in Kauf nehmen, um ein Problem dann doch einfach zu lösen"

eingelöst wird:

1. können wir mit der immerhin und überhaupt erst die Länge der Diagonale d bestimmen, wobei allerdings ein (angeblich) höchst unangenehmer Wert herauskommt.
2. können wir überhaupt erst mit Wurzeln endlich alle quadratischen Gleichungen lösen (soweit sie denn lösbar sind).
3. ist die sowieso nur dann schwierig, wenn man (immer mit dem Taschenrechner in der Hand) fatal auf ihre Dezimaldarstellung starrt wie das Kaninchen auf die Schlange.

In "Wirklichkeit" aber ist die eine (was allerdings gewöhnungsbedürftig ist) ganz normale Zahl wie jede andere auch, und dementsprechend kann man auch ganz normal mit ihr rechnen

(z.B. ist 2             + 3            = 5     

              2 Elefanten + 3 Elefanten = 5 Elefanten).

Erschütternd einfach ist die aber vor allem deshalb, weil ()² exakt gleich 2 ist. Mehr (also etwa die Dezimaldarstellung von ) muss man auch wahrhaft nicht wissen.

4. eröffnet die aber, wie oben schon angedeutet, ganz neue, hochinteressante Perspektiven, nämlich auf das Reich der irrationalen Zahlen

(was - vielleicht arg unbefriedigend - hier nicht genauer erklärt sei).

2. π

Der Kreis als "krummes Ding" ist, wie bereits oben angedeutet, etwas geradezu typisch Mathematisches, weil

• selbst die schlausten MathematikerInnen grundsätzlich nicht (direkt) mit Krummem umgehen können

(vgl. ),

• sie sich mit Geradem (Rechtecke, Dreiecke) aber dennoch wunderbar an den Kreis annähern können.

Einziger Nachteil ist, dass sie sich dabei die scheußliche (?) Zahl π ≈ 3,141592653589, also wieder eine irrationale Zahl, einhandeln.

(Man könnte fast meinen, dass der Kreis regelrecht hinterhältig ist: er kommt so einfach daher und offenbart dann doch [erstmals] die totale Unvereinbarkeit von Krummem und Geradem.)

Fragt sich nur wieder, was wir denn mit der Einführung der komplizierten (?) Zahl π gewonnen haben:

1. ist sie auch nur wieder eine ganz normale Zahl, mit der sich prächtig rechnen lässt, und zwar selbst dann, wenn man nicht mal ihren (immer nur ungeführen) Dezimalwert kennt.
2. reicht doch für jede Anwendung π = 3,14 (oder gar einfach nur 3), und das ist doch wahrhaft keine sonderlich komplizierte Zahl.

(Nebenbei: wenn einem das Rechnen mit bzw.  π zu kompliziert ist, rechne man doch erstmal mit den Näherungen 2 bzw. 3, und wenn man fertig ist, ersetzt man wieder jede 2 durch bzw. jede 3 durch π . Nur Vorsicht: zwischendurch nie etwas [z.B. 2 + 1] ausrechnen. Vgl. ) 

3. brauchen wir nur die eine (einzige) Zahl π, um sämtliche Aufgaben zu Kreisen, Kugeln, Kegeln und Zylindern lösen zu können, denn in allen Gleichungen für deren Umfang / Oberfläche / Volumen taucht (erstaunlicherweise!) immer nur dieselbe Zahl π auf

(vgl. ).

Bei soviel Anwendbarkeit sollte es nicht mehr schwer fallen, dafür frohgemut die Zahl π in Kauf zu nehmen. 

4. eröffnet auch die Zahl π neue, hochinteressante Perspektiven, nämlich u.a. auf das Reich der transzendenten Zahlen

(was hier ebenfalls nicht genauer erklärt sei).

3. e

Obwohl die Zahl e ≈   2,718281828459 so scheußlich schief und krumm ist, taucht sie doch an allen Ecken und Enden der Mathematik auf

(und zwar, was um so frappierender ist, scheinbar völlig unabhängig voneinander).

Hier sei nur ein Anlass gezeigt, bei dem sie auftaucht, und auch dieser Anlass soll nicht mathematisch fundiert ausgearbeitet werden:

es ist tatsächlich möglich, unter allen Exponentialfunktionen der Form y = a^x (also z.B. y = 2^x oder y = 3^x) eine (einzige!) zu finden, deren Ableitung f ' mit der Ausgangsfunktion f identisch ist.

Das allein ist doch schon erfreulich genug, denn so kann sogar jeder Idiot diese Funktion unendlich oft ab- und wieder aufleiten (integrieren).

Der kleine Nachteil besteht aber darin, dass die einzige Funktion, bei der das klappt, eben y = e^x ist, man sich also leider unvermeidlich die scheußliche (?) Zahl e ≈ 2,718281828459 einhandelt.

Ohne weitere Erklärung sei noch erwähnt, dass man dann auch alle anderen Exponentialfunktionen (also z.B. y = 2^x oder y = 3^x) ableiten kann, indem man sie sämtlich auf die Funktion y = e^x zuRückführt

(allerdings mit den zusätzlichen kleinen Schönheitsfehlern, dass man sich dann auch noch unvermeidbar den natürlichen Logarithmus sowie die Kettenregel einhandelt).

So genau muss man , π und e ja auch gar nicht kennen, sondern eigentlich nur wissen, dass es "irgendwelche" Zahlen sind, mit denen gerechnet wird wie mit jeder anderen (einfacheren) Zahl auch.

Also z.B.:

•           3       +        3         = 2 •       3           ,
• + = 2     ,
•               +              = 2 •               .

Bei jeglichen Anwendungen reichen sowieso Näherungswerte, also z.B. = 1,4 .

Ansonsten aber ist es geradezu kontraproduktiv, die Dezimalwerte aufzuschreiben bzw. sich vom Taschenrechner anzeigen zu lassen:

1. , weil , π und e allesamt irrational sind, wir also höchstens Näherungswerte aufschreiben können, die zudem
2. viel scheußlicher (höchst unregelmäßig, da eben irrational) aussehen als die Kürzel , π und e.
3. heben sich die "schiefen" Werte sowieso oftmals im Laufe von Rechnungen auf

(vgl.   ),

nämlich z.B. bei • = 2 : genau genommen ist • = ()² = 2 ja sowieso das Einzige, was ich über weiß.

Ein anderes Beispiel ist die in 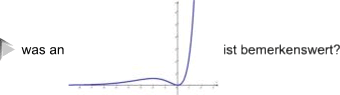angedeutete Bestimmung der Extremwerte der Funktion f: y = e^x • x² .

für diese Rechnung muss man "nur" zweierlei wissen und stumpf anwenden:

1. , dass die Ableitung von g: y = e^x wieder e^x ist, dass also g ' (x) = e^x,

(überhaupt nur deswegen hatten wir uns ja e eingehandelt!),

2. die Produktregel, also: f(x) = g(x) • h(x) f '  (x) = g' (x) • h (x) + g (x) • h ' (x).

Mit beidem zusammen folgt:

f '  (x) = g' (x) • h (x) + g (x) • h ' (x)

f '  (x) =   e^x   •   x²   +   e^x  •   2x  .

Um nun

(was eine Standardaufgabe ist)

die Extremwerte der Funktion f zu finden, setzt man das Ergebnis gleich Null und erhält

               e^x   •   x²   +   e^x  •   2x  = 0
          e^x     • (x²   +             2x) = 0

Nun kann aber

(und das ist nebenbei einer der wichtigsten mathematischen Tricks; vgl. )

das Produkt aus e^x und (x²   + 2x) nur dann gleich Null sein, wenn

1. entweder der erste   Faktor, also        e^x     , gleich Null ist,
2. oder der         zweite Faktor, also (x²   + 2x), gleich Null ist.

Zu a.: man muss von der Funktion g: y = e^x gar nichts wissen, außer dass sie nie Null wird.  Somit bleibt nur die Möglichkeit b., dass also (x²   + 2x) = 0 ist. Und da ergibt sich sehr einfach, dass das entweder für x = 0 oder für x = -2 der Fall ist:

Man schleppt also die Funktion g: y = e^x die ganze Zeit mit, ohne viel von ihr zu wissen, und am Ende fällt sie (glücklicherweise!) völlig raus.

Zweifelsohne hat das aber den Nachteil, dass schnell vor lauter stumpfer Algorithmenanwendung jegliche Vorstellung abhanden kommt. Das aber ist fast notwendige Folge einer Schulmathematik, in der die e-Funktion kaum um ihrer selbst willen interessiert, sondern nur als Beispiel für die Ableitung und Integration einer zusätzlichen Funktionenklasse

(zusätzlich zu den ganz- und gebrochen rationalen Funktionen).

Oben war ich weitgehend die Antwort schuldig geblieben, welche mathematischen Perspektiven sich denn durch , π und e ergeben.

Die erstaunlichste Perspektive zeigt sich dabei

(wenn man statt der die betrachtet und  [allerdings nicht ganz sauber] i = definiert)

in einer der schönsten aller mathematischen Gleichungen, nämlich Eulers Gleichung

e ⁱ + 1 = 0

(vgl. ).

Es lässt sich nur schwer erklären, warum diese Gleichung aufgeht, aber doch leicht zeigen, weshalb sie in Mathematikeraugen so schön ist:

weil sich in ihr drei (scheinbar völlig voneinander unabhängige) scheußliche Zahlen,  nämlich i = sowie e und π, gegenseitig aufheben und zusammen exakt das simple Ergebnis - 1 ergeben.

Es ist, als hätten i = sowie e und π voneinander gewusst und sich dazu verabredet, die Gleichung e ^{i π} + 1 = 0 zu erfüllen.

Man könnte die Gleichung e ^{i π} + 1 = 0 auch als unverhoffte "Hochzeit der Mathematik" bezeichnen (ein flotter Dreier), weil da verschiedenste, scheinbar völlig voneinander unabhängige mathematische Gebiete zusammenfinden.