das sagt sich so einfach:

vgl.


"Über sieben Brücken musst du geh'n,
sieben dunkle Jahre übersteh'n,
siebenmal wirst du die Asche sein,
aber einmal auch der helle Schein."

Einem Deutschen werden die siebeneckigen britischen Münzen beim ersten Mal sicherlich auffallen.

Aber vermutlich scheinen sie ihm dann doch nicht weiter bemerkenswert und schon bald selbstverständlich.

Merkwürdig finde ich es schon, dass viele Leute

(hier siebeneckige Münzen)

hinaus gehen, d.h.

(wie werden solche Münzen entworfen und hergestellt?)

(warum gibt es solch ungewöhnliche Münzen?)

fragen.

(Solche Leute sind wie die derzeit gängigen "science"-Museen: ich habe es jüngst noch im in London erlebt, wo teilweise phantastische Exponate gezeigt werden, aber kaum eine Möglichkeit geboten wird, die Exponate [auch historisch] zu verstehen

[wobei der Verstehensprozess ja keineswegs rein verbal allein über erklärende, also oftmals gängelnde Texte vermittelt werden muss]:

in solchen "science"-Museen

Warum aber bleiben auch die allermeisten "science"-Museen bei den Effekten stehen?:

      1. , weil auch die Museums-Leute nicht über die Effekte hinaus denken können?
        2.
      1. , weil auch bei ihnen inzwischen ausschließlich die "Quote" zählt, also die Besucherzahlen?
        2.
      1. , weil sie vor der [vermeintlichen?] Idiotie der Museumsbesucher resigniert haben, diese also im Grunde verachten?
        2.
      1. gar, weil die Museums-Leute die Besucher für dümmer halten, als diese tatsächlich sind, und damit
        2.
[wie im Privatfernsehen]

das dumme Angebot die dumme Nachfrage überhaupt erst erzeugt?)

Natürlich kann man nicht andauernd nach den Hintergründen ("wie" und "warum") der Phänomene/Effekte fragen: wer das täte, würde sich endlos in den Hintergrund-Verzweigungen verlaufen

und nie wieder zu einer

finden.

Nochmals: was mich wundert, ist, dass viele Leute

Nun vermute ich aber mal, dass diese Leute

(vor allem durch Schulen und Medien)

abgewöhnt

Man muss in einer nunmal arbeitsteiligen Gesellschaft eigentlich nur noch wenig oder (fast) gar nichts mehr (ganz) können, aber es tut doch gut, überhaupt irgendwas

(Menschliches oder Technisches)

zustande zu bekommen bzw. schonmal zustande bekommen zu haben.

Im Folgenden beschäftige ich mich aber nur mit dem Zustandebringen von Technischem.

Wenn jemand

(" , und überhaupt waren die Menschen im Mittelalter alle dumm")

und daher auch nicht dankbar ist,

hilft manchmal die Aufforderung

.

Dabei reicht es, dass der Aufgeforderte nur mal kurz erzählt, wie er etwas

(z.B. sowas Simples wie )

selbst herstellen würde: schon in den scheinbar einfachsten Fällen würde wohl schnell klar, dass sie in Wirklichkeit heillos schwierig sind, nämlich doch schon

voraussetzen - mal ganz abgesehen vom genialen "Funken", der oftmals hinter einer technischen Neuerung steckt:


(Thomas Alva Edison in seinem Labor)

Angenommen mal, wir wollen eine siebeneckige Münze herstellen. Dieses Vorhaben gliedert sich in zwei Schritte:

  1. den Entwurf einer Vorlage:
    1. die Konstruktion eines (gleichseitigen) Siebenecks ,
    1. die künstlerische Gestaltung der Reliefs auf beiden Seiten .
  1. die materielle Herstellung mindestens einer Münze nach dem Entwurf aus A.

Mich interessiert daran nur der mathematische Teil A.a., d.h. die Konstruktion eines (gleichseitigen) Siebenecks.

Heutzutage ist ja alles bereits fertig: wenn ich ein Siebeneck brauche

(aber wer braucht das schon?),

Hier haben wir schon wieder ein enormes pädagogisches Problem: wenn alles schon fertig ist, wieso soll man es

(sozusagen das siebeneckige Rad )

nochmals neu erfinden?

(Nebenbei: es gibt erstaunlich viele Autos mit 7-Speichen-Felgen. Warum?)

Immer eine gute Frage ist es, wie ein absoluter (mathematischer) Laie an eine Aufgabe herangehen würde. In unserem vorliegenden Fall z.B. so:

3600 : 7 = 51,428571 0 = 51,428571428571428571428571...0

So genau, wie die periodischen Nachkommastellen es vorgeben, kann man sowieso nicht zeichnen, weshalb wir der Einfachheit halber sagen:

3600 : 7 ≈ 510

Damit ergibt sich als Konstruktion eines Siebenecks:

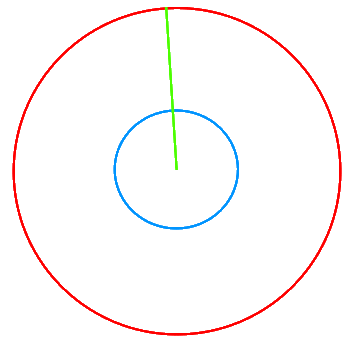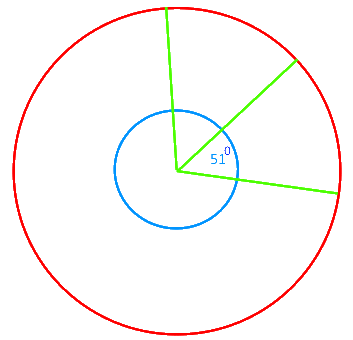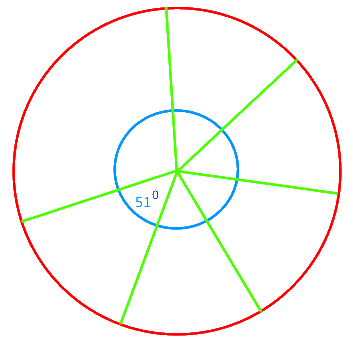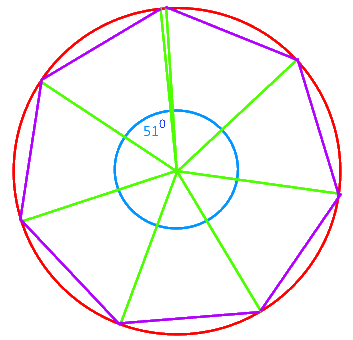
Dabei interessiert es unseren Laien nicht die Bohne und ist es bei einer relativ kleinen Münze auch unerheblich, dass 510 nur ein Näherungswert ist:

7 • 510 = 3570,

d.h. am Ende sind es lächerliche 30 zu wenig:

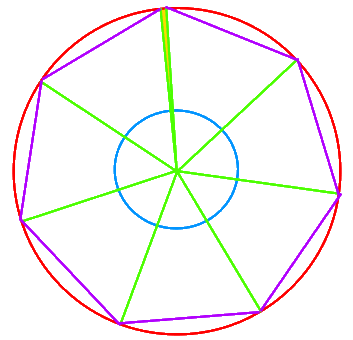
Nur am Rande sei erwähnt, dass die Siebenecksseiten der britischen Münzen keine (geraden) Strecken, sondern rundlich sind. Da die sieben Rundungen aber Kreisausschnitte mit demselben Radius sind, lassen sie sich leicht konstruieren, wenn man erstmal das Siebeneck hat:

(Nebenbei: mir ist nie vorher aufgefallen, dass auch die europäische -Münze ein verkapptes Siebeneck ist.

"Als Spanische Blume (spanisch flor española) wird die an eine Blüte erinnernde Form einer Münze bezeichnet. Sie weist sieben gleichmäßig am Rand verteilte Einkerbungen auf und geht auf eine spanische 50-Peseten-Münze [ ] zurück, die ab 1991 geprägt wurde. Diese besondere Prägung wurde eingeführt, um blinden und sehbehinderten Menschen die Unterscheidung der Münze von anderen Werten zu erleichtern. Wegen der sieben Einkerbungen (Siebeneck) gilt die Münze numismatisch als „nicht rund“."
[Quelle: ];)

Nun aber folgt ein geradezu paradoxer Sprung, der viel über die Denkweise von Mathematikern, ja, das "Wesen" der Mathematik aussagt - und vielen Laien fremd ist

(eine interessante, hier aber nicht beantwortete Frage wäre es da, ob und wie man Schülern diesen Sprung ermöglichen und "schmackhaft" machen kann):

  1. : einerseits kann man sowieso nicht absolut genau zeichnen

(z.B. nicht 51,428571 0-Winkel),

  1. : anderseits fragen sich Mathematiker aber dennoch, ob und - wenn ja - wie man ein exaktes Siebeneck zeichnen könntete

(der falsche Konjunktiv "könntete" ist kein Druckfehler, sondern Absicht, um den Irrealis zu betonen, der den Mathematikern herzhaft egal ist).

Der offensichtliche Widerspruch zwischen a. und b. ist für Mathematiker folgendermaßen auflösbar:

(laut Platon "Ideen"),

die allein im Kopf funktionieren.

Ein Beispiel:


Präzisionszirkel

einen Kreis zu zeichnen versucht, wird man dennoch nie einen exakten Kreis

(also streng genommen überhaupt keinen Kreis)

erhalten, weil selbst ein bestens angespitzter Bleistifteinsatz eine unter dem Mikroskop "krümelige" Spur hinterläßt:

(... was allerdings einen Laien wohl kaum stört, da die Ungenauigkeit mit bloßem Auge gar nicht zu erkennen ist und wohl nur Korinthenkacker, die immer was zu mäkeln finden, einen Kreis unters Mikroskop legen;

 nebenbei: Mathematiker legen einen realen Kreis natürlich nicht tatsächlich unter ein Mikroskop

 [woher nehmen und nicht stehlen?],

 sondern sie wissen auch so, dass dieser Kreis da "zackelig", also nicht-perfekt ist).

Mathematik ist also vor allem "Denkgymnastik": nach einem zugegebenermaßen ziemlich (logisch)rigiden Fitnessplan

(der allerdings glücklicherweise auch noch genügend kreative Freiheiten läßt!) 

schlank werden im Kopf und

Wichtig für den Versuch einer Siebenecks-Konstruktion ist es auch, welche Zeichenmittel man überhaupt zuläßt: klassischerweise sind das seit den Alten Griechen nur Zirkel und Lineal, also das "perfekt Runde" und das "perfekt Gerade".

Wie nun aber "der Fürst der Mathematik"


Carl Friedrich Gauß
(1777-1855)

bewiesen hat:

"[...] dass nur die [gleichseitigen] p-Ecke (p ist eine Primzahl) konstruierbar sind, bei denen es natürliche Zahlen k gibt, so dass p = + 1 Primzahlen sind.
Das sind die n-Ecke mit der Eckenzahl 3, 5, 17, 257 und 65537. Weitere Zahlen sind nicht bekannt [...]"
(Quelle: )

Diese Aussage enthält erhebliches Fachchinesisch, läßt sich aber dennoch halbwegs verstehen:

  1. handelt die Aussage nur von gleichseitigen Vielecken, deren Eckenzahl eine Primzahl ist, also von gleichseitigen Dreiecken, Fünfecken, Sieben(!)ecken, Elfecken usw.;

weil also z.B. gleichseitige Vier- und Sechsecke keine Prim-Eckenzahlen haben, sind sie von der Aussage nicht betroffen, und in der Tat lassen sich gleichseitige Vier- und Sechsecke exakt (und relativ einfach) konstruieren:


Beispiel Sechseckskonstruktion
(Quelle: )

  1. : der Ausdruck p = + 1 sei an sechs Beispielen erklärt:
p = + 1 =
   = + 1 =
   =   2      + 1 =
           =           3            

oder kurz

        p =          3         ;

weil 3 eine Primzahl ist, ist laut der obigen Gauß-Aussage das gleichseitige 3-Eck exakt mit Zirkel und Lineal konstruierbar

(was ja in Schulen auch bis zum Erbrechen durchgeführt wird);

p =   + 1 =
   =   + 1 =
   =   4       + 1 =
   =            5          

oder kurz

        p =             5         ;

weil 5 eine Primzahl ist, ist laut der obigen Gauß-Aussage auch das gleichseitige 5-Eck exakt mit Zirkel und Lineal konstruierbar:

(Quelle: ;
weil aber [wie wir gleich sehen werden] eine exakte Konstruktion des Siebenecks nicht möglich ist,
würde ich Schüler im Unterricht  "immerhin" die
[wenn auch nicht einfache] Fünfeckskonstruktion durchführen lassen);

p = + 1 =
   = + 1 =
   =  16     + 1 =
   =          17          

oder kurz

       p =          17        ;

weil 17 eine Primzahl ist, ist laut der obigen Gauß-Aussage auch das gleichseitige 17-Eck exakt mit Zirkel und Lineal konstruierbar:

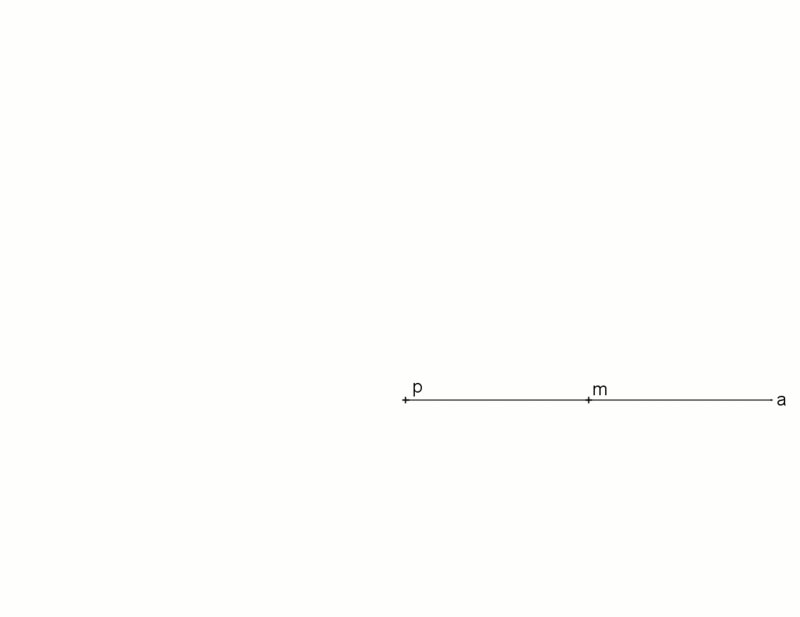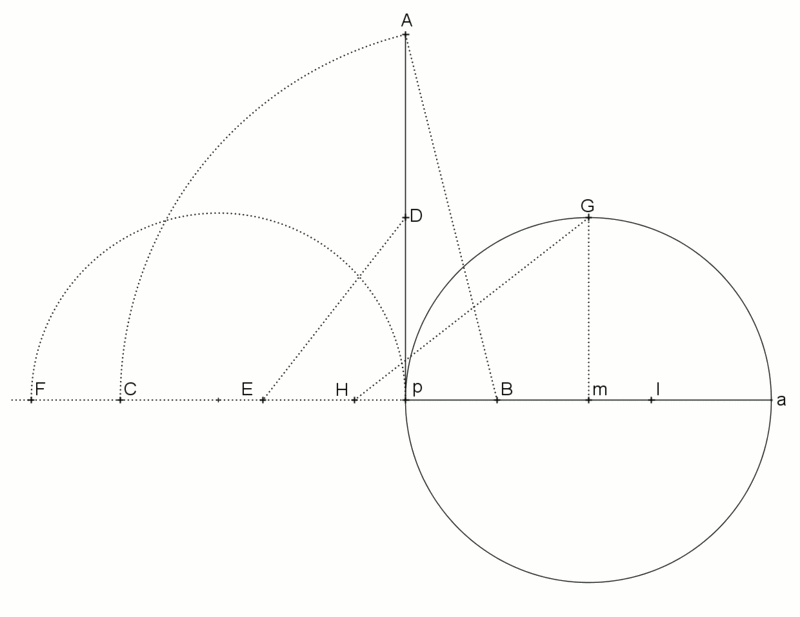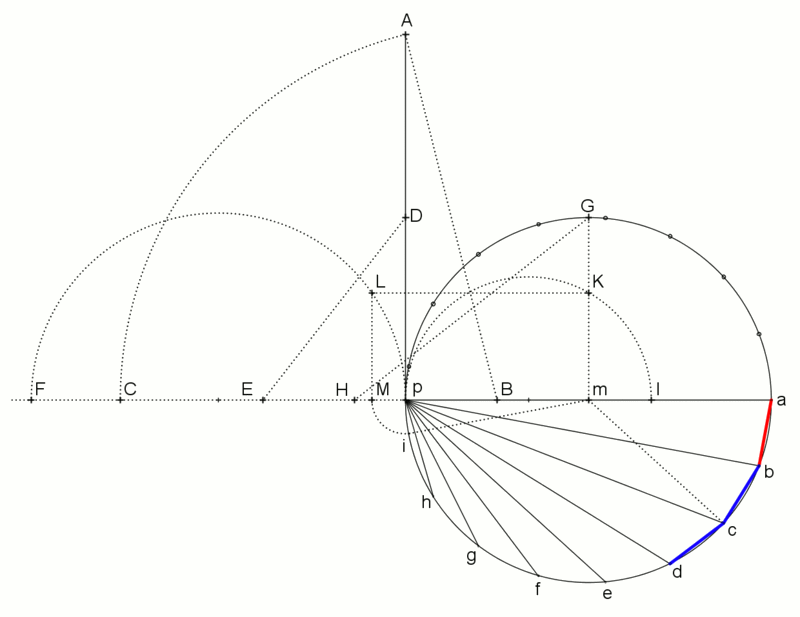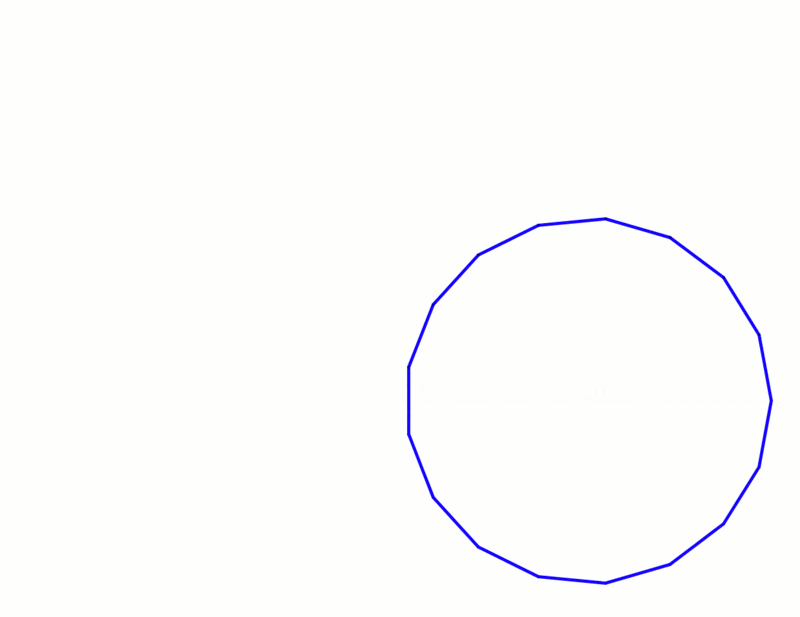
(Quelle: ;
dabei sei mal dahingestellt, dass die 17-Eck-Konstruktionen ohne Erklärungen kaum verständlich ist; hier soll das Wissen reichen, dass die exakten Konstruktionen tatsächlich möglich ist);

p =    +   1 =
   =    +    1 =
   =  256     +    1 =
   =           257         

oder kurz

p =           257           ;

weil 257 eine Primzahl ist, ist laut der obigen Gauß-Aussage auch das gleichseitige 257-Eck exakt mit Zirkel und Lineal konstruierbar;

p =        +      1 =
   =         +      1 =
   = 65536      +      1 =
   =              65537       

oder kurz

p =              65537     ;

weil 65537 eine Primzahl ist, ist laut der obigen Gauß-Aussage auch das gleichseitige 65537-Eck exakt mit Zirkel und Lineal konstruierbar;

p =                          +           1 =
   =                          +           1 =
   = 4294967296             +           1 =
   =                         4294967297      

oder kurz

p =                         4294967297         ;

Nun ist aber 4294967297 keine Primzahl, denn 4294967297 = 641 • 6700417. Weil aber 4294967297 keine Primzahl ist, ist das gleichseitige 4294967297-Eck laut obiger Gauß-Aussage nicht exakt konstruierbar.

(So ganz nebenbei kann man hier enorm Wichtiges lernen: ob 65537 [für k = 4] oder 4294967297 [für k = 5] Primzahlen sind, kann man "mit bloßem Auge" gar nicht erkennen, sondern dafür bedient man sich z.B. eines Online-Primfaktor-Zerlegungs-Programms wie etwa .

Für k = 6, k = 7, k = 8 usw. kommen aber durch die die doppelte Potenz in der Formel p = + 1 schnell gigantisch große Zahlen heraus, bei denen selbst Supercomputer

[die also auch nicht viel schlauer als Menschen sind]

nicht herausfinden können, ob sie Primzahlen sind und ob somit das entsprechende p-Eck konstruiert werden könnte.

Genau deshalb ist bis heute unbekannt, ob es gleichseitige n-Ecke mit n > 65537 gibt, die laut dem Satz von Gauß exakt konstruiert werden könnten.

Und weil sogar Großcomputer nicht herausfinden können,

werden heutzutage in Computern fast sämtliche Informationen mit Primzahlen verschlüsselt:   )

Vielleicht versteht man das noch bis hierhin - aber wohl kaum den Beweis der Gauß-Aussage:

ich unterstelle mal, dass dieser Beweis derart schwierig ist, dass auch ich ihn kaum oder erst nach langwieriger Einarbeitung verstehen würde

(und deshalb habe ich erst gar nicht im Internet nach diesem Beweis gesucht).

Wenn aber schon ich als halbgebildeter Mathelehrer diesen Beweis wohl kaum verstehen würde, haben Laien und Schüler sicherlich nicht die mindeste Chance, da überhaupt irgendwas zu verstehen.

Aber man muss ja eben nicht

(wie sonst in der Schule üblich)

alles verstehen

(und gerade deshalb nach dem Prinzip "ganz oder gar nichts" oftmals gar nichts):

selbst wenn man einen mathematischen Zusammenhang nur halb oder auch nur ansatzweise versteht, kann man doch "nebenher" unendlich viel "anderes" verstehen

(vgl. ):

z.B. lernt man beim Problem, ob ein Siebeneck exakt konstruierbar ist, Grundlegendes über mathematische Denkweisen, ja, die Quintessenz dessen, was Mathematik eigentlich ist.

Eine der aberwitzigsten Errungenschaften der Mathematik ist dabei Folgendes:

(man müsste schon ziemlich durchgeknallt sein, um sich an die Konstruktion eines 65537-Ecks [auf einem riesigen Blatt Papier?] zu setzen).

Aber zurück zum gleichseitigen Siebeneck. Da ist festzuhalten:

gibt es kein ganzzahliges k, für das unsere 7 rauskommt, ist also das Siebeneck nicht exakt konstruierbar

(und z.B. das 11- oder 13-Eck auch nicht).

Die Münze kann daher schon allein aus ganz grundsätzlichen (mathematischen) Gründen

(also mal ganz abgesehen von den Problemen der handwerklichen Anfertigung)

nur ein ungefähres, nicht absolut exaktes gleichseitiges Siebeneck sein.

Immerhin gibt es aber Näherungsverfahren für die Konstruktion des gleichseitigen Siebenecks

(vgl. hier: ).

Diese Näherungsverfahren könnte man zwecks "Fingerübungen" mit Zirkel und Lineal nachkonstruieren, aber das bliebe doch arg unbefriedigend, da man nicht versteht, weshalb welche Konstruktion durchgeführt wird.

Viel interessanter ist die merkwürdige Beschränkung auf die Hilfsmittel Zirkel und Lineal, die seit der Antike eingehalten wird und doch sehr willkürlich erscheint.

Denn es gibt durchaus Verfahren, mit denen man ein exaktes (!) Siebeneck konstruieren kann, aber eben Verfahren, in denen (zusätzlich) andere Hilfsmittel eingesetzt werden

(vgl. hier: ).

Besonders interessant finde ich aber die Konstruktion exakter (!) Siebenecke mittels Origami:

  1. , weil Schüler Spaß an (endlich mal!) solch manueller Arbeit haben könnten,
  2. , weil mit Origami einige Konstruktionen möglich sind, für die immer das Dogma bestand, dass sie (allerdings nur mit Zirkel und Lineal) unmöglich seien;

nun sehe ich ja gerne Dogmen stürzen , aber als ich erfuhr, dass beispielsweise die berühmte Winkeldreiteilung mittels Origami doch möglich ist

(vgl. ),

hatte ich das Gefühl, jahrzehntelang durch das "Geht-nicht"-Dogma reingelegt worden zu sein.

Hier also exakte Konstruktionen des Siebenecks mittels Origami:

Bislang blieb aber offen, warum die britische Münzanstalt mit so ungewöhnlich geformte Münzen herausgebracht hat.

(Bzw. vielleicht ist der Grund derselbe wie oben bei der "Spanischen Blumen": damit Blinde und Sehbehinderte die Münzen besser von ähnlich großen runden Münzen unterscheiden können.)

Eine direkte Antwort auf die warum-Frage habe ich aber im Internet nicht finden können, weshalb ich hier in "grundsätzlichere" Gefilde ausweiche:

die Zahl 7 ist in vielen Kulturen und insbesondere in unserer westlichen Kultur mit vielen Bedeutungen aufgeladen bzw. ein Symbol für verschiedenste "Dinge". 

(Wohlgemerkt "Symbol": eine Zahl bedeutet außer der durch sie mit einem Namen versehenen Anzahl rein gar nichts; z.B. steht die Zahl 3 für die Anzahl von drei Dingen, also für die Anzahl von 3 Autos, 3 Babys, 3 Gedanken usw. Sie steht aber nicht für die Autos, Babys oder Gedanken selbst.

Weil die Zahl 3 aber nur die Anzahl bedeutet, ist sie von den 3 Autos, 3 Babys und 3 Gedanken ablösbar und bedeutet dann "nur" noch "3 Dingsbums"

[egal, welche Dingsbums es sind].

Normalerweise haben Autos, Babys und Gedanken nichts miteinander zu tun.

[Ich könnte allerdings eine Geschichte konstruieren, die sie zusammenbringt:

"Mein erster   von 3 Gedanken war, das erste   von 3 Babys in das erste   von 3 Autos zu setzen.
 Mein zweiter von 3 Gedanken war, das zweite von 3 Babys in das zweite von 3 Autos zu setzen.
 Mein dritter   von 3 Gedanken war, das dritte   von 3 Babys in das dritte    von 3 Autos zu setzen."]

Wenn die 3 aber von den Dingen abgelöst ist, also nur noch eine Anzahl bedeutet, kann ich verschiedene 3 Dinge fast paradoxerweise doch wieder in einen Zusammenhang bringen: die 3 Autos, 3 Babys und 3 Gedanken haben immerhin ihre Anzahl gemeinsam.

Wozu dieser lange Einschub?: weil ich im Gegensatz zu vielen Zahlengläubigen ["Numerophilen"] natürlich nicht glaube, dass der 3, der 7 (!) oder z.B. der oder

irgendeine andere Bedeutung "zueigen" [sozusagen eingebaut] ist als eben die Anzahl.)

Mein Unglaube an eine andere inhärente Bedeutung der 7 außer der Anzahl hält mich

(als [ehemaligen] Mathe- und Deutschlehrer, also auch Geistes"wissenschafter")

natürlich nicht davon ab, mit großem Interesse und noch größerer Freude dabei zuzuschauen, wie die 7 im Laufe der Geschichte dennoch mit verschiedensten Bedeutungen aufgeladen worden ist, und zwar so sehr wie sonst wohl nur die 3.

Der wichtigste Grund dafür, dass ausgerechnet die 7 derart überfrachtet wurde, scheint zu sein:

"Die Sieben ist die Summe von drei und vier, von Geist und Seele einerseits sowie Körper andererseits, also das Menschliche. In der überkommenen christlichen Zahlensymbolik des Mittelalters steht die Drei für die nach dem Bild des dreifaltigen Gottes geschaffene Seele und alle geistigen Dinge. Die Vier ist die Zahl der Elemente und steht damit symbolisch für die materiellen Dinge, die nach antiker Anschauung alle aus der Kombination der vier Elemente hervorgehen."
(Quelle: )

Die 7 steht als Summe aus 3 und 4 also für den gesamten Kosmos

(Himmel und Erde ).

Der Wikipedia-Artikel nennt massenhaft weitere Bedeutungen der 7, die ich hier nicht ausführlich zitieren möchte, aber allemal einer genaueren Recherche

(auch im Mathematikunterricht!)

würdig sind!

Hier nur einige Beispiele dafür, wie omnipräsent die 7 auch in der heutigen Populärkultur ist:

      ...