SpannendES

 spannendER 

machen

(Cantors Unendlichkeiten)

 

 

"[Cantors] Beweis gehört zu den Weltwundern - in eine Reihe mit den hängenden Gärten der Semiramis oder den Pyramiden von Gizeh."
(Palle Yourgrau)

"Aus dem Paradies, das Cantor uns geschaffen, soll uns niemand vertreiben können."
(David Hilbert)

"Vor einiger Zeit verbrachte ich einen Nachmittag in einer Schule im Norden von Paris, einem der »benachteiligten« Vorstadtviertel. Immer wieder erinnerten mich die Schüler daran, daß sie bloß Vorstädter seien und einer aus der Vorstadt nun mal nicht so intelligent sein könne wie einer aus Paris. All die Theorien über die geistige Unterlegenheit bestimmter Gruppen oder gar bestimmter »Rassen« nahmen sie für bare Münze; verbannt in ihr Vorstadtviertel und größtenteils aus weit entfernten Ländern stammend, waren sie sich sicher, für die Naturwissenschaften nicht geschaffen zu sein und »Mathe nie zu kapieren«.
Würde diese Annahme irgendeiner Wirklichkeit entsprechen, wäre ich traurig darüber, müßte diese naturgegebene Ungleichheit jedoch akzeptieren. Aber obgleich sich in den geistigen Leistungen fünfzehnjähriger Jugendlicher durchaus Unterschiede zeigen, hat das, abgesehen von pathologischen Fällen, mit der Natur nichts zu tun. Diesen Vorstadtjugendlichen bewies ich das am eigenen Leib. Gemeinsam beschäftigten wir uns mit Mathematik, besser gesagt, wir spielten mit Mathe, und sie begeisterten sich für Cantors verschiedene »Unendlichen«. Wir machten einen Umweg über den Satz von Gödel, und die Aufmerksamkeit ließ nicht nach. Ich denke, sie haben mir geglaubt, als ich ihnen am Ende sagte, daß sie fähig seien, ebensoviel zu verstehen wie jeder durchschnittliche Abgänger einer renommierten Technischen Hochschule."

zitiert nach Bild

Vielleicht scheidet nichts so sehr die Geister wie das mathematische Teilgebiet "Zahlentheorie":

Ein ganz simples Beispiel:

Gegeben seien Zahlen, die aus drei Mal derselben Kombination von zwei Ziffern gebildet sind, also z.B.

oder allgemein

Durch welche Zahlen sind alle diese Zahlen teilbar?

(Nebenbei, die gesuchten gemeinsamen Teiler sind, wie sich beweisen lässt, trivialerweise 1 sowie 3, 10101 und 7)

Auch für mich ist diese Frage völlig uninteressant - und völlig konstruiert. Aber es gibt eben Leute, die

Oder zwei andere, unten noch wichtig werdende Beispiele:

  1. Wenn (ja wenn!?) ich mit einer ultraspitzen Nadel auf den Zahlenstrahl piekse

(wobei die utopische Nadelspitze genauso breit sein müsste wie eine Zahl, also unendlich schmal):

wie groß ist dann die Wahrscheinlichkeit, dass ich dabei eine rationale, algebraische oder aber transzendente Zahl treffe?
 (was mit diesen Begriffen gemeint ist, wird erst unten erklärt)

  1. Ein Mann geht in einem zwei Meter langen Raum nacheinander immer die Hälfte der (bis zur Tür) noch übrigbleibenden Strecke, also

Der Mann hat offensichtlich "Schwellenangst" vor der Tür (hinter der beispielsweise seine Schwiegermutter lauert): er geht und geht und geht (wenn auch immer kleinere Schritte) - und kommt doch nie an.

Gerade als MathematiklehrerIn kann man sich gar nicht deutlich genug klar machen, wie sehr sich hier die Geister scheiden:

zu 1.: a) Wieso sollte ich mit irgendeiner Nadel dämliche Zahlen aufpieksen?
                  ("Haben die MathematikerInnen denn eigentlich nichts Besseres zu tun?")

         b) Solch ultrafeine Nadeln, wie in der Voraussetzung gefordert, gibt es ja
             (aus ernsthaft physikalischen Gründen!) gar nicht.

zu 2.: a) Was soll solch eine blödsinnige Gehweise?

         b) So beliebig kleine Schritte, wie sie hier auf die Dauer vorkommen, kann ein
             Mann ja gar nicht machen - mal ganz abgesehen davon, dass kein Mensch
             jemals immer kleinere (jeweils halb so große) Schritte macht.

(Und siegt hier nicht der "gesunde Menschenverstand"?: in der Tat sind unendlich kleine Schritte physiologisch gar nicht möglich, ja nicht mal physikalisch: irgendwann - um das sowieso schon schwachsinnige Beispiel dennoch mal bis an seine Grenzen zu denken - ist die "Schrittgröße" auf Elementarteilchengröße, und kleiner "geht's" - zumindest bisheriger Kenntnis nach - nicht.

Schon hier wird deutlich, mit welch weltfremder Abstraktion MathematikerInnen ganz selbstverständlich umgehen - die Laien völlig fremd ist.

Und doch behaupte ich schon hier: eine Geschichte [und sei's mit klischeehafter Schwiegermutter] kann eben doch ansonsten abgeneigte Laien ködern, wobei natürlich dieses "Ködern" etwas Hinterhältig-Irreführendes an sich hat.)

Der normale Laien-, also oftmals auch Schülerverstand verweigert sich also schon der Problemstellung (Voraussetzung "wenn")  - und kann und will daher gar nicht mehr zur eigentlichen Mathematik (Folgerung) kommen.

(Genau das ist nebenbei auch das tödliche Problem bei vielen  angeblich ach so "lebensweltlichen Anwendungsaufgaben".)

In 1. ist sogar schon das "ich" falsch: "ich", das ist vielleicht der Mathematiker

(der allzu leichtfertig unterstellt, auch andere könnten und wollten sich in die gegebene Situation reindenken),

aber bestimmt nicht der desinteressierte Laie.

Und eins ist allemal klar:

(entweder die ZahlentheoretikerInnen oder aber die Laien haben von Anfang an einen genetischen Schaden).

Ich habe hier den Begriff "Zahlentheorie" sehr weit gefasst:

Zahlentheorie, Zweig der Mathematik, der sich mit den Eigenschaften und Beziehungen von Zahlen beschäftigt. Gemäß dieser breiten Definition gehört vieles der Mathematik zur Zahlentheorie. Im Allgemeinen beschränkt sie sich jedoch auf die Untersuchung der natürlichen und der ganzen Zahlen [...]"
(Bearbeitet von: Eckart Maus; zitiert nach: Microsoft Encarta)

Ein Musterbeispiel ist da wieder Fermats letzter Satz, der ja besagt, dass es für natürliche n ≥ 3 KEINE natürlichen Zahlen a, b und c gibt, so dass

an + bn = cn

Ich zähle hier aber auch Cantors Überlegungen zu kontinuierlichen (statt nur diskreten) Zahlenmenge und in Folge davon seine UnendlichkeitsÜberlegungen mit zur Zahlentheorie.

Anlass für meine Überlegungen hier ist das Buch

Bild

  1. ist dieses Buch schon vom Untertitel her so ganz nach meinem Geschmack, nämlich endlich mal Bild im besten Sinne.

(Und so ganz nebenher möchte ich ja behaupten, dass man

  • dieses Buch im Schulunterricht [zusätzlich zu den üblichen Schulbüchern oder noch besser statt ihrer] durchnehmen kann - und sollte,

  • durchschnittlichen SchülerInnen [und sowieso den mathematisch leistungsstärkeren] durchaus Cantors Unendlichkeitsüberlegungen "zumuten" kann bzw. sie ihnen gar nicht vorenthalten darf - wobei allerdings manchmal auch Mut zur Lücke angesagt ist, wenn die benötigte Mathematik partiell allzu schwierig wird.)

Die Stärke von Aczels Buch besteht ja gerade darin, dass er nicht wild drauflos assoziiert

("nunja, die Kabbalisten haben sich auch um die Unendlichkeit gekümmert, aber Cantor hat den hebräischen Buchstaben »Aleph« nur benutzt, weil die lateinischen und griechischen Buchstaben schon anderweitig in der Mathematik vergeben waren"),

sondern überzeugend zeigt, wie Cantors mathematische Überlegungen zur Unendlichkeit aus einer jüdischen Tradition erwuchsen - und dass sie mit einer ganz persönlichen Tragödie verbunden waren.

  1. liegt mir hier eine Grundsatzkritik an dem Buch fern. Ganz im Gegenteil! Wie so oft bei guten Büchern bin ich ja überhaupt erst durch dieses Buch auf meine an es anschließenden Gedanken (und auch Verbesserungsvorschläge) gekommen

(und es wäre ja sogar schon fast Leichenschöndung, als Ausgangspunkt ein wirklich schlechtes Buch zu nehmen).

  1. hätten meine Hinzufügungen unten natürlich zur Folge, dass Aczels Buch noch dicker würde

(wenn ich auch nur an einer, nämlich eben gerade der unten behandelten Stelle genauer und - wie ich hoffe - verständlicher argumentieren würde).

Die Entscheidung zwischen "so dünn wie möglich" und "so dick wie nötig" ist sicherlich nicht leicht zu fällen. Zudem könnte man natürlich sagen, dass Aczel sein übergreifend kulturelles Thema nicht hinter allzu viel Mathematik verbergen durfte, weil sich Laien dann vielleicht doch schnell ausgeklinkt hätten

("ach, doch alles wieder nur Mathematik - und alles andere [Kulturelle] wie gehabt nur als vorgeschobener Anlass").

Mir scheint aber, dass Aczel zumindest bei der Abzählbarkeit der algebraischen Zahlen (s.u.) mathematisch genauer hätte sein müssen, wenn er nicht einen Bruch seiner Argumentation an zentraler Stelle wagen wollte.

Dennoch, so einiges hätten Wir - mit Verlaub - doch  besser gemacht!

Um das zu "beweisen", sammle ich hier erst mal drei Stellen aus dem Buch, die ich dann "nachbessern" möchte. Dabei geht es mir zentral um die zweite Passage, zu deren Verständnis man aber auch die erste und dritte braucht

(wobei ich zu Kürzungen gezwungen bin: ich hoffe, dass sie sinngemäß sind und der gekürzte Text weitgehend verständlich bleibt):

  1. "Offenbar stießen die Griechen auf die Idee des Unendlichen, weil sie sich lange Zeit erfolglos mit den Paradoxen herumschlugen, die dem Philosophen Zenon von Elea (495-435 v. Chr.) zugeschrieben werden. In dem bekanntesten dieser Paradoxen beschreibt Zenon einen Wettlauf zwischen Achill, dem schnellsten Läufer der Antike, und einer Schildkröte. Da die Schildkröte viel langsamer ist, bekommt sie einen Vorsprung. Nun argumentierte Zenon folgendermaßen: Wenn Achill den Punkt erreicht, von dem die Schildkröte das Wettrennen begonnen hat, ist die Schildkröte ein Stück vorangekommen. Zu dem Zeitpunkt, da Achill diese Strecke zurückgelegt hat, ist die Schildkröte wiederum ein Stück vorangekommen. Und so geht es fort ad infinitum. Also könne der schnelle Achill, so Zenons Schluss, die langsame Schildkröte niemals überholen. Aus diesem Paradox leitete Zenon die Behauptung ab, unter der Voraussetzung, dass Raum und Zeit unendlich teilbar seien, könne es keine Bewegung geben.
    Ein anderes Paradox von Zenon, die Dichotomie, besagt, dass Sie das Zimmer, in dem Sie sich gerade befinden, nie verlassen können. Zunächst legen Sie die halbe Entfernung bis zur Tür zurück, dann die Hälfte der restlichen Strecke, dann die Hälfte der Distanz, die Sie nun noch von der Tür trennt, und so fort.

[vgl. das einleitende Beispiel oben]

Selbst mit unendlich vielen Schritten - jeder halb so groß wie die vorangehenden

[manchmal enthält das Buch an entscheidenden Stellen fatale Übersetzungsfehler; hier - wo es noch eher unwichtig ist - müsste es richtig heißen: "wie der vorangehende"]

- können Sie nie durch die Tür kommen! Hinter diesem Paradox steht ein wichtiges Konzept: Sogar unendlich viele Schritte können unter Umständen eine endliche Gesamtstrecke ergeben. Wenn jeder Schritt, den Sie tun, halb so groß ist wie der vorangehende, dann misst die insgesamt zurückgelegte Entfernung selbst bei unendlich vielen Schritten das Doppelte der ersten Strecke:

    1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + ... = 2 [...]

Mit Hilfe dieses Paradoxes hat Zenon die Behauptung aufgestellt, dass unter der Voraussetzung einer unendlichen Teilbarkeit von Raum und Zeit Bewegung noch nicht einmal beginnen könne."
(S. 17f)

  1.  

  1. "Wie durch Zauberei treten die irrationalen Zahlen auf, sobald wir versuchen, die Linie der Geometrie mit den Zahlen der Arithmetik in Einklang zu bringen, und zwar dergestalt, dass wir einen Punkt auf einer Linie als einzelne reelle Zahl ansehen. Wir wissen, dass wir in der Lage sein müssten, Zahlen auf einer Geraden unterzubringen, um der Idee Ausdruck zu verleihen, dass zwei Zahlen eine bestimmte Entfernung aufweisen und dass Punkte einander vorangehen, das heißt, dass von zwei Punkten einer zuerst und der andere danach kommt. Wir müssten auch in der Lage sein, zwischen Zahlen und ihrer Darstellung als Punkte auf einer Linie vor und zurückzugehen. Wenn sechs größer ist als vier, müsste sich die Darstellung beider Zahlen auf einer Strecke als nützlich erweisen - wir müssten erkennen können, dass sich die Vier links von der Sechs befindet, und eine anschauliche Vorstellung von der Entfernung zwischen den beiden Zahlen gewinnen.

Bild

Auf der Geraden können wir den Punkten auch Brüche zuordnen. Zwischen 0 und 1 sind Zahlen wie 1/2,1/4,1/5 und so fort, zwischen 1 und 2 Zahlen wie 11/2, 11/4 und so weiter. Andere Zahlen wie 358/719 und ähnliche - alles Brüche - lassen sich ebenso leicht auf der Zahlengeraden bestimmen. Doch die wirkliche Länge, die »Konsistenz«, der Zahlengeraden ergibt sich nicht daraus, dass man alle Zahlen auf ihr zusammendrängt. Selbst bei unendlicher Verdichtung aller Brüche und ganzer Zahlen - aller rationalen Zahlen - auf einem Abschnitt der Zahlengeraden erhielten wir immer noch ein Sieb, das unendlich viele Löcher hätte, und keine durchgehende Linie. Um die wirkliche Textur der Geraden herzustellen, brauchen wir die irrationalen Zahlen. Ohne sie hätten wir nur eine unendliche Ansammlung von Punkten, sehr dicht zwar, aber nicht zusammenhängend - keine Gerade.

[...]

  1. Um zu beweisen, dass die Struktur der Zahlengeraden von den irrationalen und nicht den rationalen Zahlen geliefert wird, verwenden wir ein Argument, das Zenons Paradox ähnelt, nach dem niemand in der Lage ist, ein Zimmer zu verlassen. Wie bekannt, zeigte sich bei der Untersuchung dieses Paradoxes, dass die unendliche Reihe, die entsteht, wenn immer wieder die Hälfte der bis zur Tür verbleibenden Entfernung addiert wird, konvergiert: 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + ... = 2. Das ist eine wichtige Eigenschaft der Summe von geometrischen Reihen.
    Die rationalen Zahlen lassen sich abzählen, obwohl sie unendlich sind (eine Eigenschaft, die Georg Cantor bewiesen hat). Dagegen sind die irrationalen Zahlen so unendlich, dass sie nicht abzählbar sind (eine weitere Eigenschaft, die Cantor bewiesen hat). Schauen wir uns nun alle Zahlen zwischen 0 und 1 an. Die Länge des Intervalls, wenn es intakt ist, wird wiedergegeben durch die Einheit 1 - 0 = 1. Entfernen wir nun alle rationalen Zahlen. In diesem Fall schließen wir jede rationale Zahl in ein winziges Teilintervall ein, so als würden wir einen kleinen Schirm über jeder Zahl aufspannen. Die Größe des Schirms über jeder Zahl nimmt für jede nachfolgende rationale Zahl um die Hälfte ab. Beginnen wir mit einem Schirm der Größe ε (einer beliebig kleinen Zahl wie etwa 0,00000001), ist die Summe der Länge all dieser unendlich vielen winzigen Schirme ε (1 + 1/2 + 1/4 + 1/8  + ...) = 2ε. Da ε beliebig klein war, hat das ursprüngliche Intervall zwischen 0 und 1 also eine unbedeutende Gesamtlänge verloren, sodass es im Wesentlichen immer noch die Länge 1 hat, die es besaß, als noch alle rationalen Zahlen enthalten waren. Wir sagen, die rationalen Zahlen haben das Maß null innerhalb der Zahlengeraden. Das vorstehende Argument ist ein Beispiel für einen mathematischen Beweis.
    Eine Zahl ist entweder rational oder irrational, und die beiden Gruppen sind auf der Geraden unendlich vermischt. Doch wenn alle rationalen Zahlen entfernt werden, bleibt die Gesamtlänge der Geraden unverändert - es gibt unendlich mehr irrationale als rationale Zahlen.

  2. Die [ir!]rationalen Zahlen selbst untergliedern sich in mehrere Gruppen. Zahlen wie die Quadratwurzel von zwei sind zwar irrational und haben endlose, sich nicht wiederholende Dezimalteile, lassen sich aber in gewissem Sinne mathematisch bewältigen. Solche Zahlen heißen algebraische Zahlen, weil sie Wurzeln polynomischer Gleichungen mit rationalen Koeffizienten sind. Die Quadratwurzel von zwei ist beispielsweise eine Wurzel der Gleichung x2 - 2 = 0. Da das ein Polynom mit dem Koeffizienten 1 ist, ist die Wurzel algebraisch. Cantor bewies, dass die Menge der algebraischen Zahlen genauso groß ist wie die Menge der rationalen Zahlen.

  3. Nichtalgebraische irrationale Zahlen heißen transzendente Zahlen. Alle berühmten irrationalen Zahlen wie π und e sind transzendent. Das sind »wirklich irrationale« Zahlen - sie lassen sich nicht zählen, nicht als Wurzeln polynomer Gleichungen (oder in irgendeiner anderen Weise).
    [...]
    Irrationale Zahlen, die nicht algebraisch sind, sind transzendent. Die meisten Zahlen auf der Zahlengeraden sind transzendent. Zwar sind auch algebraische Zahlen und rationale Zahlen unendlich, doch die transzendenten Zahlen sind von einer Unendlichkeit höherer Ordnung. Wenn Sie auf der Zahlengeraden zufällig eine Zahl »wählen    «

[vgl. das "Nadelbeispiel" oben]

könnten, wäre die Zahl mit einer Wahrscheinlichkeit von eins transzendent. Dass man auf eine rationale oder algebraische Zahl stieße, wäre - obwohl es unendlich viele von ihnen gibt - durch das Übergewicht der transzendenten Zahlen einfach zu unwahrscheinlich. Daher ist die Wahrscheinlichkeit null, dass wir, wenn wir zufällig eine Zahl auf der Zahlengeraden bestimmen, eine rationale oder algebraische Zahl erwischen."
(S. 88ff)

  1.  

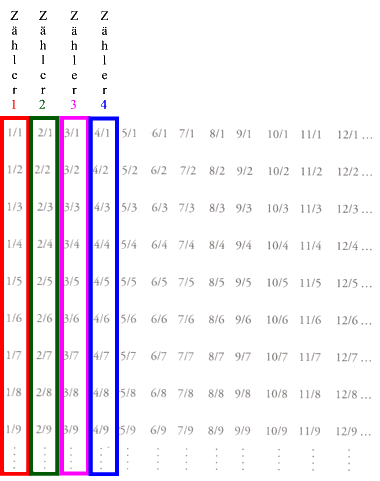
  1. "Die natürlichen Zahlen lassen sich abzählen, obwohl sie unendlich sind. Es kommt auf den Prozess des Abzählens an, nicht auf das tatsächliche Zählen, denn dieses Abzählen würde niemals enden. Die natürlichen Zahlen lassen sich abzählen, weil es möglich ist, sie nacheinander zu nennen: 1, 2, 3, 4 ... und so fort. Die natürlichen Zahlen sind - obwohl unendlich - also abzählbar. Schon am Anfang seiner mathematischen Laufbahn verwendete Cantor ein scharfsinniges Argument, um zu zeigen, dass auch die rationalen Zahlen abzählbar sind. [...] Cantor [zeigt], dass es ebenso viele rationale Zahlen gibt wie ganze Zahlen. Das Argument bezeichnet man als Beweis nach dem Cantor'schen Diagonalverfahren.
    Das erste Mal verwendete Cantor den Beweis 1874, doch später
    , 1891, verbesserte er ihn [...] für diesen Beweis brachte Cantor die rationalen Zahlen zunächst, wie unten abgebildet, in eine zweidimensionale Anordnung.

Bild

Setzt man die Pfeile in der Abbildung wie gezeigt von Zahl zu Zahl fort, entsteht die eindeutige Zuordnung der rationalen Zahlen zu allen natürlichen Zahlen. Hier ist 1/1 gepaart mit 1, 2/1 mit 2, 1/2 mit 3, 1/3 mit 4 und so fort.
So wird jede rationale Zahl gegen eine natürliche Zahl abgezählt (obwohl es Redundanzen gibt, beispielsweise taucht die Zahl 1 in der Gestalt von 2/2, 3/3 usw. auf und wird unendlich viele Male gezählt).
Der Prozess führt zu einem überraschenden Ergebnis. Wwährend die natürlichen Zahlen, oder die ganzen Zahlen - zu denen jetzt auch null und alle negativen ganzen Zahlen gehören -, alle durch eine Einheit voneinander getrennt sind, scheinen die rationalen Zahlen sehr viel zahlreicher zu sein, weil wir wissen, dass sie dichter sind als die ganzen Zahlen. Die rationalen Zahlen sind mathematisch dicht in der Menge der reellen Zahlen, was bedeutet, dass wir in jeder infinitesimalen Nachbarschaft jeder beliebigen Zahl auf der Zahlengeraden rationale Zahlen finden können. Und doch ist der Beweis schlüssig: Ohne Zweifel gibt es ebenso viele rationale Zahlen wie ganze Zahlen. Das Unendliche der ganzen Zahlen und das Unendliche der rationalen Zahlen ist von gleicher Ordnung.
[...]

  1. Kurz vor Weihnachten 1873 gelang ihm der scharfsinnige Beweis, dass die transzendenten Zahlen (oder allgemeiner: die reellen Zahlen, die die transzendenten enthalten) eine Unendlichkeit von so viel höherer Ordnung besitzen, dass sie nicht abzählbar sind.
    Cantor begann - wie in seinem Diagonalverfahren - mit der Annahme, dass es irgendeine Möglichkeit gebe, die Zahlen auf dem Zahlenkontinuum abzuzählen. Dabei schränkte er seine Analyse auf die Zahlen zwischen 0 und 1 ein. Er ging von der Annahme aus, dass sich die reellen Zahlen von 0 bis 1 ihrer Reihenfolge nach auflisten lassen. Dann versuchte er, jede dieser Zahlen mit einer ganzen Zahl zu paaren. Die erste Zahl auf der Liste lässt sich der Zahl Eins zuordnen, die nächste der Zahl Zwei und so fort. Er nahm an, alle Zahlen zwischen 0 und 1 ließen sich auf diese Weise auflisten (hier ohne besondere Ordnung wiedergegeben):

0,1242156743789543...
0,2341176299829547...
0,7763982396546611...
0,4829534479012375...
0,0348109432162984...
..................................
..................................

Cantor betrachtete diese Aufstellung als eine unendliche Liste der unendlich vielen Zahlen zwischen 0 und 1. Doch da machte er eine verblüffende Entdeckung. Er bemerkte, dass er eine Diagonalzahl konstruieren konnte, indem er eine Ziffer von jeder der unendlich vielen Zahlen aus der obigen Liste übernahm. Dazu wählte er die erste Dezimalziffer aus der ersten Zahl der Liste, die zweite aus der zweiten Zahl und so fort ad infinitum. Diese Zahl ist 0,13691...
Jetzt bediente sich Cantor einer sehr klugen Methode. Er veränderte jede Ziffer der Diagonalzahl. Diese Transformation ließ sich beispielsweise dadurch erreichen, dass er zu jeder Ziffer eins addierte, sodass er eine neue Zahl erhielt: 0,24702... Diese neue Zahl ist von allen (unendlich vielen) Zahlen auf der obigen Liste verschieden, weil sie von jeder einzelnen Zahl auf der Liste zumindest in dem Wert der von dieser Zahl übernommenen Ziffer verschieden ist (denn zu dieser Ziffer wurde eins addiert). Da die neue Zahl, die Cantor erzeugt hatte, von allen Zahlen auf der Liste verschieden war, ist es nicht möglich, alle Zahlen zwischen 0 und 1 aufzulisten. Damit war beweisen, dass die Menge aller reellen Zahlen größer ist als die (unendliche) Menge aller ganzen und aller rationalen Zahlen. Wie viel größer die Menge aller reellen Zahlen war als die Menge aller ganzen Zahlen, konnte Cantor allerdings nicht angeben."
(S. 115ff)

So "populärwissenschaftlich" Aczels Buch weitgehend ist, so setzt er mir beim Leser doch oftmals allzu viele mathematische Vorkenntnisse voraus. Das Problem besteht wieder mal darin, welchen Leser sich der Autor vor seinem inneren Auge vorstellt, also üblicherweise "den Menschen mit Abitur" (oder - weil Aczel Amerikaner ist - einem amerikanischen äquivalent).

Aber was weiß dieser hypothetische "Mensch mit Abitur", wenn er nicht gerade Techniker, Naturwissenschaftler oder gar Mathematiker geworden ist, zehn Jahre nach dem Abitur denn noch von der Mathematik (außer reinen Bezeichnungen wie "der Satz des Pythagoras" oder "Dreisatz")?!

(Schon gar nicht sind Aczels rein mathematische Erläuterungen aber für MathematikerInnen gedacht: die unterfordert er, denn die wissen das alles doch schon! Bzw. denen kann er doch nur Neues über das eigentliche Thema seines Buches erzählen, also die kulturellen Hintergründe.)

Nun könnte man ja vielleicht meinen, Aczel setze einfach voraus: "wenn jemand ein mathematisches Buch wie meins liest, wird er schon spezielle mathematische Vorkenntnisse haben." Genau dahinter scheint mir aber ein doppelter Denkfehler zu stecken:

  1. suggeriert der Titel "Die Natur [!] der Unendlichkeit [oder Unendlichkeit der Natur?]" bzw. im amerikanischen Original "The Mystery of Aleph" ja noch keineswegs Mathematik (oder verschweigt sie hinterhältig?), und selbst in den Untertiteln "Mathematik, Kabbala und das Geheimnis des Aleph" bzw. "Mathematics, the Kabbalah and the Search for Infinity" ist die Mathematik nur einer von mehreren "geheimnis"(!)vollen Aspekten. Aczel versucht ganz offensichtlich, auch NichtmathematikerInnen zu ködern;

  2. sollten Bücher mit dem hier vorliegenden "Niveau" bzw. allgemeinkulturellen Anspruch meiner Meinung nach als imaginierte Zielgruppe immer Leute haben, die seit Ewigkeiten keine Mathematik betrieben haben

(durch ihre Berufe davon abgekommen sind oder nach dem typischen Mathematikunterricht in der Schule erst mal für lange Zeit gründlich von Mathematik "die Schnauze voll hatten"),

aber sehr viel später
doch noch bzw. wieder einen Zugang zu ihr finden wollen

(und sei's, dass sie über nichtmathematische "Beilagen" indirekt für die Mathematik geködert werden).

Dann aber kann man von kaum mehr als simpelster Schulmathematik ausgehen.

Manchmal scheint mir Aczel allerdings auch "den" Laien für zu dumm zu halten bzw. zu meinen, ihm nicht allzu viel zumuten zu dürfen

(wobei die Entscheidung, wann etwas nun tatsächlich zu schwierig für Laien ist, ja oftmals nicht leicht und oftmals Ermessenssache ist;

allerdings machen sich viele Autoren diese Entscheidung auch allzu leicht, indem sie [mit dem fatalen Diktum Stephen Hawkings] kritiklos voraussetzen bzw. übernehmen, dass eine mathematische Formel die Zahl der Leser gleich halbiere; nein, man darf [und muss manchmal] durchaus mathematische Formeln verwenden - muss sie dann allerdings erklären und ihren Wert bzw. ihre Unersetzbarkeit aufzeigen).

Solch eine Unterforderung geschieht beispielsweise, wenn Aczel einen wirklich zentralen Punkt seiner Argumentation in 2., nämlich die Abzählbarkeit auch der algebraischen Zahlen,

(anders als bei den rationalen Zahlen in 3.)

nirgends erklärt bzw. beweist, also nur behauptet

(weshalb ein "Kunde" ja immerhin sagen könnte: "genau diesen zentralen Punkt glaube ich nicht, und deshalb bricht für mich hier die gesamte Argumentation zusammen").

Zentral ist dieser Punkt aber, weil Aczel in 2. doch zeigen will, dass

Da reicht es doch beim besten Willen nicht, dass Aczel ausgerechnet bei der Abgrenzung der algebraischen von den transzendenten Zahlen patzt, nämlich

(und für einen Laien spätestens mit den Begriffen "Polynom" und "Wurzel der Gleichung" wohl vollends unverständlich)

andeutet, was algebraische Zahlen eigentlich sind

("Solche Zahlen heißen algebraische Zahlen, weil sie Wurzeln polynomischer Gleichungen mit rationalen Koeffizienten sind. Die Quadratwurzel von zwei ist beispielsweise eine Wurzel der Gleichung x2 - 2 = 0. Da das ein Polynom mit dem Koeffizienten 1 ist, ist die Wurzel algebraisch."),

"Cantor bewies, dass die Menge der algebraischen Zahlen genauso groß ist wie die Menge der rationalen Zahlen."

Wie hat Cantor es denn bewiesen?

Wenn Aczel die Beweisbarkeit aber nur behauptet, geht das über "es gibt algebraische Zahlen und die sind abzählbar, basta!" nicht hinaus. Und ist der Beweis denn wirklich so eindeutig für Laien zu schwierig?

Kommt hinzu, dass sich Aczel den entscheidenden "Gag" entgehen lässt

(wo er doch schon vorher dieses wunderschön aussagekräftige Bild der "Schirmchen" erfunden hat - das ich allerdings noch anschaulicher ausbauen, nämlich um den Regen ergänzen würde):

Die für einen Laien zumutbaren Grenzen würden mir allerdings als bereits überschritten erscheinen, wenn man auch noch beweisen wollte, dass 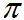Bild und e transzendent sind. für 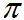Bild tut Aczel das ja immerhin (auf S. 93f) noch ansatzweise, aber eben auch nicht durch vollständigen (überzeugenden) Beweis.

Kleiner Einschub zu Populärwissenschaften: es macht einen gewaltigen Unterschied, ob ein Autor

Ein "guter" populärwissenschaftlicher Autor ist noch nah genug dran an den "Kinderfragen und -einwänden", d.h. er nimmt sie auf und ernst (hat sie noch selbst) und den hypothetischen Leser sozusagen freundschaftlich auf seiner Erkundungsreise "bei der Hand".

Ein populärwissenschaftliches Buch kann und wird natürlich nebenher bzw. ungewollt, weil es wie jedes Buch (also auch jeder Roman) offen ist, zu vielfältigem Nachdenken anregen - und sei's darüber, weshalb es so langweilig oder unverständlich ist

(In Deutschklassenarbeiten gibt es eine unausrottbare Floskel und heißt es oft ausnahmslos pauschal: "der Autor wollte uns zum Nachdenken anregen":

  1. woher weiß man denn, dass er das wollte?

  2. worüber denn und in welche Richtung [was wurde da denn "nachgedacht"]?

  3. mit welchen Mitteln, bzw. wo genau setzte das Nachdenken denn [weshalb] an?

Nebenbei: die - bei SchülerInnen allemal verständliche - Floskel soll wohl signalisieren: "lieber Lehrer, ich habe mir immerhin große Mühe gegeben, den krausen Gedanken des Autors zu folgen - und ausgerechnet diejenige Interpretation zu finden, die Sie in Ihrer unerfindlichen Allmacht für die einzig richtige halten; mehr noch: ich fand das Buch irrwitzig genial [vielleicht verbessert das ja meine Zensur] und habe deshalb mächtig drüber sinniert; und wenn ich nicht gestorben bin, dann nachdenke ich noch heute".)

Aber meiner Meinung nach darf ein Buch nicht (ausdrücklich) zum Nachdenken anregen wollen: ich zumindest bin allergisch dagegen, wenn Autoren mir - sei's ausdrücklich oder (wie bei Aczel) durch offensichtliche Lücken - allzu oberlehrerhaft Aufgaben stellen (und evtl. nicht mal im Anhang die Lösung liefern). Mir scheint dann, sie sind ihrem eigentlichen Auftrag, nämlich mir was zu verklickern, nicht nachgekommen. Und zudem wirkt sowas schnell besserwisserisch bzw. beschämend, wenn man eine gestellte Aufgabe nicht lösen kann; und das insbesondere, wenn es mal wieder heißt, die Lösung sei "trivial einfach".

Angeleitetes Mitdenken erreicht man aber am besten, indem man Ergebnisse nicht einfach fertig hinklatscht, sondern Denkwege vormacht, d.h. den Leser mit auf eine "Denkwanderung" nimmt.
Vor allem aber darf man doch nicht alles fertig hinklatschen, weil dann kein Platz fürs Staunen mehr bleibt: alles wirkt - weil es so einfach ist - allzu selbstverständlich.

Mein Ehrgeiz bzw. meine (einlösbare?) Selbstverpflichtung besteht nun in in dreierlei:

  1. die Lücken aufzufüllen, die Aczel gelassen hat
     (beispielsweise den Beweis, dass die algebraischen Zahlen abzählbar sind),

  2. auf eine Art zu erklären, dass auch ein Laie es zügig verstehen kann
    (ob er am Thema Spaß findet [s.o.], ist dabei eine ganz andere Frage; und doch:)

  3. die latente Spannung, die ich bei Aczels Passagen durchaus empfunden habe, deutlicher herauszuarbeiten, so dass unser hypothetischer Laie vielleicht tatsächlich Geschmack an der Zahlentheorie findet.

In einem ersten Schritt möchte ich Aczels Textauszüge "laienmathematisch" nachbessern (in Anführungszeichen immer die Passagen Aczels):

zu 1., also Zenons Paradoxien:

"Offenbar stießen die Griechen auf die Idee des Unendlichen, weil sie sich lange Zeit erfolglos mit den Paradoxen herumschlugen, die dem Philosophen Zenon von Elea (495-435 v. Chr.) zugeschrieben werden. In dem bekanntesten dieser Paradoxen beschreibt Zenon einen Wettlauf zwischen Achill, dem schnellsten Läufer der Antike, und einer Schildkröte. Da die Schildkröte viel langsamer ist, bekommt sie einen Vorsprung. Nun argumentierte Zenon folgendermaßen: Wenn Achill den Punkt erreicht, von dem die Schildkröte das Wettrennen begonnen hat, ist die Schildkröte ein Stück vorangekommen. Zu dem Zeitpunkt, da Achill diese Strecke zurückgelegt hat, ist die Schildkröte wiederum ein Stück vorangekommen. Und so geht es fort ad infinitum. Also könne der schnelle Achill, so Zenons Schluss, die langsame Schildkröte niemals überholen. Aus diesem Paradox leitete Zenon die Behauptung ab, unter der Voraussetzung, dass Raum und Zeit unendlich teilbar seien, könne es keine Bewegung geben.
Ein anderes Paradox von Zenon, die Dichotomie, besagt, dass Sie das Zimmer, in dem Sie sich gerade befinden, nie verlassen können. Zunächst legen Sie die halbe Entfernung bis zur Tür zurück, dann die Hälfte der restlichen Strecke, dann die Hälfte der Distanz, die Sie nun noch von der Tür trennt, und so fort.
Selbst mit unendlich vielen Schritten - jeder halb so groß wie die vorangehenden - können Sie nie durch die Tür kommen! Hinter diesem Paradox steht ein wichtiges Konzept: Sogar unendlich viele Schritte können unter Umständen eine endliche Gesamtstrecke ergeben. Wenn jeder Schritt, den Sie tun, halb so groß ist wie der vorangehende, dann misst die insgesamt zurückgelegte Entfernung selbst bei unendlich vielen Schritten das Doppelte der ersten Strecke:

    1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + ... = 2 [...]

Mit Hilfe dieses Paradoxes hat Zenon die Behauptung aufgestellt, dass unter der Voraussetzung einer unendlichen Teilbarkeit von Raum und Zeit Bewegung noch nicht einmal beginnen könne."

Warum wird denn in der mathematischen Literatur immer wieder die Achilles-Geschichte aufgewärmt?: weil sie mehr als nur paradox (im Sinne von: zwei gleichberechtigte Wahrheiten widersprechen sich), nämlich sogar vollständig irrsinnig ist. Sie soll ja wohl zeigen, dass der Verstand (die Logik) zu Ergebnissen kommen kann, die jeglicher Alltagserfahrung krass widersprechen. Nur wird dabei vorausgesetzt, dass jeder in dieser logischen Art denken kann - oder aber, wenn er es nicht kann, dumm ist. Bzw. die "Paradoxie" ergibt sich doch überhaupt erst für jemanden, der der Logik folgen will und kann.

Ich wette aber, dass für viele Laien das Problem ganz woanders liegt: sie halten nicht den Widerspruch zur Alltagserfahrung für paradox, sondern schon den logischen Gedankengang selbst. Viele Laien würden wohl sagen: dieser Zenon hatte derart einen "an der Waffel" (oder aber war derart ironisch), dass er die Logik solange ausgerenkt hat, bis völliger Schwachsinn dabei heraus kam. Denn "natürlich überholt Achill irgendwann die Schildkröte, basta! - Wieso also ein an den Haaren herbei gezogenes Beispiel konstruieren, in dem Achilles das widersinnigerweise nicht schafft."

Bzw. schauen wir uns doch mal den letzten Satz der oben zitierten Passage an:

"[...] Zenon hat die Behauptung aufgestellt, dass unter der Voraussetzung einer unendlichen Teilbarkeit von Raum und Zeit Bewegung noch nicht einmal beginnen könne."

Wenn unser Laie eben doch schon ein wenig in mathematischer Logik vorgebildet ist (die eben keineswegs identisch mit der Alltagslogik ist), wird er vielleicht einwenden:

Der minder vorgebildete Laie wird aber vermutlich gar nicht die (sowieso unverstandene) Voraussetzung, sondern nur die "offensichtlich blödsinnige" Folgerung hören - und dann antworten: "das weiß aber doch jeder (so dumm, es nicht zu wissen, konnte nicht mal ein oller Grieche sein), dass in der Welt Bewegungen möglich sind (sonst könnte Zenon nicht mal davon reden) - also was soll der ganze Schwachsinn?!"

Aber setze ich hier nicht vielleicht doch einen allzu unwilligen Leser voraus? Immerhin hat er das Buch (mit dem Untertitelbestandteil "Mathematik") ja schon gekauft, ist er also zu allerlei Gehirnverrenkungen bereit. Ich meine dennoch, dass selbst der gutwilligste und aufgeschlossenste Laie natürlich seinen "gesunden Menschen- bzw. Alltagsverstand" nicht an der Tür abgeben, sondern ihn latent beibehalten wird. Und diesen "Alltagsverstand" sollte man nicht stillschweigend übergehen (bzw. nicht die mathematische Logik stillschweigend voraussetzen), sondern ausdrücklich hervorkitzeln! (... was Aczel beispielsweise mit "können Sie nie durch die Tür kommen" ja immerhin indirekt tut).

Ich sehe insgesamt also die Gefahr, dass die ganze Achilles-Geschichte (sicherlich gegen den Willen des Autors) nur eins bewirken könnte: Zenon (und mit ihm - wie es ja oft geschieht - alle Menschen früherer Zeiten und am Ende auch noch alle Mathematiker) als Idioten darzustellen - und dass der Leser sich "solchem Schwachsinn" verweigert, also die Lektüre abbricht.

Und deshalb meine ich: wenn schon das Achilles- oder das (später
ja noch benötigte) Zimmerbeispiel, dann muss man den Leser bei seinen Bedenken abholen bzw. diese (wie ich es eben bewusst drastisch getan habe) mitformulieren.

Z.B. könnte man eben deutlicher hervorheben:

"Der Philosoph [Zenon] versuchte [...] mit einer ausgezeichneten Kette von Argumenten oder Paradoxa zu Zeit und Raum auf die Täuschung durch die Sinne aufmerksam zu machen. Ein typisches Beispiel für Zenons Paradoxa ist das Beispiel des Wettlaufes Achills mit der Schildkröte, der, wenn er nur die Hälfte des Weges der Schildkröte liefe, diese nicht einholen könne, weil er immer an dem Ort ankomme, den die Schildkröte schon verlassen habe. Mit diesem Beispiel versuchte Zenon, die logische Unmöglichkeit der Bewegung zu erbringen. Die Sinne, so meinte er, machen uns glauben, dass Bewegung existiere. In Wirklichkeit handele es sich dabei um eine Illusion [...]"
 (Microsoft Encarta Professional 2002)

Mir scheint, dass überhaupt erst durch diese philosophische Erklärung (die Außenwelt als Sinnestäuschung) die Achilles-Geschichte verständlich wird: sie ist erstmal "nur" erhellendes Beispiel (in eine Erzählung [!] umgesetzte Philosophie) für etwas, was jeder weiß: dass es Sinnestäuschungen gibt. Ich vermute sogar, dass die allermeisten das schon mal zu Ende gedacht haben: dass die ganze Außenwelt Sinnestäuschung (Erfindung des Ichs bzw. neumodisch "virtuell") sein könnte - eine (nebenbei unwiderlegbare) Einstellung, die man "Solipsismus" nennt

(der Widersprechende könnte ja auch nur eine "Fata Morgana" sein).

Wenn aber die gesamte Außenwelt Sinnestäuschung wäre, dann doch wohl auch jegliche Bewegung! Und dass die Welt stillsteht, hat wohl auch schon jeder mal erfahren, wenn er sich langweilte oder einsam war oder überrascht wurde ("ihm stand vor Schrecken das Herz still").

Solch philosophische Hintergründe schließen ja nicht aus (aber so weit ist der Leser ja noch gar nicht!), dass das Achilles-Beispiel auch innermathematisch produktiv gewirkt hat, und sei's "nur", dass damit - und zwar erstmals, also evtl. mit einem Riesenschrecken - offenbar wurde, dass Mathematik (also der menschliche Geist!) aller primären Anschauung widersprechen bzw. über sie hinaus führen kann.

Mit Zenons Paradox sind wir vermutlich an einem entscheidenden Wendepunkt der Menschheit, nämlich einer beginnenden, manchmal sehr produktiven, manchmal aber auch lähmenden Schizophrenie zwischen Alltagserfahrung einerseits und mathematisch-naturwissenschaftlichem Denken andererseits.

(Vgl. auch

Und das sollte man doch laut sagen statt verschweigen!

Sehr gut finde ich es natürlich, dass Aczel die später
in seiner Argumentation nochmals dringend benötigte Reihe

    1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + ...

anhand einer Geschichte (mit dem Mann, der durch den Raum [!] geht) verdeutlicht.

Aber auch da ist er schon "mathematisch verdorben" (kann er nicht mehr aus seiner mathematischen Haut), wenn er gleichsetzt:

    1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + ... = 2

für den Laien wird das nämlich nie gleich 2 (der Mann erreicht nie vollends die Tür), sondern es (er) nähert sich der 2 (der Tür) zwar unendlich nahe an, erreicht die 2 (die Tür) aber nie. Aczel sagt es ja vorher sogar selbst: "können Sie nie durch die Tür kommen", was ja wohl auch heißt "... niemals bei der Tür an": es ist (fast) wie mit dem Esel, der immer nur einem ihm vorgebundenen Bündel Heu "hinterher" läuft

(mit dem Unterschied, dass es immer gleich weit entfernt bleibt, er sich ihm also nicht mal nähert).

Dass die unendliche Summe 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + ... tatsächlich 2 ergibt, ist ja (auch mathematisch!) keine Tatsache, sondern eine Definition

(MathematikerInnen denken sogar noch krauser

[und es wird nie die enormen Schwierigkeiten von SchülerInneN beim Limesbegriff verstehen, wer sich das nicht klar macht]:

für MathematikerInnen gibt es die 2 sozusagen gar nicht, sondern sie ergibt sich erst als Grenzwert der Summe: die 2 "sei" das, wo die Summe unendlich nah dran geht.
Vgl. etwa:

Vor allem ist das Gleichheitszeichen ja auch für Aczels später
e Argumentation völlig unnötig. Es reicht die umgangssprachliche Formulierung, dass die Summe zwar unendlich nah an 2 heran geht, aber kleiner bleibt:

    1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + ... < 2

"Sie berühren sich im Unendlichen!" - "Wie romantisch!"

Zwar widerspricht dieses < aller mathematischen Konvention (!), ja geradezu allem mathematischen Fortschritt, aber ein populärwissenschaftlicher Autor sollte den Mut haben, von mathematischen Besserwissern und Puristen abzuweichen, wenn Übergenauigkeit nicht sinnvoll ist bzw. an der gerade behandelten Stelle nicht benötigt wird.

(Aber vielleicht bin ich es ja [und ist es nicht Aczel], der hier "mathematisch verdorben" ist, denn schließlich sehe ich hinter dem klitzekleinen Gleichheitszeichen eine ausufernde mathematische Theorie, während der Laie vielleicht gar nicht so genau hinschaut und dieses bisschen "=" einfach überliest bzw. schluckt. Und dennoch: hat er nicht den eigentlichen Gag missverstanden, wenn er - durch das Gleichheitszeichen irregeführt - meint, die 2 bzw. Tür werde tatsächlich erreicht?)

Bei Achilles wie dem Mann in dem Raum könnte noch ein "falscher" Eindruck aufkommen: dass die Logik der Geschichten nur funktioniere, weil beide langsamer würden. In dieser Logik wäre es also zumindest bei Achilles gar kein Wunder, dass er die Schildkröte nie einholt

(vermutlich vergisst Achilles vor lauter Nachdenken über das mathematische Problem das Laufen und wird deshalb immer langsamer: noch so ein lebensunfähiger Philosoph!: 

Bild,
wobei die Thrakerin über Thales lacht, der vor lauter Sterngucken in einen Brunnen fällt).

Sowohl Achilles als auch der Mann in dem Raum schaffen ja nur immer kürzere Wege. Da könnte (zumindest bei Achilles) ergänzt werden: "... aber auch in immer kürzerer Zeit". Die Geschwindigkeit (also Weg durch Zeit) bleibt also immer gleich!

Aber letztlich ist die Geschwindigkeit (insbesondere bei dem Mann in dem Raum) sogar egal: irgendwann erreicht Achilles, egal wie schnell er läuft, tatsächlich genau den Punkt, an dem die Schildkröte gerade vorher noch war, und das sind insgesamt unendlich viele Punkte.

(Womit nebenbei die ganze Zeit implizit Stetigkeit vorausgesetzt wird: weder Achilles noch die Schildkröte überspringen Zwischenräume.)

Und dennoch erreicht er NICHT immer nur Punkte, an denen die Schildkröte schon war, denn irgendwann - wir wissen es ja alle - überholt er sie, lässt sie also hinter sich zurück und erreicht also keine Punkte mehr, an denen die Schildkröte vorher mal war.

Noch etwas stört mich: dass die Paradoxien zwar immer gezeigt, aber nie aufgelöst werden.

(Vgl.: wenn ein Mathematiker mal so richtig witzig oder auch einfach nur besserwisserisch sein will, fragt er die Gäste auf einer Party [wobei er schon - vielleicht fälschlich - einen intuitiven Begriff von Wahrscheinlichkeit voraussetzt], wie hoch wohl die Wahrscheinlichkeit ist, dass mindestens zwei Gäste am selben Tag Geburtstag haben. Jeder wahrscheinlichkeitstheoretisch Unbedarfte [und überhaupt jeder, der genau dieses Beispiel noch nicht kennt!] würde da auf einer durchschnittlichen großen Party wohl auf größte Unwahrscheinlichkeit tippen; oder genauer: auf eine überzeugende Wahrscheinlichkeit erst dann, wenn auf der Party mindestens 365/2, also mehr als 182 Gäste anwesend wären [was aber auf einer üblichen "intimen" Party nicht der Fall ist]. Die so sicher wie das Amen in der Kirche folgende Behauptung des Mathematikers, dass "gleicher Geburtstag" aber "in Wirklichkeit" schon bei nur 23 anwesenden Personen eher wahrscheinlich als unwahrscheinlich sei, bleibt dann aber fast notgedrungen unbegründet im Raum stehen:

Es bleibt also,

Nebenbei: ganz besonders blöde Aufgabenstellungen geben schon den "point of no return", also 23, vor und lassen dann nur bestätigen, dass da die Wahrscheinlichkeit schon größer als 0,5 ist. Mag ja sein, dass für die Behandlung der allgemeinen Fragestellung noch nicht genügend "Mathematik" vorhanden ist, aber dann lasse man das Beispiel doch besser ganz weg.)

"Wieso überholt Achilles die Schildkröte dann aber trotzdem?" Das Problem besteht da allerdings darin, dass man dazu sehr tief in spezielle Gebiete der Mathematik einsteigen müsste - die nicht Aczels Thema sind und sein dürfen: er käme irritierend weit weg von seinem eigentlichen Thema.

(Achilles überholt die Schildkröte ja genau an dem Punkt, an dem er ihr angeblich zwar unendlich nahe kommt, sie aber dennoch nie erreicht.)

(Aczel hätte das Achilles-Beispiel auch ganz weg lassen können, weil er es im Gegensatz zum Zimmer-Beispiel [s.u.] später
nie wieder braucht. Und doch ist das Achilles-Beispiel erheblich eindrücklicher, weil unlogischer als das Zimmer-Beispiel: letzteres borgt also ganz offensichtlich von ersterem "nur" die Dramatik.

In Wirklichkeit sind die beiden Beispiele aber gleichbedeutend bzw. - wie MathematikerInnen sagen würden - "äquivalent":

zu 2a.:

"Wie durch Zauberei treten die irrationalen Zahlen auf, sobald wir versuchen, die Linie der Geometrie mit den Zahlen der Arithmetik in Einklang zu bringen, und zwar dergestalt, dass wir einen Punkt auf einer Linie als einzelne reelle Zahl ansehen. Wir wissen, dass wir in der Lage sein müssten, Zahlen auf einer Geraden unterzubringen, um der Idee Ausdruck zu verleihen, dass zwei Zahlen eine bestimmte Entfernung aufweisen und dass Punkte einander vorangehen, das heißt, dass von zwei Punkten einer zuerst und der andere danach kommt. Wir müssten auch in der Lage sein, zwischen Zahlen und ihrer Darstellung als Punkte auf einer Linie vor und zurückzugehen. Wenn sechs größer ist als vier, müsste sich die Darstellung beider Zahlen auf einer Strecke als nützlich erweisen - wir müssten erkennen können, dass sich die Vier links von der Sechs befindet, und eine anschauliche Vorstellung von der Entfernung zwischen den beiden Zahlen gewinnen.

Bild

Auf der Geraden können wir den Punkten auch Brüche zuordnen. Zwischen 0 und 1 sind Zahlen wie 1/2,1/4,1/5 und so fort, zwischen 1 und 2 Zahlen wie 11/2, 11/4 und so weiter. Andere Zahlen wie 358/719 und ähnliche - alles Brüche - lassen sich ebenso leicht auf der Zahlengeraden bestimmen. Doch die wirkliche Länge, die »Konsistenz«, der Zahlengeraden ergibt sich nicht daraus, dass man alle Zahlen auf ihr zusammendrängt. Selbst bei unendlicher Verdichtung aller Brüche und ganzer Zahlen - aller rationalen Zahlen - auf einem Abschnitt der Zahlengeraden erhielten wir immer noch ein Sieb, das unendlich viele Löcher hätte, und keine durchgehende Linie. Um die wirkliche Textur der Geraden herzustellen, brauchen wir die irrationalen Zahlen. Ohne sie hätten wir nur eine unendliche Ansammlung von Punkten, sehr dicht zwar, aber nicht zusammenhängend - keine Gerade."

Ich wette, einige MathematikerInnen hätten's sogar noch umständlicher sagen können

(schon allein "die Linie der Geometrie mit den Zahlen der Arithmetik in Einklang zu bringen" und das Wort "Textur"!).

Dabei ist es doch so einfach:

(abgesehen von der vielleicht aufkommenden Schwierigkeit, dass -52398 kleiner als 0,00015 ist, ist das auch und gerade für Laien so intuitiv klar [jeder Zollstock "tut" es], dass eine zusätzliche Erklärung fast schon kontraproduktiv wirken muss).

(Vgl. etwa

Im hier vorliegenden Fall:

(Ich würde das nicht mal "geometrisch", sondern schon eher [noch vormathematisch] "handwerklich" nennen: "so dumm kann man gar nicht sein, nicht einen durchgehenden Strich zeichnen zu können" - bzw. es ist im Gegenteil geradezu ausgeschlossen, einen an keiner Stelle "durchgehenden" Strich [eine nirgends stetige Funktion] zu zeichnen.)

(meine Einwände gegen mein eigenes Vorgehen hier habe ich schon selbst; vgl. Bild "Fragen, Fragen, nichts als Fragen".)

Man sollte denken, dass das, was zeichnerisch so einfach ist, auch rechnerisch nicht so große Schwierigkeiten bereiten könnte.

Weit gefehlt!

Denn soviel sei doch schon vorweg verraten: die Überlegungen zu den Zahlen führen in schwindelerregende und gehinrausrenkende mathematische Höhen - und von dort mit der "Kontinuumshypothese" (s.u.) gleich darauf an den mathematischen Abgrund.

Zwischendurch zu 3a.,

weil dort die Abzählbarkeit der rationalen Zahlen bewiesen wird, die Aczel (widersinnigerweise?) im weiteren Verlauf von 2a. schon voraussetzt bzw. erst - eben in 3a. - nachher beweist:

"Die natürlichen Zahlen lassen sich abzählen, obwohl sie unendlich sind. Es kommt auf den Prozess des Abzählens an, nicht auf das tatsächliche Zählen, denn dieses Abzählen würde niemals enden. Die natürlichen Zahlen lassen sich abzählen, weil es möglich ist, sie nacheinander zu nennen: 1, 2, 3, 4 ... und so fort. Die natürlichen Zahlen sind - obwohl unendlich - also abzählbar. Schon am Anfang seiner mathematischen Laufbahn verwendete Cantor ein scharfsinniges Argument, um zu zeigen, dass auch die rationalen Zahlen abzählbar sind. [...] Cantor [zeigt], dass es ebenso viele rationale Zahlen gibt wie ganze Zahlen. Das Argument bezeichnet man als Beweis nach dem Cantor'schen Diagonalverfahren.
Das erste Mal verwendete Cantor den Beweis 1874, doch später
, 1891, verbesserte er ihn [...] für diesen Beweis brachte Cantor die rationalen Zahlen zunächst, wie unten abgebildet, in eine zweidimensionale Anordnung.

Bild

Setzt man die Pfeile in der Abbildung wie gezeigt von Zahl zu Zahl fort, entsteht die eindeutige Zuordnung der rationalen Zahlen zu allen natürlichen Zahlen. Hier ist 1/1 gepaart mit 1, 2/1 mit 2, 1/2 mit 3, 1/3 mit 4 und so fort.
So wird jede rationale Zahl gegen eine natürliche Zahl abgezählt (obwohl es Redundanzen gibt, beispielsweise taucht die Zahl 1 in der Gestalt von 2/2, 3/3 usw. auf und wird unendlich viele Male gezählt).
Der Prozess führt zu einem überraschenden Ergebnis. Wwährend die natürlichen Zahlen, oder die ganzen Zahlen - zu denen jetzt auch null und alle negativen ganzen Zahlen gehören -, alle durch eine Einheit voneinander getrennt sind, scheinen die rationalen Zahlen sehr viel zahlreicher zu sein, weil wir wissen, dass sie dichter sind als die ganzen Zahlen. Die rationalen Zahlen sind mathematisch dicht in der Menge der reellen Zahlen, was bedeutet, dass wir in jeder infinitesimalen Nachbarschaft jeder beliebigen Zahl auf der Zahlengeraden rationale Zahlen finden können. Und doch ist der Beweis schlüssig: Ohne Zweifel gibt es ebenso viele rationale Zahlen wie ganze Zahlen. Das Unendliche der ganzen Zahlen und das Unendliche der rationalen Zahlen ist von gleicher Ordnung."

Manchmal setzt Aczel (wohl betriebsblind) schon allzu viel voraus. So benutzt er beispielsweise zwar immer wieder die Begriffe "aktual" und "potentiell Unendliches", erklärt sie aber nie bzw. vertraut wohl nur darauf, dass sie durch die permanente Benutzung jeweils im Kontext klar werden.

Ich würde ja schon das Abzählen der natürlichen Zahlen genauer erklären, und zwar vor allem deshalb, weil ich dasselbe Konzept später
auch bei den rationalen Zahlen anwenden kann:

1 2 3 4 n
1. natürliche Zahl 2. natürliche Zahl 3. natürliche Zahl 4. natürliche Zahl n-te natürliche Zahl

Die natürlichen Zahlen lassen sich also mit sich selbst abzählen, man zählt die natürlichen Zahlen - und kann sie, was unten noch wichtig wird, hintereinander bzw. untereinander schreiben.

Im Folgenden würde ich das "Diagonalschema"

Bild

keineswegs (wie Aczel) nur unkommentiert hinstellen ("der Leser wird's schon verstehen bzw. seine Struktur selbstständig er- bzw. nacharbeiten"), sondern kommentieren.

Vorweg: ein Bruch ist dadurch definiert, dass sowohl in seinem Zähler als auch in seinem Nenner ausschließlich natürliche (bzw. ganze) Zahlen stehen.

  1. In jeder (nach rechts unendlichen) Zeile stehen alle Brüche mit demselben Nenner (z.B. 4):

Bild

(wobei ich - so weit sind wir ja noch gar nicht - die Pfeile natürlich noch nicht auftauchen lasse)

Und so werden untereinander und zeilenweise sämtliche Nenner abgearbeitet (1, 2, 3, 4 ...):

Bild

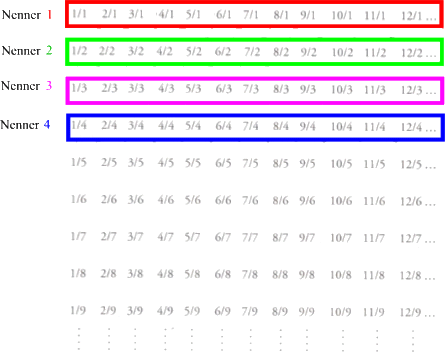
  1. In jeder (nach unten unendlichen) Spalte stehen alle Brüche mit demselben Zähler (z.B. 5):

Bild

Und so werden nebeneinander und spaltenweise sämtliche Zähler abgearbeitet (1, 2, 3, 4 ...):

Bild

  1. aus a. und b. zusammen folgt, dass in dem Schema sämtliche nur denkbaren Brüche erledigt werden

(viele sogar mehrfach, denn z.B. 4/2 = 2/1; oder genauer: zu jedem Bruch tauchen auch all seine Erweiterungen, also unendlich viele gleichwertige [dieselbe rationale Zahl bedeutende], nur verschieden aussehende Brüche auf;
wir zählen unten also viel zu viele Brüche ab; aber wenn uns sogar das gelingt, sind natürlich auch weniger Brüche abzählbar: wenn man die überflüssigen Brüche weglässt, rutschen die restlichen nur in der [abzählbaren] Reihenfolge weiter nach vorne).

Wenn man's erst mal hat (hier sieht), kommt einem diese Anordnung der Brüche so einfach, ja fast naturgegeben vor. Aber erst mal drauf kommen! - und es dann wie unten beim "Schlängelverfahren" nutzen können! Immerhin wäre die hier vorliegende Anordnung zwar schön, aber völlig witzlos, wenn Cantor sie nicht mit dem unten dargestellten "Schlängelverfahren" hätte abzählen können.

Jetzt aber kommt überhaupt erst Cantors entscheidender, und zwar genial einfacher Schritt. Dazu müssen wir uns das Problem klar machen: um alle Brüche abzählen zu können

(wenn das überhaupt geht, und genau das hat er vermutlich probeweise mal angenommen, konnte er ja noch gar nicht sicher wissen),

muss er mit irgendeinem Verfahren sämtliche Brüche (aller Zeilen und aller Spalten) genauso wie die natürlichen Zahlen hinter- bzw. untereinander schreiben können:

Nur kommt man (auch hier) auf diese Weise schon in einer einzigen (beliebigen) Zeile nie ans Ende, weil schon allein in jeder Einzelzeile unendlich viele Brüche stehen. So zählt man sich in einer einzigen Zeile dumm und dämlich - und kommt nie in eine andere Zeile (geschweige denn in die unendlich vielen anderen Zeilen).

Nur kommt man auf diese Weise schon in einer einzigen (beliebigen) Spalte nie ans Ende, weil schon allein in jeder Einzelspalte unendlich viele Brüche stehen. So zählt man sich in einer einzigen Spalte dumm und dämlich - und kommt nie in eine andere Spalte (geschweige denn in die unendlich vielen anderen Spalten).

(nochmals: im Nachhinein, wenn man es erstmal hat bzw. - wie hier - vorgemacht bekommt und fertig sieht, erscheint es so selbstverständlich:

Dennoch: ich vermute, dass ich da nie drauf gekommen wäre - und kann neidlos das Genie Cantor bewundern!):

Bild

usw. usf. bis eben (aber jetzt erst!) zum Gesamtschema

Bild

(Vgl. auch und  ) 

Durch das systematische "Geschlängel" abwechselnd durch Zeilen und Spalten, vor allem aber entlang der Diagonalen "ribbelt" Cantor also sukzessive alle Brüche (in allen Zeilen und allen Spalten) auf und - das ja eben ist Abzählen - stellt sie hübsch einen hinter (bzw. im Folgenden unter) den anderen (vgl. den oben mit den roten Pfeilen "gegangenen Weg"):

(Wichtig dabei ist das systematische Vorgehen: es werden nacheinander alle Diagonalen und damit alle Brüche abgehakt.)

Die (sämtliche!) Brüche lassen sich also - worüber man gar nicht genug staunen kann! - mittels der natürlichen Zahlen abzählen, zu jeder natürlichen Zahl gibt es einen passenden Bruch.

(Genau genommen werden bei Cantors Verfahren viele Brüche sogar mehrfach [unendlich oft] gezählt, nämlich auch Erweiterungen einfacherer Brüche, also z.B. 2/1, 4/2, 6/3 ... Aber die erneuten Nennungen kann man beim Abzählen ja einfach überspringen und danach weiterzählen, als wäre nichts gewesen.)

Damit ist erst mal (schon erstaunlich genug!) die Abzählbarkeit der Brüche bewiesen.

Viel erstaunlicher ist aber:

  • wenn

    • sich jeder natürlichen Zahl genau ein Bruch zuordnen lässt

    • und damit alle Brüche "abgegrast" werden können,

  • dann gibt es gleich viele (!!!) natürliche Zahlen einerseits und Brüche andererseits,

obwohl wir doch wissen, dass es viel mehr Brüche als natürliche Zahlen gibt

(Nebenbei: weil wir oben gesehen hatten, dass gleichwertige Brüche mehrfach [sogar unendlich oft] mitgezählt werden, könnte man sogar meinen, es gebe weniger [gekürzte] Brüche als natürliche Zahlen.)

Der Kasus knaxus dabei ist:

Wie kann das sein: "viel mehr" und doch gleichzeitig "genauso viel"???

(Wenn das einem das Gehirn ausrenkt und man mit Faust sagt:

"Die Botschaft hör ich wohl [der Beweis ist durchaus schlüssig],
 allein mir fehlt der Glaube",

so muss man sich dessen keineswegs schämen

["ich bin halt dumm, aber »richtige« MathematikerInnen werden's wohl verstanden haben"].

Sondern vielen MathematikerInneN ist es nur durch Gewohnheit allzu selbstverständlich geworden, sie können nicht mehr staunen und haben somit - laut Albert Einstein - längst tote Augen. Sie sind zu reinen Technikern "verkommen".

Sogar oder gerade Cantor selbst hat es ja nicht fassen können:

"Ich sehe es wohl, aber ich glaube es nicht."

Mehr noch: mag sein, dass Cantor hinterher "verrückt" geworden ist und sich als Handlungsreisender Gottes in Sachen Unendlichkeit gesehen hat. Aber ich finde es doch immerhin verständlich, dass er beispielsweise das "Diagonalverfahren" als eine überirdische Gottesgabe empfunden hat, nämlich in dessen Entdeckung keinerlei eigenes Verdienst sehen konnte, weil es ja all seiner eigenen Anschauung widersprach.

Aczel weist zudem darauf hin, dass Cantor - wie auch sein Nachfolger im Geiste Gödel - regelmäßig genau dann Wahnsinnsanfälle bekommen hat, wenn er sich mit speziellen Aspekten der Unendlichkeit beschäftigte. Vielleicht wollte "Gott" also nicht, dass man ihm ins Handwerk pfuschte, und strafte deshalb jeden, der es versuchte, mit Wahnsinn.

Falls Sie sich also mit der Unendlichkeit beschäftigen wollen: Ich übernehme keine Gewähr für Ihren Geisteszustand!)

Bei der Betrachtung der Unendlichkeit bzw. dem Vergleich zweier unendlicher (unterschiedlich großer?) Mengen setzt also unsere gesamte gewohnte Logik aus.

Kann man überhaupt von "unterschiedlich groß" sprechen, wenn jede der Vergleichsmengen schon unendlich groß ist???

Gibt es "unendlichER" als "unendlich", also Rangfolgen der Unendlichkeit???

(Etwa so, wie es ja sogar im Himmel unter den unendlichen Heerscharen der Engel noch eine Rangfolge der Cherubim und Seraphim gibt?:


Bild
 [Gustave Doré]

- und Cantor war ja tatsächlich ein sehr religiöser Mensch.)

Genau diese Frage nach der Rangfolge der Unendlichkeit(en)

(gibt es sie, und wenn ja, in welchem Verhältnis stehen die verschiedenen Unendlichkeiten zueinander? Vgl. insbesondere Cantors weltberühmte "Kontinuumshypothese" [s.u.])

war ja Cantors Zentralthema!!!

Bemerkenswert daran ist doch insbesondere, dass die zugrundeliegenden Überlegungen wie insbesondere Cantors "Diagonalverfahren" sehr (genial!) einfach sind und dennoch (oder gerade deswegen?) an die Grenzen des mathematischen Kosmos führen.

Die Gehirnausrenkung ist aber doch gerade der Gag der ganzen Sache: das Thema wird doch nicht nur wegen der rein sachlichen Erkenntnis (Abzählbarkeit rationaler Zahlen) ausgestellt, sondern auch und vor allem wegen der Gehirnausrenkung. Da fände ich es (wie schon oben beim Geburtstagsproblem) doch nur unfair (und zudem undramatisch), diese Verrenkung unter den Tisch zu kehren und so zu tun, als ob sie nur andere ("dumme Laien") erwische.

Die Abzählbarkeit der rationalen Zahlen ist ein Musterbeispiel dafür, dass die Mathematik

(und zwar zum Staunen auch der MathematikerInnen!; oder vielleicht ist das sogar der eigentliche Grund, weshalb sie sie betreiben)

über die menschliche Anschaulichkeit hinausgreifen kann (vgl. Bild ) - wobei sich die Schizophrenie ergibt, dass das

("die Welt ist größer und schöner als das bisschen menschliche Erkenntnis": immerhin ja auch eine Befreiung!)

oder sogar beschämen kann

(die Werkzeuge sind schlauer als ihr Erfinder, sie wachsen ihm über den Kopf - und ihre Ergebnisse gehen  ihn nichts mehr an, befremden ihn nur noch),

Eine ganz andere (für eineN MathematikerIn unsinnige bzw. einfach nur schnöde) Frage ist, "was man von all dem hat". Anwendbar ist es nicht - was das Beste ist, was man über Mathematik und Kunst sagen kann.

(Bei meiner Vorgehensweise sieht man nun endlich mal einen echten Vorteil des Computers gegenüber einem [Aczels] Buch: mit dem Computer lässt sich ein langsames Nacheinander-Entstehen viel einfacher und sogar besser [nämlich in einem Bild] zeigen bzw. lassen sich die Einzelstationen regelrecht nacheinander "abgehen". Dennoch hätte - so meine ich - Aczel nicht ganz auf dieses Nacheinander [mehrerer Zeichnungen] verzichten sollen.
Akkerdings kann man sich auch hier natürlich wieder streiten, ob mein Aufwand Aczels Buch nicht - wieder mal - allzu dick gemacht hätte. Mir scheint aber, das Diagonalverfahren

[als Einführung in die Abzählbarkeit der Brüche, aber auch in das merkwürdige Verhalten unendlicher Mengen]

ist in seinem Buch von so zentraler Bedeutung, dass er sich dafür mehr Zeit und Platz hätte nehmen müssen.)

Zu 2b:

"Um zu beweisen, dass die Struktur der Zahlengeraden von den irrationalen und nicht den rationalen Zahlen geliefert wird, verwenden wir ein Argument, das Zenons Paradox ähnelt, nach dem niemand in der Lage ist, ein Zimmer zu verlassen. Wie bekannt, zeigte sich bei der Untersuchung dieses Paradoxes, dass die unendliche Reihe, die entsteht, wenn immer wieder die Hälfte der bis zur Tür verbleibenden Entfernung addiert wird, konvergiert: 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + ... = 2. Das ist eine wichtige Eigenschaft der Summe von geometrischen Reihen.
Die rationalen Zahlen lassen sich abzählen, obwohl sie unendlich sind (eine Eigenschaft, die Georg Cantor bewiesen hat). Dagegen sind die irrationalen Zahlen so unendlich, dass sie nicht abzählbar sind (eine weitere Eigenschaft, die Cantor bewiesen hat). Schauen wir uns nun alle Zahlen zwischen 0 und 1 an. Die Länge des Intervalls, wenn es intakt ist, wird wiedergegeben durch die Einheit 1 - 0 = 1. Entfernen wir nun alle rationalen Zahlen. In diesem Fall schließen wir jede rationale Zahl in ein winziges Teilintervall ein, so als würden wir einen kleinen Schirm über jeder Zahl aufspannen. Die Größe des Schirms über jeder Zahl nimmt für jede nachfolgende rationale Zahl um die Hälfte ab. Beginnen wir mit einem Schirm der Größe ε (einer beliebig kleinen Zahl wie etwa 0,00000001), ist die Summe der Länge all dieser unendlich vielen winzigen Schirme ε (1 + 1/2 + 1/4 + 1/8  + ...) = 2ε. Da ε beliebig klein war, hat das ursprüngliche Intervall zwischen 0 und 1 also eine unbedeutende Gesamtlänge verloren, sodass es im Wesentlichen immer noch die Länge 1 hat, die es besaß, als noch alle rationalen Zahlen enthalten waren. Wir sagen, die rationalen Zahlen haben das Maß null innerhalb der Zahlengeraden. Das vorstehende Argument ist ein Beispiel für einen mathematischen Beweis.
Eine Zahl ist entweder rational oder irrational, und die beiden Gruppen sind auf der Geraden unendlich vermischt. Doch wenn alle rationalen Zahlen entfernt werden, bleibt die Gesamtlänge der Geraden unverändert - es gibt unendlich mehr irrationale als rationale Zahlen."

Oben war gezeigt worden:

  1. die rationalen Zahlen sind abzählbar, d.h. es gibt

  1.            1     + 1/2     + 1/4     + 1/8     + 1/16    + 1/32      + 1/64   + ...         < 2

Nun sei ε irgendein (!) Schirmdurchmesser.

Dann gilt erst mal rein mathematisch
(indem wir die Gleichung auf beiden Seiten mit εmultiplizieren):

         (1     + 1/2     + 1/4     + 1/8     + 1/16    + 1/32      + 1/64    + ...) ● ε < 2●ε

Bild    1●ε + 1/2●ε + 1/4●ε + 1/8●ε + 1/16●ε + 1/32●ε + 1/64●ε + ...        < 2●ε

Nun errichten wir über jeder rationalen Zahl einen "Schirm", und zwar der Reihe nach immer kleinere bzw. jeweils (im Vergleich mit dem Vorgänger) halb so große:

Nun gilt für all diese Schirme zusammen (wenn man sie also wie oben aufaddiert), dass sie < 2 ● ε sind, d.h. es wird insgesamt eine "Fläche" von < 2 ● ε vor Regen geschützt - der Rest (zwischen minus Unendlich und plus unendlich) wird "nass".

Weil wir gesagt hatten, ε sei irgendein (!) Schirmdurchmesser, können wir ε beliebig klein wählen

(denn eine einzelne Zahl hat allemal immer darunter Platz),

also z.B.:

Wir können also dafür sorgen, dass alle Schirme zusammen unendlich klein werden - dass also fast alles (der Rest) "nass" wird.

Man kann sich das etwa so vorstellen: bei einem regnerischen Fußballspiel sitzen im Stadion

Es sind nur sehr wenige Bayern-Fans (rationale Zahlen) angereist, d.h. die allermeisten anderen, also Borussia-Fans (irrationalen Zahlen) werden nass:

(Hier könnte allerdings ein Denkfehler vorliegen [s.u.]: dass wenige Bayern-Fans [rationale Zahlen] anwesend sind, bedeutet nicht automatisch, dass viele Borussia-Fans [irrationale Zahlen] vorhanden sind: das Stadion [bzw. der Zahlenstrahl] könnte ansonsten weitgehend oder sogar ganz leer sein.)

Nun endlich wird die Antwort auf die "Nadelaufgabe" deutlich: wenn ich mit meiner ultraspitzen Nadel auf den Zahlenstrahl piekse, ist es äußerst unwahrscheinlich, dass ich damit eine rationale Zahl (einen Bayern-Fan) erwische.

Auch das finde ich wieder extrem gehirnausrenkend:

Im Folgenden schauen wir uns nun also den Rest, d.h. die irrationalen Zahlen bzw. Borussia-Fans an:

Zu 2c.:

"Die [ir!]rationalen Zahlen selbst untergliedern sich in mehrere Gruppen. Zahlen wie die Quadratwurzel von zwei sind zwar irrational und haben endlose, sich nicht wiederholende Dezimalteile, lassen sich aber in gewissem Sinne mathematisch bewältigen. Solche Zahlen heißen algebraische Zahlen, weil sie Wurzeln polynomischer Gleichungen mit rationalen Koeffizienten sind. Die Quadratwurzel von zwei ist beispielsweise eine Wurzel der Gleichung x2 - 2 = 0. Da das ein Polynom mit dem Koeffizienten 1 ist, ist die Wurzel algebraisch. Cantor bewies, dass die Menge der algebraischen Zahlen genauso groß ist wie die Menge der rationalen Zahlen."

Auf unser Fussballbeispiel übertragen: die Borussia-Fans (irrationalen Zahlen) lassen sich nun aber ihrerseits wieder in zwei Gruppen unterteilen, nämlich

Der letzte Satz aus dem Aczel-Zitat oben, also

"Cantor bewies, dass die Menge der algebraischen Zahlen genauso groß ist wie die Menge der rationalen Zahlen",

besagt nun,

Wenn das stimmt, heißt das: auch der Anteil der weiblichen Borussia-Fans (algebraischen Zahlen) ist - wie der der Bayern-Fans (rationalen Zahlen) - wieder verschwindend gering

(man könnte auf die weiblichen Borussia-Fans [algebraischen Zahlen] wieder das Schirmbeispiel anwenden),

Cantors Beweis dafür, dass auch die algebraischen Zahlen abzählbar sind, bleibt Aczel allerdings (auch im weiteren Buch) schuldig. Vermutlich hat er sich gedacht, dass dieser Beweis nun wahrhaft Laien überfordert. Genau das will ich aber überprüfen: lässt er sich nicht doch auch verständlich führen?

Vorweg sei ausgehend von der Definition

"Solche Zahlen heißen algebraische Zahlen, weil sie Wurzeln polynomischer Gleichungen mit rationalen Koeffizienten sind."

bei Aczel genauer geklärt, was algebraische Zahlen eigentlich sind.

"Algebraisch werden all jene Zahlen genannt, die als "Wurzeln polynomischer Gleichungen" herauskommen können.

für den Laien irritierend ist da nämlich zweierlei:

  1. wird er nicht (mehr) wissen, was "polynomische Gleichungen" sind
     (und Aczel erklärt es ja auch nirgends genauer: das einzige Beispiel x2 - 2 = 0 bleibt ja ein Spezialfall, an der die Struktur aller "polynomischen Gleichungen" nicht klar wird).

Eine polynomische Gleichung sieht grundsätzlich folgendermaßen aus
 (wobei ich weitgehend die Schreibweise aus unten vorgestelltem Beweis übernehme, nur dass ich die Indizes der Koeffizienten unten dran schreibe):

p(x) = a0 + a1x + a2x2 + ... + amxm .

Aczel spricht von "polynomischen Gleichungen", weil darin ein Gleichheitszeichen vorkommt.

(Oft werden polynomische Gleichungen auch "algebraische Gleichungen", was besser zu ihren Lösungen [um die es hier ja vor allem geht!], nämlich den algebraischen Zahlen, passt.)

In einem Beweis weiter unten kommt hingegen das Wort "Polynom" vor, womit nur der rechte Gesamtterm a0 + a1x + a2x2 + ... + amxm gemeint ist. Eine "polynomische Gleichung" besteht also unter anderem (rechts) aus einem Polynom.

"Polynom" heißt ein Term der Form a0 + a1x + a2x2 + ... + amxm aber, weil da viele (= poly) Summanden (= Nomen) aufaddiert werden.

Dabei gilt:

p(x) = -3 + 17 x - 43 x2 + ... + 509 xm

p(x) = -3 + 17 x - 43 x2 + ... + 509 x4

(eine sogenannte polynomische Gleichung vierten Grades; und entsprechend ergäbe sich für m = 1000 eine polynomische Gleichung 1000. Grades)

Die Summanden sind nach der (aufsteigenden) Größe der Exponenten sortiert, und bis zum höchsten Exponenten können an der Pünktchen-Stelle alle Zwischensummanden vorkommen, im soeben genannten Fall also z.B.

p(x) = -3 + 17 x - 43 x2 + 18x3 + 509 x4

p(x) = -3 + 17    x - 43    x2 + ... + 509     xm

p(5) = -3 + 17 ● 5 - 43 ● x2 + ... + 509 ● 5m

Am Beispiel von

p(x) = -3 + 17    x - 43     x2 + 18      x3   + 509     x4  ergibt sich also für x = 5:

p(5) = -3 + 17 ● 5 - 43 ● x2 + 18 ●  53   + 509 ● 54   =

       = -3 + 17 ● 5 - 43 ● 25 + 18 ● 125  + 509 ● 625 =

       = -3 +     85   -    1075  +    2250      +  318125    =

       =                               319382

Oder kurz: im Spezialfall der polynomischen Gleichung   

p(x) = -3 + 17    x - 43     x2 + 18      x3   + 509     x4 :

ergibt sich für x = 5 der zugehörige Funktionswert p(5) = 319382

(und für ein anders gewähltes x natürlich ein anderer Funktionswert p(x)).

Gemeint damit sind die möglichen Lösungen x, wenn man p(x) vorgibt. Angenommen also mal, in der Gleichung

p(x) = -3 + 17    x - 43     x2 + 18      x3   + 509     x4

ist p(x) = 19, womit sich die Frage ergibt, ob und für welche x die Gleichung

19 = -3 + 17    x - 43     x2 + 18      x3   + 509     x4

lösbar ist.

Nehmen wir also mal den von Aczel gewählten, besonders einfachen Spezialfall

x2 - 2 = 0.

Als erstes übersetzen wir den linken Term x2 - 2 in die übliche Polynomform (zweiten Grades, weil der höchste Exponent 2 ist):

                            a0 + a1   x + a2   x2

x2 - 2 = - 2 + x2 = -2 +  0 ● x + 1 ●x2

Es ergibt sich also die polynomische Gleichung

                 p(x) = -2 +  0 ● x + 1 ●x2

Nun setzen wir noch p(x) = 0, womit sich als neue Form von x2 - 2 = 0 ergibt:

                 0 = -2 +  0 ● x + 1 ●x2

Gesucht sind nun diejenigen x, für die diese polynomische Gleichung lösbar ist.

Dazu gehen wir vorerst mal wieder zur einfacheren Anfangsform x2 - 2 = 0 zurück:

       x2 - 2 = 0  |+2

<=> x2      = 2  | √

<=> x =  Bild  oder  x = - Bild

x =  Bild  bzw.  x = - Bild sind also auch die Lösungen der polynomischen Gleichung

0 = -2 +  0 ● x + 1 ●x2

Und weil in diesem einfachen Beispiel die Lösungen Wurzeln sind, sprechen MathematikerInnen bei den Lösungen aller polynomischen Gleichungen von "Wurzeln".

Nun kann man sich natürlich fragen, weshalb diese polynomischen Gleichungen und ihre Lösungen bzw. "Wurzeln" (also die algebraischen Zahlen) überhaupt so interessant sein sollen

(vgl.: wieso sollten unter allen Borussia-Fans die weiblichen Borussia-Fans von besonderem Interesse sein?).

Der Grund ist ein ganz einfacher (von Aczel an anderer Stelle angedeuteter):

Zum Beweis, dass (auch) die algebraischen Zahlen abzählbar sind, greife ich auf eine andere Quelle, nämlich Bild , zurück:

"Betrachte alle Polynome mit ganzzahligen Koeffizienten. Jedem Polynom kann man eine natürliche Zahl zuordnen, indem man

p(x) = a(0) + a(1)x + a(2)x2 + ... + a(m)xm

die Summe der Absolutbeträge von (n+1)*a(n) zuordnet.
Beispiel: Zum Polynom 2 - x + 3x2 erhält man 1*2 + 2*1 + 3*3 = 13.
Zu jeder natürlichen Zahl gibt es nur endlich viele Polynome, denen die gleiche Zahl zugeordnet wird, denn ein Polynom mit einem gegebenen Wert (z.B. 13) kann keinen Koeffizienten haben, der größer als 13 ist, und der Grad des Polynoms kann auch nicht größer als 13 sein.
 [Wenn ein Polynom einen Koeffizienten gleich 14 hat, oder wenn wenn der Grad eines Polynoms gleich 14 ist, dann wird diesem Polynom mindestens die Zahl 14 zugeordnet.]
Jedes von den nur endlich vielen Polynomen zu einer festen natürlichen Zahl hat nur endlich viele Nullstellen. Folglich können die algebraischen Zahlen abgezählt werden. Die Zählung erfolgt im Prinzip nach der gleichen Methode, mit der Cantor schon die rationalen Zahlen abgezählt (numeriert) hat [...]
Ergo: Die Menge der algebraischen Zahlen ist abzählbar."

Dieser Beweis soll nur besser veranschaulicht werden

(wobei ich die Schreibweise           p(x) = a(0) + a(1)x + a(2)x2 + ... + a(m)xm
in die oben gewählte Schreibweise p(x) =  a0   + a1  x +   a2 x2  + ... +  am xm  übersetze,
also die Indizes nach unten stelle).

übernehmen wir aus dem Beweis als erstes Beispiel das Polynom

                                                                2 -      x + 3x2,

in der oben gewählten Schreibweise also

                                                                2 - 1 ● x + 3x2

Dem Polynom 2 - 1 ● x + 3x2 wird nun folgendermaßen eine natürliche Zahl zugewiesen:

       1                  ●                                   2                                       = 2,

               2               ●                                                          (+1) = 2

                3             ●                                    3                                       = 9

(wobei das im Beweis gewählte Beispiel ungünstig, da missverständlich ist: natürlich muss im dritten Summanden nicht unbedingt der Koeffizient 3 stehen)

Oder kurz: dem Polynom 2 - 1 ● x + 3x2 wird die natürliche Zahl 13 zugeordnet.

Man könnte auch sagen: ihre ganz persönliche Eigenart ist 13.

p(x) =  a0   + a1  x +   a2 x2  + ... +  am xm

ein natürliches Zwischenergebnis nach dem Schema "Platznummer des Koeffizienten mal Absolutbetrag des Koeffizienten" zuordnen.

Z.B. ergibt sich zum Summanden am xm als Zwischenergebnis die natürliche Zahl (m-1) ● | a m |

(wobei man allerdings beachten muss, dass die Platznummer immer um 1 höher ist als der Exponent bzw. zugehörige Index, denn wir beginnen mit a0 auf dem ersten Platz).

Und somit kann man auch jedem Polynom

a0   + a1  x +   a2 x2  + ... +  am xm

eine natürliche Zahl als Endergebnis (Summe der Zwischenergebnisse) zuordnen.

(vgl. zwei Menschen haben beide die persönliche Eigenart, rothaarig zu sein).

Z.B. können verschiedene Polynome dasselbe Endergebnis 13 haben:

"denn ein Polynom mit einem gegebenen [Endergebnis] (z.B. 13)

  1. kann keinen Koeffizienten haben, der größer als 13 ist, und

  2. der Grad des Polynoms kann auch nicht größer als 13 sein":

 "Platznummer des Koeffizienten mal Absolutbetrag des Koeffizienten"

           ≥ 1                                      ●                   > 13

ergäbe sich damit als Zwischenergebnis eine Zahl > 1 ● 13 = 13, und somit wäre auch das Endergebnis > 13
(denn durch die anderen Summanden auf vorhergehenden Plätzen kämen nur weitere positive Zwischenergebnisse hinzu).

Dann würde als 15. Summand im Polynom a14x14 auftauchen

(es sei daran erinnert: die Platznummer ist immer um 1 größer als der Exponent bzw. zugehörige Index),

wobei a14 ≠ 0 sein müsste, den sonst hätte das Polynom ja doch einen niedrigeren Grad. Da für die Koeffizienten vorausgesetzt wurde, dass sie ganzzahlig sind, müsste also gelten: |a14| ≥ 1

Nach der Regel

 "Platznummer des Koeffizienten mal Absolutbetrag des Koeffizienten"

           15                                    ●               |a14| ≥ 1

ergäbe sich damit ein Zwischenergebnis eine Zahl ≥ 1 ● 15 = 15, und somit wäre auch das Endergebnis ≥ 15, also insbesondere > 13
(denn wieder: durch die anderen Summanden auf vorhergehenden Plätzen kämen nur weitere positive Zwischenergebnisse hinzu).

(der Beweis dieses "Fundamental[!]satzes der Algebra" wird hier nicht geliefert, weil er zu weit vom Thema Unendlichkeit abführen würde),

so ergibt sich:

  1. jeder natürlichen Zahl lässt sich eine endliche Zahl von Polynomen und damit polynomische Gleichungen zuordnen,

  2. jede einzelne polynomische Gleichung hat nur endlich viele (algebraische) "Wurzeln",

  3. also lässt sich jeder natürlichen Zahl eine endliche Zahl von (algebraischen) "Wurzeln" zuordnen.

  Anzahl der Gleichungen mit dem Endergebnis 1 Anzahl der Gleichungen mit dem Endergebnis 2 Anzahl der Gleichungen mit dem Endergebnis 3 ...
Anzahl der Gleichungen mit einer Lösung        
Anzahl der Gleichungen mit zwei Lösungen        
Anzahl der Gleichungen mit drei Lösungen        
...        

In jedem der grauen Kästchen taucht dabei eine (endliche) natürliche Zahl auf
(weil ja die endliche Anzahl entsprechender Gleichungen gezählt wird).

Dieses Schema lässt sich aber wieder nach dem Cantorschen "Diagonalverfahren" (s.o.) abzählen, d.h.

die Menge aller "Wurzeln" sämtlicher polynomischen Gleichungen und damit die Menge aller algebraischen Zahlen ist (auch wieder) abzählbar.

Bleibt also nur die Beschäftigung mit dem "Rest vom Rest", d.h.

Nun wäre es ja denkbar oder liegt es inzwischen sogar fast nahe, dass auch diese transzendenten Zahlen (und vielleicht alle Zahlgruppen?) abzählbar sind.

Da muss man sich sofort die Konsequenz (anhand des Schirmchenbeispiels) klar machen:

Umgekehrt: angenommen, wir könnten beweisen (was gleich auch geschehen soll), dass die transzendenten Zahlen nicht abzählbar bzw. "überabzählbar" sind. Dann sind sie zwar mehr als die natürlichen bzw. rationalen bzw. algebraischen Zahlen. Aber das beweist noch lange nicht, dass sie allein dann endlich ausreichen, um den Zahlenstrahl (das Stadion) vollständig aufzufüllen. Es könnte noch immer "Außerirdische" bzw. Lücken geben.

Diese "letzte" Frage soll hier nicht gelöst werden: sie ist Inhalt der cantorschen Kontinuums(!)hypothese, die bis heute unbewiesen ist, ja - wie eben Gödel und Cohen gezeigt haben - im Rahmen der bisherigen Mathematik auch gar nicht beweisbar, aber auch nicht widerlegbar ist - womit wir nun wahrhaft am Rande des mathematischen Kosmos (oder mittendrin, nämlich an seinen durchaus wackeligen "Grundwahrheiten") sind.

(Aczel an das an anderer Stelle ausführlich darstellt, wobei allerdings Gödels und Cohens Beweise nun wahrhaft nicht mehr populärwissenschaftlich darstellbar sind.)

Zu 3b,

also dem Beweis, dass die transzendenten Zahlen "mehr", nämlich nicht abzählbar bzw. "überabzählbar" sind:

"Kurz vor Weihnachten 1873 gelang [Cantor] der scharfsinnige Beweis, dass die transzendenten Zahlen (oder allgemeiner: die reellen Zahlen, die die transzendenten enthalten) eine Unendlichkeit von so viel höherer Ordnung besitzen, dass sie nicht abzählbar sind.
Cantor begann - wie in seinem Diagonalverfahren - mit der Annahme, dass es irgendeine Möglichkeit gebe, die Zahlen auf dem Zahlenkontinuum abzuzählen. Dabei schränkte er seine Analyse auf die Zahlen zwischen 0 und 1 ein. Er ging von der Annahme aus, dass sich die reellen Zahlen von 0 bis 1 ihrer Reihenfolge nach auflisten lassen. Dann versuchte er, jede dieser Zahlen mit einer ganzen Zahl zu paaren. Die erste Zahl auf der Liste lässt sich der Zahl Eins zuordnen, die nächste der Zahl Zwei und so fort. Er nahm an, alle Zahlen zwischen 0 und 1 ließen sich auf diese Weise auflisten (hier ohne besondere Ordnung wiedergegeben):

0,1242156743789543...
0,2341176299829547...
0,7763982396546611...
0,4829534479012375...
0,0348109432162984...
..................................
..................................

Cantor betrachtete diese Aufstellung als eine unendliche Liste der unendlich vielen Zahlen zwischen 0 und 1. Doch da machte er eine verblüffende Entdeckung. Er bemerkte, dass er eine Diagonalzahl konstruieren konnte, indem er eine Ziffer von jeder der unendlich vielen Zahlen aus der obigen Liste übernahm. Dazu wählte er die erste Dezimalziffer aus der ersten Zahl der Liste, die zweite aus der zweiten Zahl und so fort ad infinitum. Diese Zahl ist 0,13691...
Jetzt bediente sich Cantor einer sehr klugen Methode. Er veränderte jede Ziffer der Diagonalzahl. Diese Transformation ließ sich beispielsweise dadurch erreichen, dass er zu jeder Ziffer eins addierte, sodass er eine neue Zahl erhielt: 0,24702... Diese neue Zahl ist von allen (unendlich vielen) Zahlen auf der obigen Liste verschieden, weil sie von jeder einzelnen Zahl auf der Liste zumindest in dem Wert der von dieser Zahl übernommenen Ziffer verschieden ist (denn zu dieser Ziffer wurde eins addiert). Da die neue Zahl, die Cantor erzeugt hatte, von allen Zahlen auf der Liste verschieden war, ist es nicht möglich, alle Zahlen zwischen 0 und 1 aufzulisten. Damit war beweisen, dass die Menge aller reellen Zahlen größer ist als die (unendliche) Menge aller ganzen und aller rationalen Zahlen. Wie viel größer die Menge aller reellen Zahlen war als die Menge aller ganzen Zahlen, konnte Cantor allerdings nicht angeben."

 Das ist schon treffend ausgedrückt - und lässt sich doch noch besser veranschaulichen:

erste transzendentale Zahl 0,1242156743789543...
zweite transzendentale Zahl 0,2341176299829547...
dritte transzendentale Zahl 0,7763982396546611...
vierte transzendentale Zahl 0,4829534479012375...
fünfte transzendentale Zahl 0,0348109432162984...
... ...

Dabei müssen in der rechten Spalte natürlich nicht genau die dort vorkommenden Beispiele stehen.

Wichtig - unter der Voraussetzung, dass die transzendentalen Zahlen auch abzählbar sind - ist nur, dass sämtliche transzendentalen Zahlen in einer derartig durchnummerierten Liste anordbar wären.

Nun muss Cantor geahnt haben

(vielleicht weil alle anderen Zahlenmengen - wie oben gezeigt - nur minimale Teile des Zahlenstrahls ausmachten und daher solch ein großer Rest blieb, der Zahlenstrahl aber doch sehr nach kompletter Ausfüllung "roch"),

dass die Voraussetzung "Abzählbarkeit auch der transzendenten Zahlen" falsch war. Er musste also zeigen, dass in der vollständig abgezählten Liste Zahlen fehlten - und da reichte eine einzige solche Zahl.

Und jetzt kommt der (wie immer im Nachhinein simpel aussehende) aberwitzige Geniestreich Cantors - und damit der erste Schritt in höhere, nicht mehr abzählbare Unendlichkeiten - und zwar wieder in einem (sogar vereinfachten, weil nur noch eine einzige Diagonale behandelnden) Diagonalverfahren

(der Mann hatte sozusagen eine "Diagonalenmacke", d.h. er war "schräg gestrickt" und  konnte gar nichts anderes als Diagonalen bzw. sah allüberall nur Diagonalen. Nur: mit dieser höchst einseitigen "Diagonalenmacke" konnte er dennoch "alles" erklären. Es reicht halt im Leben manchmal, in einer einzigen Richtung gut zu sein: man muss sie nur konsequent durchziehen;
bzw. Cantor hatte doch schon bei der Abzählbarkeit so viel Erfolg mit Diagonalen gehabt; da lag es ja wohl nahe, dieses oder ein ähnliches Verfahren auch beim neuen Problem anzuwenden).

Ausgehend von der

(wie sich erst später
herausstellt: falschen)

Annahme, dass die transzendenten Zahlen tatsächlich abzählbar, also in einer solchen Liste wie oben durchnummeriert anordbar seien

(es muss nicht die oben genannte Liste sein, sondern das neue Diagonalverfahren funktioniert für jede solche Liste)

konstruierte er also eine Zahl, die garantiert nicht in der fertigen Liste vorkam.

Zeigen lässt sich das aber eben doch am besten an einem konkreten, also nun mal dem o.g. Beispiel:

Wir betrachten dazu die (ja beliebig weit nach rechts unten fortsetzbare) Diagonale:

   0, 1242156743789543...
   0,2 341176299829547...
   0,77 63982396546611...
   0,482 9534479012375...
   0,0348 109432162984...

Aus diesen markierten Diagonalenziffern lässt sich nun eine erste neue Zahl Z1 bilden, nämlich

Z1 = 0, 13691...

Nun erstellen wir aus der ersten neuen Zahl Z1 eine zweite neue Zahl Z2, indem wir jede Einzelziffer von Z1 verändern

(Hauptsache, da steht nicht mehr dieselbe Ziffer wie vorher),

also z.B. - um eine gewisse Systematik zu haben - um 1 erhöhen:

Am Beispiel also: aus der ersten neuen Zahl

Z1 = 0, 13691...

wird die zweite neue Zahl

Z2 = 0, 24702...

Diese zweite neue Zahl Z2 kann aber in der bestehenden Liste nirgends vorgekommen sein, denn

Weil sich aber nach diesem Schema zu jeder möglichen durchnummerierten Liste transzendentaler Zahlen solche eine nicht in ihr vorkommende transzendentale Zahl Z2 konstruieren lässt, kann es überhaupt keine solche durchnummerierte, vollständige Liste transzendentaler Zahlen geben.

Die (immerhin doch naheliegende) Voraussetzung, dass auch die transzendentalen Zahlen abzählbar wären, hat sich also als falsch erwiesen.

Die transzendentalen Zahlen sind also nicht abzählbar bzw. überabzählbar ("über", weil es ja immer mindestens eine Zahl mehr als auf jeder möglichen Liste gibt).

Zuguterletzt möchte ich weitere Konsequenzen ziehen als Aczel, der für meinen Geschmack allzu früh stehen bleibt, wenn er nur feststellt, dass die transzendenten Zahlen den "Bärenanteil" aller Zahlen auf dem Zahlenstrahl bilden

(wenn er auch anderwärts die religiösen bzw. geradezu metaphysisch-trandzendentalen [!] Implikationen erwähnt, die Cantor mit seinen Untersuchungen verbunden hat, ja das sogar sein Zentralthema ist):

Aczel sagt nach dieser Feststellung nur:

"Alle berühmten irrationalen Zahlen wie Bild und e sind transzendent."

Das Problem dabei scheint mir, dass

Ich zumindest kenne überhaupt nur zwei Beispiele für transzendente Zahlen, nämlich eben Bild und e, während ich unendlich viele

kenne.

Immerhin freut es mich, jetzt zu hören, dass eine besonders einfach konstruierbare (also durchschaubare) irrationale Zahl, nämlich 0, 1 2 3 4 5 6 7 8 9 10 11 12 ..., auch transzendent ist.

Bemerkenswert scheint mir also ein merkwürdiger Widerspruch:

(Nebenbei: die Quadratur des Kreises

[mittels Zirkel und Lineal ein zu einem gegebenen Kreis flächengleiches Quadrat zu konstruieren]

ist auch wieder so ein schönes Mathematikerproblem, dessen "Nährwert" die meisten Laien wohl kaum erkennen können:

  1. Wieso sollte man das überhaupt tun?

  2. Warum diese blödsinnige Beschränkung auf Zirkel und Lineal?
    [Anders geht's nämlich durchaus!]

Zudem zeigt sich hier - wie auch beim Beweis des Satzes von Fermat - wieder ein fatales Problem: der Beweis einer trivial einfachen Aussage [bei der Quadratur wie beim Satz von Fermat, dass ein sehr einfacher Sachverhalt nicht zutrifft] ist teuflisch schwierig und erfolgt vor allem - schon gehirnausrenkend genug - algebraisch. Kein Wunder, dass eine ganze Riege laienhafter Spinner [und oftmals Fanatiker] nach wie vor die Quadratur versucht, obwohl doch [aber eben mit schwierigen, also für viele unzugänglichen mathematischen Mitteln] bewiesen ist, dass sie nicht funktioniert.

Bemerkenswert, ja geradezu typisch für mathematische Sackgassen ist allerdings auch, dass der Nachweis, dass die Quadratur nicht funktioniert, dennoch zu einem - wenn auch nur innermathematisch - "brauchbaren" Ergebnis geführt hat, nämlich der Entdeckung der transzendenten Zahlen.)

Damit scheint mir aber die Mathematik etwas weit über sie hinaus Wichtiges zu belegen, nämlich eine Botschaft, die in vielen Laienaugen vielleicht banal ist, die endlich zu hören gerade vielen MathematikerInneN aber guttun könnte:

es gibt "im Leben" und in der Natur weit mehr als nur das direkt Berechenbare, ja, dieses "weit mehr" macht 99,999 % aus, und Mathematik sowie Naturwissenschaften sind weise Selbstbeschränkungen auf die wenigen Fälle, in denen "das Leben" und die Natur (mit enormem Erfolg!) berechenbar sind.

Nicht umsonst heißen die transzendenten Zahlen "transzendent"

(zwar wählen MathematikerInnen und PhysikerInnen gerne und manchmal auch ironisch "irgendwelche" Namen, die man nun wahrhaft nicht wörtlich nehmen darf: vgl. etwa "Quarks" oder deren "Farben";
aber wenn man grobe Missverständnisse und völlig falsche Anschauungen vermeiden will, wähle man doch lieber Unsinnsnamen wie z.B. "Quarks" [ein Unsinnswort aus dem Roman "Finnegans Wake" von James Joyce, nicht zu verwechseln mit dem deutschen Speisequark]:
der Urheber des Begriffs "transzendente Zahlen" [angeblich James A. Landau 1745 in "Introductio in analysin infinitorum"] wird aber um die "eigentliche" Wortbedeutung gewusst haben, ja ich wette, dass er darauf anspielen wollte, weil ihm diese transzendentalen Zahlen tatsächlich ein wenig "transzendent" anmuteten):

transzendent [lateinisch], die Grenze der Erfahrung überschreitend, übersinnlich, übernatürlich.
(Brockhaus multimedial 2002)

Vgl. auch