Taschenrechner sind uncool
| "In Japan haben wir den Abakus, eine traditionelle Rechenmaschine als Rechenhilfe. | |
| "Es heißt, der Erste Weltkrieg sei der Krieg der Chemiker gewesen, weil zum ersten Mal Senfgas und Chlor eingesetzt wurden, der Zweite Weltkrieg der Krieg der Physiker, weil die Atombombe abgeworfen wurde. Der Dritte Weltkrieg würde der Krieg der Mathematiker werden, weil die Mathematiker die nächste große Kriegswaffe, die Information, kontrollieren würden. Mathematiker haben die [Computer-]Codes entwickelt, die gegenwärtig militärische Informationen schützen. Es überrascht nicht, daß sie auch an vorderster Front im Kampf um die Entschlüsselung dieser Codes stehen." "Sollte es jemals zu einer Kraftprobe zwischen Mensch und Mathematik kommen, so werden die Menschen gut dran tun, die Computer abzustellen." |
Damals im Mathestudium, als ich noch schön und jung war, sagte ein weiser Professor mal, Taschenrechner (die seinerzeit gerade erst auf dem Markt waren) bräuchten wir nicht, denn
rechne ein richtiger Mathematiker eh nie mit konkreten Zahlen (schnöden Einzelfällen), sondern immer mit allen gleichzeitig
("sei n eine [ist doch egal, welche] natürliche/reelle/komplexe Zahl"),
reichten, wenn man dann doch mal Beispielzahlen brauche, um Regeln zu finden, die natürlichen Zahlen von 0 bis 10.
Und in der Tat war mein Taschenrechner nach dem Mathestudium mangels Gebrauch kaputt.
Aus dem Nähkästchen geplaudert:
ein Gespräch schon vor längerer Zeit mit einem Dezernenten
("decernere" = entscheiden, das Sagen haben):
selbstverständlich müsse der Taschenrechner schon in der 5. Klasse
(also nicht, wie an vielen Schulen üblich, in der 7. Klasse)
eingeführt werden - und zwar notfalls auch gegen den Willen der Fachkonferenzen (MathelehrerInnen einer Schule).
Irgendwie noch diskutierbar erschien dem Herrn Dezernenten das nicht.
(Auch ansonsten war er ein liebenswerter Mensch: wenn einE MathematiklehrerIn sich für eine Beförderung bewerbe, aber keinerlei Computerkenntnisse vorweisen könne, habe das drei Folgen:
könne sie/er sich die Beförderung diesmal abschminken,
werde sie/er zu einer Fortbildung in Sachen Computer verdonnert,
komme er, der Dezernent, dann nächstes Jahr noch mal vorbei.
All das sei - wie immer bei Dezernenten! - natürlich keine Einmischung oder - Gott bewahre! - Vorschrift oder Kontrolle, sondern "kollegiale Beratung" :-)
| Ich höre schon die Widerworte: ich argumentiere ja immer nur von der Innermathematik und niemals von Anwendungen aus. In der Tat! |
Weil heute nun mal jeder bei komplizierteren Rechnungen zum Rechner greift, bringt es nichts mehr, gewisse Verfahren beizubringen.
(z.B. die Durchführung komplizierterer Multiplikationen mit der Logarithmentafel [Logarithmus, Numerus], wie sie in meiner Schulzeit noch unvermeidlich war - und die jeder Rechner noch intern anwendet; wer also Computer programmieren will, muss es eben doch wieder können.
Man mache sich die Konsequenzen klar: von allen Logarithmengesetzen braucht man in der Schule nur noch
log (ab) = b • log (a)
denn nur damit kann man Exponentialgleichungen lösen.)
Es bringt nichts mehr, sowas durchzunehmen, weil nur Übung es festigen würde, der Rechner aber gerade diese Übung ersetzt/überflüssig macht.
Zweifelsohne sind auch C[computer]A[lgebra]S[ysteme] ab und zu sinnvoll und hilfreich. Z.B. halte ich es für geradezu sträflich, sie beim Thema "Funktionenscharen" nicht einzusetzen.
Man kann allerdings auch mal fragen: was ist eigentlich, wenn die Rechner mal ausfallen? Und trägt der Rechner nicht doch dazu bei, dass wir
immer weniger wissen, wie (nicht nur mathematische) Dinge funktionieren,
alles einigen Fachwissenschaftler überlassen - mit der Gefahr der Bevormundung und des Missbrauchs?
Damit aber zu den Nachteilen des Rechners.
Computer können zwar mit riesengroßen Zahlen rechnen, aber nicht mit hinter dem Komma unendlichen Zahlen (also periodischen oder irrationalen Zahlen): Rechnerergebnisse sind immer (in der Regel nach der 12. Stelle) gerundet, d.h., dass alle Ziffern, die dann noch kommen, vom Rechner schlichtweg abgeschnitten werden.
Zwar können Taschenrechner neuerdings auch mit Brüchen rechnen. Dennoch seien die entscheidenden Nachteile von Taschenrechnern noch an Brüchen verdeutlicht, weil man da noch leichter zwischen Dezimal- und Bruchschreibweise vergleichen kann.
Während wir z.B. wissen, daß
in Dezimalschreibweise unendlich viele Dreien hinterm Komma hat, also periodisch ist, kennt der Rechner nur 0,333333333333. Alle weiteren Ziffern kann man weder in ihn eingeben, noch kann der Rechner mit ihnen rechnen, noch kann er sie anzeigen. Gegenüber der absolut korrekten Zahl macht der Rechner also immer einen, wenn auch anfangs sehr kleinen Fehler. MathematikerInnen haben es aber nunmal so an sich, absolut genaue Zahlen haben zu wollen, die nichtmal ein Milliardenstel vom exakten Wert abweichen.
Die anfangs kleinen Ungenauigkeiten von Rechnern können zudem auf die Dauer fatale Folgen haben, nämlich von Rechnung zu Rechnung immer größer werden.
Ein Beispiel: angenommen, die exakte Zahl ist 0,333, der Rechner rechnet aber nur mit 0,33. Dann ist der Fehler 0,333 - 0,33 = 0,003, also drei Tausendstel. Weiterhin angenommen, die Ausgangszahl soll mit 2 multipliziert werden. Exakt käme dabei heraus: 2•0,333 = 0,666. Der Rechner hingegen rechnet 2•0,33 = 0,66. Der Fehler ist nun 0,666 - 0,66 = 0,006, er hat sich also bereits auf sechs Tausendstel verdoppelt.
Und so können sich (wie wir insbesondere seit der Chaostheorie wissen) im Laufe mehrerer Rechnungen klitzekleine Fehler zu katastrophal großen Fehlern auswachsen, so dass das Rechnerergebnis hinterher aber auch nicht das mindeste mit dem eigentlichen Ergebnis zu tun hat
(solche anfangs harmlosen und daher unbemerkten, sich aber auf die Dauer fatal vergrößernden Rechenfehler haben schon zu riesigen technischen Katastrophen geführt:
"[...] wie verlässlich sind Taschenrechner und Computer? Liefern sie immer korrekte oder wenigstens fast genaue Resultate? Leider nein, schon ganz einfache Berechnungen können komplett falsche Ergebnisse liefern. Und leider haben auch in der Realität minimale Rechenfehler schon zu fatalen Folgen geführt: Die Ursache für den Absturz der Ariane5-Rakete im Jahr 1996 war z.B. ein simples Berechnungsproblem in der Steuerungs- und Kontrolleinheit der Rakete."
[zitiert nach]
Es ist also nicht nur eine weltfremde Spinnerei von MathematikerInneN, auf möglichst große, am besten sogar absolute Rechengenauigkeit zu achten.)
All diese Überlegungen haben direkte Folgen für den Mathematikunterricht: weil der Rechner so schnell rechnet, neigen viele SchülerInnen dazu, ihn gleich zu Anfang längerer Rechnungen einzusetzen. Der kleine Fehler, den der Rechner dann vielleicht macht, wird aber in jeder weiteren Rechnung schlimmer und wächst sich manchmal zu einem völlig falschen Ergebnis aus. Daraus ist zu folgern:
Rechner sollten - wenn irgend möglich - erst ganz am Ende einer Rechnung eingesetzt werden.
In den meisten Fällen reicht sogar ein Bruch als Ergebnis, und kein Aas will wissen, welcher Dezimalwert dahinter steckt.
Angenommen, nach einer Rechnung kommt als exaktes Ergebnis x =
heraus. Nun ist es ja verständlich, dass man (insbesondere in einer Anwendungs-/Textaufgabe) wissen will, was das ungefähr in Dezimalschreibweise ist. Denn die Dezimalschreibweise ist auf den ersten Blick übersichtlicher. Der Rechner zeigt als Ergebnis von 4:17 folgendes an: 0,2352941. Damit hat er alle Anzeigestellen ausgeschöpft, und wir können uns somit nicht sicher sein, ob bei genauer Rechnung nicht noch weitere Stellen kämen. Eine Rechnung per Hand zeigt sogar, dass tatsächlich noch weitere Stellen kommen. Der Rechnerwert war also zwar ziemlich genau, aber eben nicht absolut genau. Wir dürfen also unter gar keinen Umständen schreiben:
= 0,2352941 (also ein Gleichheitszeichen), sondern höchstens:
≈ 0,2352941 (also ein Ungefährzeichen).
Dieser Genauigkeitsfanatismus der MathematikerInnen hat Folgen bis in Klassenarbeiten hinein. Angenommen, wir haben folgende Aufgabe:
17x = 4
Die korrekte Rechnung wäre:
17x = 4 |: 17
x =
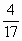
L = {
}
Mit dem Rechner hingegen ergibt sich
17x = 4 |: 17
x ≈ 0,2352941
Erstens fehlt da notwendigerweise das Äquivalenzzeichen (denn aus x ≈ 0,2352941 folgt eben nicht rückwärts auch 17x = 4), und zweitens lässt sich damit nicht mehr die (immer erwartete) Lösungsmenge angeben, denn die Lösungsmenge hat immer absolut exakt zu sein. Wenn überhaupt, so hätten wir erst mittels Bruchrechnung die exakte Lösungsmenge berechnen und erst dann (etwa für eine Anwendung oder um zu zeichnen) den Näherungswert berechnen dürfen. Also:
Rechnereinsatz erst nach Bestimmung der Lösungsmenge!
Sobald von einem Rechenschritt zum anderen gerundet wird bzw. gekappte Dezimalzahlen auftauchen, muss ein Ungefährzeichen auftauchen (vgl. [1]). Rechnet man hingegen mit gerundeten Zahlen oder gekappten Dezimalzahlen exakt weiter, taucht ein Gleichheitszeichen auf (vgl. [2]). Wenn in einer Gleichungskette auch nur ein einziges Ungefährzeichen auftaucht, gilt insgesamt "ungefähr" (vgl. [3]).
Beispiel:
[1] [2]
+
≈0,3 + 0,6 = 0,9
[3]
+
≈ 0,9
Es wird auch schon deutlich, dass es manchmal ganz großer Quatsch ist, mit den Dezimalzahlen des Rechners zu rechnen, ja, dass dadurch alles nur schwieriger wird. Wer z.B.
in den Rechner eingibt und 0,2352941 erhält, muss in allen weiteren Rechnungen diese ellenlange Dezimalzahl eingeben. Und mal angenommen, in einer späteren Rechnung soll
doch wieder mit 17 multipliziert werden: mit Bruchrechenregeln ist das ganz einfach: wenn ich in 4 erst durch 17 teile und später doch wieder mit 17 multipliziere, kann nur glatt 4 rauskommen (und merkwürdigerweise musste ich dazu nie wissen, was
in Dezimalschreibweise ungefähr war). 17 • 0,2352941 zu rechnen, ist hingegen eine ganz schön aufwendige Tipperei und ergibt wegen der rechnerinternen Rundung oftmals nicht genau 4.
Auch wenn's mir keiner glaubt: Bruchrechnung vereinfacht vieles ungeheuer. Denn natürlich ist
•3 wieder glatt 1, während die Rechnung 3 • 0,3 (Periode 3) nicht nur besonders kompliziert, sondern schlichtweg unmöglich ist. Denn schauen wir uns mal an, was
3 • 0,3 denn eigentlich bedeutet: 3 • 0,3 = 0,3 + 0,3 + 0,3 bzw.
0,3333333333333333333333...
+ 0,3333333333333333333333...
+ 0,3333333333333333333333...
Nun wissen wir aber von der Addition "mit der Hand", dass man solche Additionen mit der letzten Stelle anfängt. Da jede der drei zu addierenden Zahlen aber unendlich viele Stellen hinterm Komma hat, gibt es keine solche letzte Stelle hinterm Komma.
Wenn wir deshalb aber mal notgedrungen (und regelwidrig!) mit der ersten Stelle (oder auch der letzten auftauchenden) anfangen, so ergibt sich:
0,3333333333333333333333...
+ 0,3333333333333333333333...
+ 0,3333333333333333333333...
= 0,9999999999999999999999...,
also 0,9. Das aber ist zwar nicht falsch
(denn ohne Erklärung: 0,9 ist aus komplizierteren mathematischen Gründen dasselbe wie 1),
aber dennoch irritierend, da wir ja das glatte Ergebnis 1 erwarten.
Spätestens mit irrationalen Dezimalzahlen kann man überhaupt nicht (genau) rechnen, mit der Wurzelschreibweise aber wunderbar!!!
Kommt hinzu: eineN richtigeN MathematikerIn interessiert doch nicht die Bohne der Dezimalwert/die Größenordnung von
, sondern einzig und allein, dass
•
exakt gleich 2 ist.
MathematikerInnen jonglieren also wunderbar mit Schachteln, ohne zu wissen (wissen zu müssen), was in ihnen drin ist.
Der Taschenrechner hat den entscheidenden Nachteil, dass SchülerInnen bestimmte Zahlenarten und Rechenverfahren für sie überhaupt nicht mehr lernen:
Brüche und Bruchrechnung,
irrationale Zahlen und der Umgang mit ihnen,
Potenzen und Potenzgesetze,
Fakultäten.
Genau gesagt: es gibt - mit Tachenrechner - überhaupt keinen ersichtlichen Grund, beispielsweise Potenzen und Fakultäten als sinnvolle Abkürzungen kennen zu lernen.
Nehmen wir nur beispielsweise die Potenzen: wer einen Taschenrechner benutzt, braucht sie (und ihre Regeln) eigentlich gar nicht mehr, da sich genauso gut mit dem Ergebnis 1024 wie mit 210 rechnen lässt.
(Potenzen als Schreibweise für immens große [oder kleine] Zahlen, also z.B.
9999999999999 • 9999999999999 ≈
kommen ja kaum im Mathematikunterricht, sondern "nur" in Physik und Chemie vor:
- Avogadrosche Zahl NA ≈ 6,022·1023
Anzahl der Atome im Universum etwa in der Größenordnung 1078)
Wie praktisch Potenzen als Abkürzungen von Multiplikationen und diese wiederum als Abkürzungen von Additionen sind
(und dass demnach Potenzen rasante Abkürzungen für Additionen, aber auch dementsprechend abstrakt sind),
wird SchülerInneN also gar nicht mehr klar.
Viel schlimmer aber: wer immer sofort (durch den Taschenrechner allzu einfach) ausrechnet, erkennt nie Systematisches, sondern taumelt nur von Zahl zu Zahl (vgl. ![]() ).
).
Aus all dem folgt
(und man bedenke, dass Beweise der eigentliche Kern der Mathematik sind):
Vor allem können Rechner/Computer bisher eins nicht: irgendwas beweisen (außer dem ![]() Beweis des Vierfarbtheorems?). Wenn man also in einer Zeitung liest "Ein Großcomputer hat jüngst bewiesen, dass ...", so ist das schlichtweg Quatsch: ein Computer kann sicherlich in kurzer Zeit massenhaft Fälle durchrechnen, aber nicht - wie Mathematiker mit einigen Tricks - ausnahmslos alle. Computerergebnisse können Vermutungen also aufgrund der Fülle der durchrechneten Fälle nur wahrscheinlicher erscheinen lassen.
Beweis des Vierfarbtheorems?). Wenn man also in einer Zeitung liest "Ein Großcomputer hat jüngst bewiesen, dass ...", so ist das schlichtweg Quatsch: ein Computer kann sicherlich in kurzer Zeit massenhaft Fälle durchrechnen, aber nicht - wie Mathematiker mit einigen Tricks - ausnahmslos alle. Computerergebnisse können Vermutungen also aufgrund der Fülle der durchrechneten Fälle nur wahrscheinlicher erscheinen lassen.
| Es gibt also Phasen im Unterricht, in denen man den Taschrechner zumindest zeitweise verbieten sollte. Und ich persönlich würde dazu neigen, ihn überhaupt erst einzuführen, nachdem die Wurzeln gefestigt sind, also gegen Ende der neunten (!) Klasse. |
| PS: | "Der Extremwert liegt (ungefähr) bei 1,4142" ist in Mathematikerohren natürlich eine potthässliche Antwort. Mit herablassendem Ton: sowas überlassen wir Physikern. Eine bildschöne Antwort ist hingegen: "Der Extremwert liegt (exakt) bei (Sowieso kann ich mir ganze Oberstufenklausuren vorstellen, in denen man nun wahrhaft keinen Taschenrechner mehr braucht.)
|  |
| PPS: | Was ist eigentlich, wenn die Computer/Taschenrechner aus irgendeinem Grunde ausfallen?
Wir bräuchten dann doch dringend wieder - mathematisch gesehen -
| |