

Was, zum Teufel, soll
(wie derzeit weltweit modern)
penetrant bunt-bewegten Intro

 die
ach so bedeutsame "breaking news" sein?!
die
ach so bedeutsame "breaking news" sein?!  sieht doch so aus, als wenn ein minimalistischer moderner „Künstler“
sieht doch so aus, als wenn ein minimalistischer moderner „Künstler“
(vgl. das erzreaktionäre Buch
 )
)
rein zufällig, also ohne Sinn & Verstand
(und sowieso ohne alles handwerkliche „Können“)
massenhaft schwarze Tropfen auf eine Leinwand hat tröpfeln lassen
(vgl.
)
und das Ergebnis großspurig zur „Kunst“ erklärt hat
(die die Schickeria dann sicherlich auch brav für teures Geld als Statussymbol oder Anlageobjekt kauft;
nebenbei: mein Kunstlehrer hat mal gesagt: "Kunst ist, wo kein Hubschrauber mehr landen kann", und überhaupt reicht es oft, ein möglichst großes Bild in einem ordentlichen Rahmen an die Wand zu nageln, und schon macht es Eindruck:
 ).
).
Wie es sich für richtige „Kunst“ gehört, kann man in
 auch so
ziemlich alles rein(!)interpretieren:
auch so
ziemlich alles rein(!)interpretieren:
Oder
„Der Künstler dekonstruiert mit seiner Punktwolke mutig das kausale Denken und damit die den Menschen versklavende kapitalistische Logik.“
Mit der „Tröpfeltechnik“ ähnelt das Bild
 Werken
des
Werken
des
![]() „Pointillismus“, die aus massenhaft einzelnen Punkten zusammengesetzt sind wie
z.B. in
„Pointillismus“, die aus massenhaft einzelnen Punkten zusammengesetzt sind wie
z.B. in  .
.
Aber dieses scheinbar rein zufällig hingekleckste Bild ist nur ein Ausschnitt aus dem Bild
(George Seurat: Tour Eiffel).
Bei "hinreichend großer Datenmenge" (s.o.), nämlich dem ganzen Bild, wird der Ausschnitt also als konkretes Detail des Eiffelturms, nämlich als dessen Spitze, erkennbar.
Was an  auffällig ist, wird deutlich(er), wenn man es mit dem tatsächlich rein zufällig
erstellten Bild
auffällig ist, wird deutlich(er), wenn man es mit dem tatsächlich rein zufällig
erstellten Bild  vergleicht.
vergleicht.
Um diesen Vergleich zu vereinfachen, hier nun beide Bilder direkt nebeneinander:


Ich hoffe, dass spätestens hier klar wird:
in Bild 2 wirken die Punkte tatsächlich zufällig verteilt, d.h.
es sind zwar einzelne mehr oder weniger regelmäßige
Teilstrukturen wie z.B.
![]() (vergrößert
(vergrößert
![]() ) erkennbar,
) erkennbar,
aber keine wiederkehrenden Muster;
in Bild 1 hingegen deuten sich regelmäßige Muster an, nämlich diagonale Strecken:

Könnte es sein, dass wir senkrechte und waagerechte Strecken leichter erkennen?:
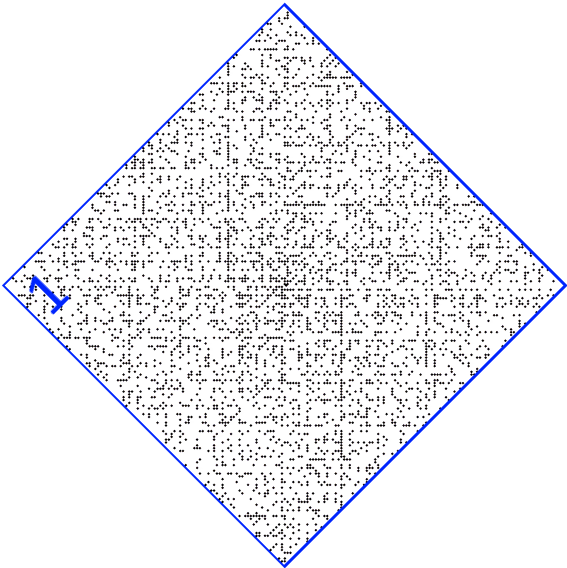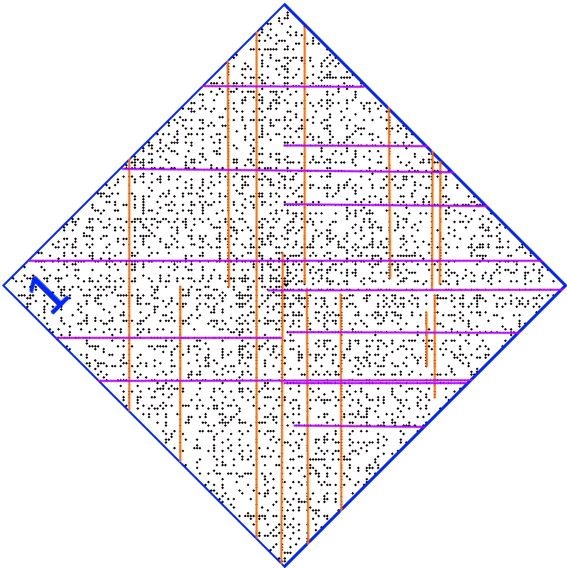

Angenommen mal, Bild 1 wäre von einem Künstler geschaffen worden. Dann läge der Verdacht nahe, dass er
die Punkte nicht rein zufällig auf die Leinwand getröpfelt,
sondern ab und zu absichtlich regelmäßige Strukturen (Strecken) angedeutet hätte.
„angedeutet“, weil die Strecken nie durchgehend, sondern immer wieder unregelmäßig durchbrochen sind.
Aber all das ist nur ein Verdacht, da natürlich auch Regelmäßigkeiten wie z.B.

rein zufällig entstehen können
(und zwar mit derselben Wahrscheinlichkeit wie jede andere [zufällig aussehende] Punkteanordnung).
„Wer am Ende ist, kann von vorn anfangen,
denn das Ende ist der
Anfang von der anderen Seite.“
(Karl Valentin)
Wenn
 ab und zu regelmäßige Muster (Strecken) enthält, ist das ja schön (?) und gut,
wird dadurch allerdings noch lange nicht der Titel
ab und zu regelmäßige Muster (Strecken) enthält, ist das ja schön (?) und gut,
wird dadurch allerdings noch lange nicht der Titel
 verständlich.
verständlich.
Um das zu klären, müssen wir ganz an den Anfang zurückspringen
(und später nach einem ellenlangen Umweg zum Ende, also
 , zurückkehren):
, zurückkehren):
: das mathematische Teilgebiet der "Zahlentheorie"

![]()
Wohl gerade wegen dieser "Schizophrenie" hat
![]() Carl Friedrich Gauß, „der Fürst der Mathematik“, gesagt:
Carl Friedrich Gauß, „der Fürst der Mathematik“, gesagt:

(… und die Primzahlen sind die Königinnen
 der Zahlentheorie!)
der Zahlentheorie!)
gibt es eine Hierarchie
 der natürlichen
Zahlen
der natürlichen
Zahlen
(wobei der Vergleich allerdings hinkt: nicht die zusammengesetzten Zahlen „tragen“ die Primzahlen, sondern umgekehrt):
1 + 1 = 2 ; 2 + 1 = 3; 3 + 1 = 4 … 1000 + 1 = 1001 …
![]()
![]()
Z.B. 6 = 2 • 3 und 18 = 2 • 3 • 3 .
Man könnte also sagen:
 ,
,
 (hier Wasser), die aus den
Elementen ( Primzahlen )
zusammengesetzt sind.
(hier Wasser), die aus den
Elementen ( Primzahlen )
zusammengesetzt sind.
Die Tatsache, dass alle (!) Nicht-Primzahlen aus Primzahlen zusammengesetzt werden können, nennt man den (bewiesenen!)
„Fundament alsatz der Arithmetik“,
alsatz der Arithmetik“,
womit seine enorme Bedeutung für die Zahlentheorie deutlich wird.
(Zu diesem Beweis siehe ![]() Der Beweis gehört unbedingt in Schulen, gerade weil er so aberwitzig
ist!)
Der Beweis gehört unbedingt in Schulen, gerade weil er so aberwitzig
ist!)
: selbstverständlich suchen die Mathematiker nach einer Regel, nach der die Primzahlen verteilt sind. Ideal wäre da eine (einzige und zudem möglichst einfache) Formel, mit der man jede der unendlich vielen Primzahlen berechnen könnte.
Wenn man dann z.B.
Schauen wir uns also mal an, wie die Primzahlen in den natürlichen Zahlen verteilt sind. Wir beginnen dazu der Einfachheit halber mit den ersten acht natürlichen Zahlen:
![]()
Nun
wird die 1 von Mathematikern sowieso nicht als Primzahl angesehen
und ist die 2 eine ganz besondere Primzahl:
sie ist in der Tat eine Primzahl, weil sie nur durch 1 und sich selbst (also 2 ) teilbar ist
(kleinere Primzahlen als 2 , aus denen sie zusammengesetzt sein könnte, gibt es ja auch gar nicht);
(dann wären sie ja doch Primzahlen),
Alle weiteren geraden Zahlen (4, 6, 8 …) sind also zusammengesetzte Zahlen:
![]()
Es folgt:
(nämlich alle geraden Zahlen außer der 2)
sind zusammengesetzte und somit keine Primzahlen,
(wieder außer der 2)
nur ungerade Zahlen können
(müssen aber nicht)
Primzahlen sein.
Wenn wir nun aber in der Liste
![]() die 1 und die
2 mal weglassen, bleiben
die 1 und die
2 mal weglassen, bleiben
![]() .
.
Wegen dieses einfachen Musters vermuten wir die einfache Regel:
Primzahlen und zusammengesetzte Zahlen wechseln sich in alle Ewigkeit ab …
Nach dieser Regel müsste die nächste Zahl, also die 9 , eine Primzahl sein - ist sie aber nicht, denn 9 = 3 • 3.
… womit die ganze gerade erst vermutete Regel an einem einzigen Beispiel (der 9 ) gescheitert und damit endgültig falsch ist.
Und noch eines können wir folgern:
Anders gesagt: Primzahlen (außer der 2 und der 3) können nie direkt nebeneinander liegen.
Primzahlen aber, zwischen denen
eine einzige (gerade) zusammengesetzte
Zahl liegt, nennt man "Primzahlzwillinge"
 (s.u.).
(s.u.).
Beispiele für solche Primzahlzwillinge sind in
![]()
Und für die ersten hundert natürlichen Zahlen:

Auf der Suche nach einer möglicherweise vielleicht vorhandenen Regel für das Auftreten von Primzahlen schauen wir uns nun mehr natürliche Zahlen an, nämlich z.B. die ersten hundert.
Schon bei diesen nur hundert Zahlen ergibt sich allerdings ein Problem, das unten noch wegweisend werden wird:
es gelingt uns nämlich nicht, sie übersichtlich
(z.B. auf einem DIN-A4-Papier im Querformat)
nebeneinander aufzuschreiben:
entweder reicht der Platz nicht für alle 100 Zahlen:

oder die Zahlen sind unleserlich klein:
 ,
,
oder wir schreiben die hundert natürlichen Zahlen auf einen langen Papierstreifen. Allerdings können wir da
immer nur einen sich bewegenden Ausschnitt
| , |
Kleines Zwischenspiel:
kein Mensch ist in der Lage, in dem langen Streifen
irgendeine Ordnung zu entdecken, aber alles wird ganz einfach, wenn wir den Streifen zerschneiden und die Schnipsel untereinander (zweidimensional) anordnen:

Da ist dann plötzlich
(wenn auch arg pixelig)
der amerikanische Präsident Abraham Lincoln
 erkennbar.
erkennbar.
Schreiben wir also die ersten hundert natürlichen Zahlen jetzt mal in mehreren gleichlangen Zeilen untereinander bzw.
(umständlich gesagt)
in der „ersten Schlangenform“

auf:
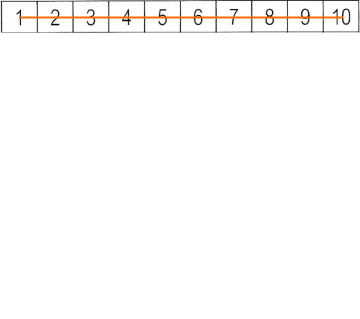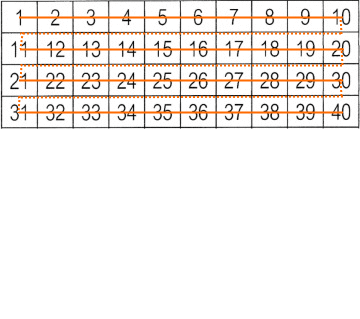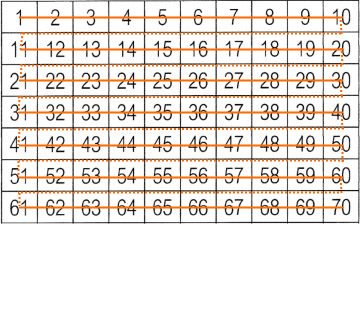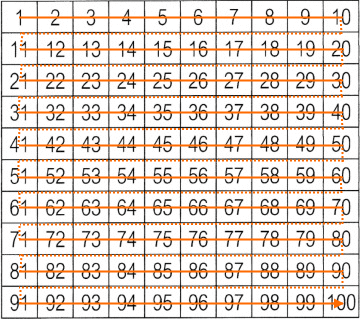
Oder kurz:
(… was nun endlich gut lesbar auf eine DIN-A4-Seite passt
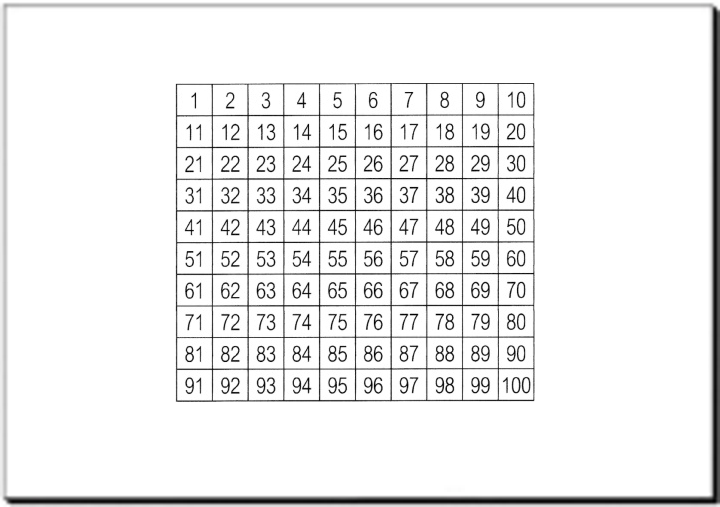 ,
,
weil wir jetzt die beiden Dimensionen [Breite
und Höhe] der Seite ausnutzen.
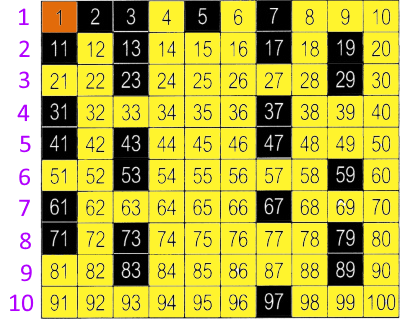
Wenn wir jetzt noch die Primzahlen und die zusammengesetzten Zahlen markieren, erhalten wir
 .
.Die Frage nach einer Regel dafür, wie die Primzahlen in den natürlichen Zahlen verteilt sind, läuft hier erstmal darauf hinaus, unabhängig von den einzelnen Zahlen ein optisches Muster zu erkennen:

Insbesondere fällt da die dritte Spalte von links auf, also
![]() :
:
zwar stehen da leider nicht
(was für eine Regel doch sehr schön wäre)
ausschließlich Primzahlen,
aber immerhin doch überdurchschnittlich viele, nämlich sieben von zehn, und drei davon sogar direkt untereinander, nämlich
(jetzt wieder mit Zahlen)
![]() .
.
In der Tat sind 3 , 13 und 23 allesamt Primzahlen, aber warum stehen sie übereinander?: weil
 vorgenommen haben
vorgenommen haben(alle Zahlen mit derselben Endziffer [also z.B. auch 4, 14 und 24 ] stehen untereinander).
Wir hätten aber genauso gut z.B. nach dem Zwölfersystem
 vorgehen, also nach jeweils
zwölf Zahlen einen Zeilensprung machen können
vorgehen, also nach jeweils
zwölf Zahlen einen Zeilensprung machen können
 ,
,
und schon
(die aber im Zehnersystem nicht untereinander stehen).
Die zweidimensionale Anordnung in gleichlangen Zeilen ist also nicht geeignet, eine Regel für das Auftreten von Primzahlen zu finden.
Kurz zurück zu  : wir
hatten da den Streifen
: wir
hatten da den Streifen
in 12er-Schnipsel zerschnitten und diese untereinander gelegt.
Wenn wir den Streifen aber in 10er-Schnipsel
zerschneiden und diese untereinander legen, ergibt sich 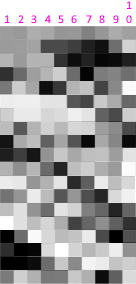 , und da
ist kein Lincoln mehr erkennbar.
, und da
ist kein Lincoln mehr erkennbar.
Jetzt sei es endlich verraten: die Mathematiker haben
in den letzten 2000 Jahren
anhand der Primzahlen viel über die natürlichen Zahlen
und auch viel über Primzahlen herausgefunden
(vgl. das phantastische populärwissenschaftliche Buch
 ),
),
aber trotz unendlicher Bemühungen noch keine Formel gefunden, mit der man jede der unendlich vielen Primzahlen berechnen könnte.
Könnte es also sein,
(nur
 sie kennt?),
sie kennt?),
(die Mathematiker also einfach zu dumm sind),
 Kurt Gödel als möglich gezeigten Vermutungen ist, die
Kurt Gödel als möglich gezeigten Vermutungen ist, die
(wie die Existenz des lieben Gottes)
niemals bewiesen, aber auch nicht widerlegt werden können, also grundsätzlich unentscheidbar sind.
(Schlimmer noch: solange nicht ein
Beweis oder eine
Widerlegung vorliegt, werden wir nicht erfahren, ob solch eine Vermutung unentscheidbar ist und somit alle Beweis- oder Widerlegungsversuche verlorene
Liebesmüh‘ sind. Vgl.  .)
.)
Es ist aber noch ein zweiter Grund dafür denkbar, dass nicht entschieden werden kann, ob die Primzahlen innerhalb der natürlichen Zahlen zufällig : echter Zufall lässt sich niemals beweisen, denn um ihn zu beweisen, müsste man den Zufall paradoxerweise mit einer Regel erfassen.
Wenn also die Primzahlen tatsächlich zufällig verteilt sein sollten, werden wir das nie erfahren - und werden Mathematiker wohl ewig versuchen, eine Regel zu finden. Erst wenn sie diese gefunden hätten, wäre der Zufall ausgeschlossen.
Schon seit Langem haben sich die Mathematiker
Ein erstes Beispiel:

Kürzer:

Noch kürzer:
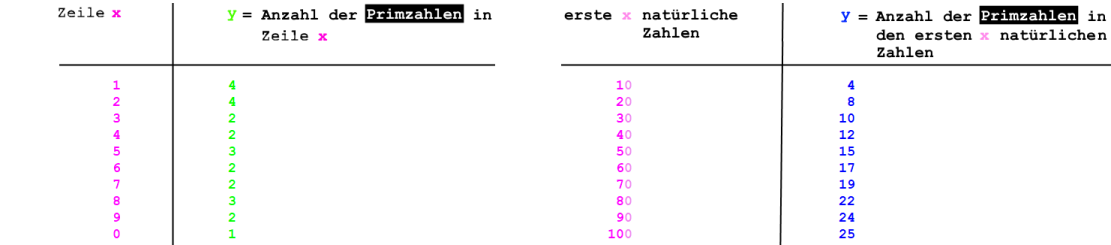
In
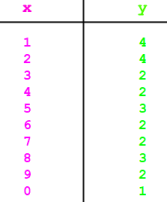 ist nur schwerlich ein Trend zu
entdecken:
ist nur schwerlich ein Trend zu
entdecken:
Wo der Trend aber so schwach ist: wieso sollte man da überhaupt noch weiterdenken und in sehr große Zahlen ausgreifen?
Zweites Beispiel:
wir schauen uns die ersten Millionen natürlichen Zahlen an,
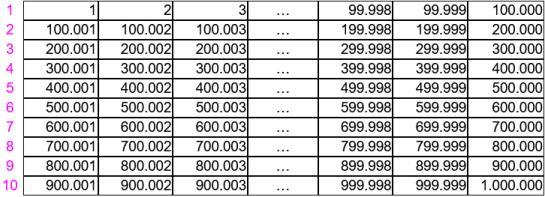
Hier wird's schön abstrakt:
wir können die Zeilen nicht aufschreiben, da wir nicht jeweils hunderttausend Zahlen nebeneinander auf ein Blatt Papier bekommen würden, und hunderttausend Zahlen lange Streifen wären sowieso sehr unübersichtlich;
außerdem sind wir viel zu faul, Millionen Zahlen aufzuschreiben;
Aber für das, was wir im Folgenden vorhaben, müssen wir
Damit ergibt sich
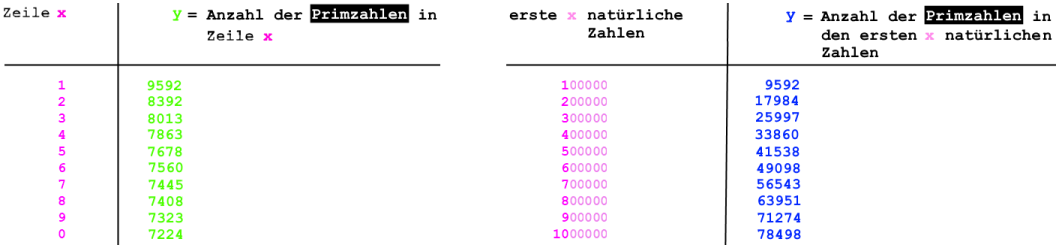
In
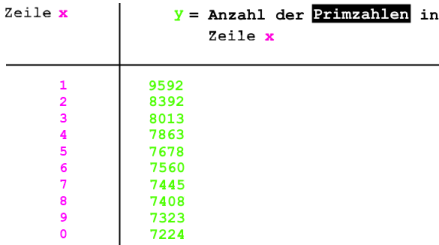 hat
sich der oben noch schwache Trend durchgesetzt, dass in den aufeinander
folgenden Zeilen immer weniger Primzahlen vorkommen.
hat
sich der oben noch schwache Trend durchgesetzt, dass in den aufeinander
folgenden Zeilen immer weniger Primzahlen vorkommen.
(Es bleibt allerdings zumindest vorerst ein Trend, denn wir wissen nicht, ob es für mehr als eine Millionen Zahlen nicht doch wieder Ausnahmen gibt.)
Halten wir also mal die Vermutung fest:
je größer die Anzahl der natürlichen Zahlen, desto weniger Primzahlen kommen “im Schnitt“ hinzu.
Das aber heißt auch:
je größer die Anzahl der natürlichen Zahlen, desto weiter liegen die Primzahlen “im Schnitt“ auseinander.
Die Einfügung "im Schnitt" ist nötig, weil eventuell wieder "nur" ein Trend mit Ausnahmen vorliegt, denn es scheint trotz des Trends immer wieder (unendlich viele) Primzahlzwillinge (s.o.) zu geben, die sehr nah beieinander liegen.
Mit "scheint" haben wir uns aber schon wieder die nächste Unwägbarkeit eingehandelt:
"Obwohl unendlich viele Primzahlen existieren, ist es ungewiss, ob es unendlich
viele Primzahlzwillinge gibt. Die Primzahlzwillings-Vermutung besagt, dass es
unendlich viele Primzahlzwillinge gibt. Sie ist eine der großen offenen Fragen
der Zahlentheorie."
(Quelle:
![]() )
)
Zwischendurch mal eine Veranschaulichung dafür, dass ein durchgehender Trend bestehen kann, auch wenn es immer wieder Ausnahmen gibt:
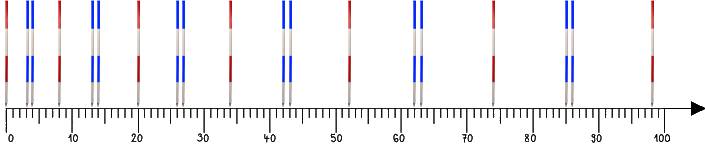 :
:
die Stäbe liegen offensichtlich von links nach rechts "im Schnitt" immer weiter auseinander,
obwohl zwischendurch immer wieder zwei blaue Stäbe (Primzahlzwillinge) nah beieinander liegen.
Nach all den windelweichen Formulierungen, nämlich
unbewiesenen Vermutungen,
„Trends“ (mit Ausnahmen)
und „im Schnitt“,
nun aber endlich mal
 „richtige“
Mathematik, nämlich etwas Bewiesenes
„richtige“
Mathematik, nämlich etwas Bewiesenes
(und damit ein Highlight der Zahlentheorie, wenn nicht gar der gesamten Mathematikgeschichte).
Schauen wir uns dazu nochmals die Verteilung der Primzahlen unter den ersten hundert natürlichen Zahlen an:

Jetzt soll es im Gegensatz zu oben allerdings um die rechte Tabelle gehen, also um
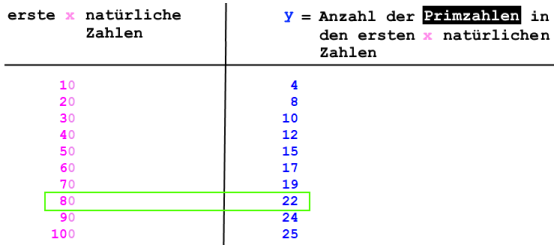 .
.
Wenn man diese Zahlen in ein Koordinatensystem einträgt, erhält man
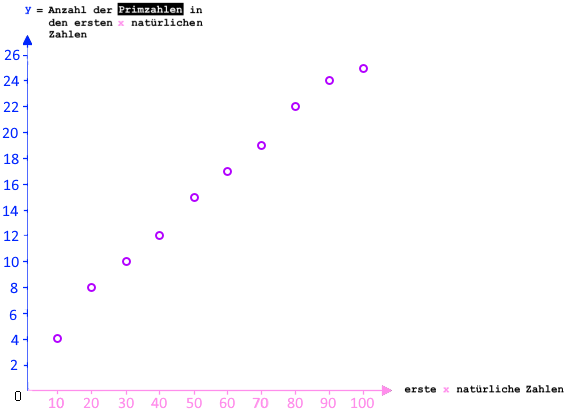
(die y-Achse hat einen größeren Maßstab als die x-Achse, d.h. der Graph ist nach oben gestreckt).
Am Beispiel
![]() :
:
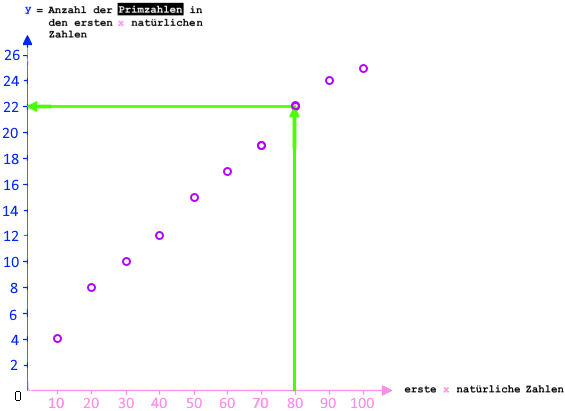
Unter den ersten 80 natürlichen Zahlen (1, 2, 3 ... 78, 79, 80) sind also 22 Primzahlen.
Schauen wir uns
nun
 genauer an:
genauer an:
da immer neue Primzahlen hinzukommen, liegt jeder neue Punkt Ο (weiter rechts) höher als die alten Punkte;
die Punkte liegen also auf einer ansteigenden Linie:
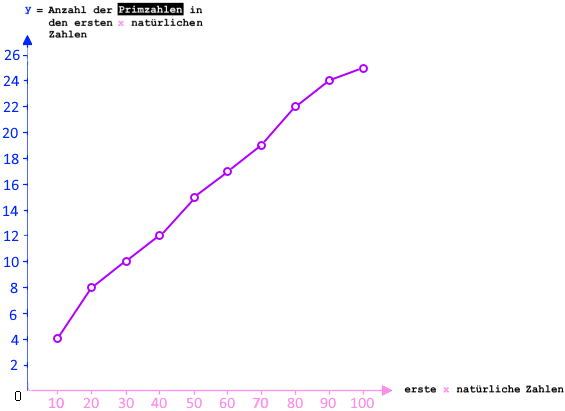 ;
;
diese Linie ist aber nicht hübsch geschwungen, sondern
"eckig": 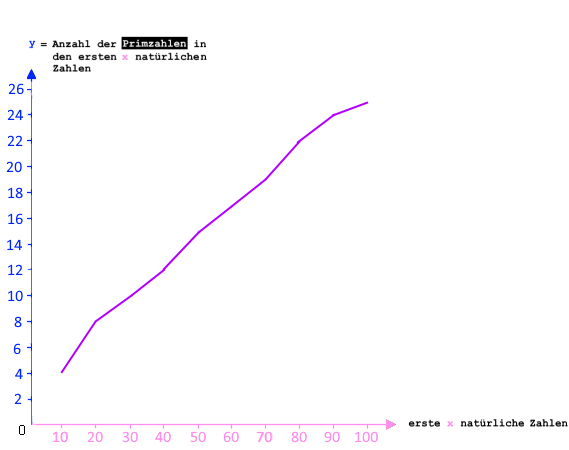 ;
;
wenn Mathematiker sowas
 sehen,
denken sie sofort an einen Funktionsgraphen, der aber gerade oder hübsch
geschwungen sein sollte;
sehen,
denken sie sofort an einen Funktionsgraphen, der aber gerade oder hübsch
geschwungen sein sollte;
also versuchen sie es mit einer
Näherung ("Abschätzung"; s.u.), die z.B. so aussehen könnte:
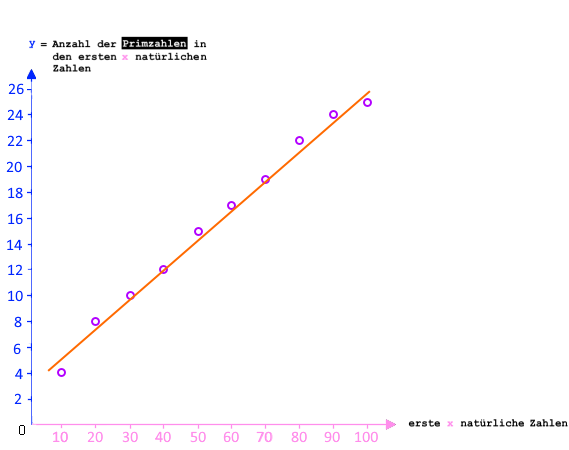 .
.
Es wundert einen schon gar nicht mehr, dass es der große Carl
Friedrich Gauß höchstpersönlich war, der 1793 die Vermutung aufgestellt hat,
dass die Funktion mit der Funktionsgleichung
![]() eine gute
Näherung ist
eine gute
Näherung ist
(auch wenn das für die ersten hundert natürlichen Zahlen noch nicht so aussieht):
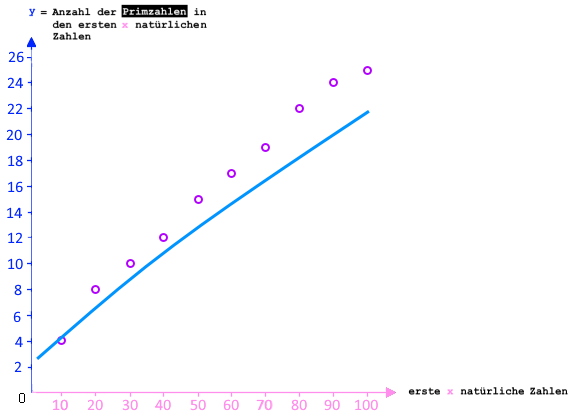
Für Laien ist die Funktionsgleichung
![]() sicherlich ein
Buch mit sieben Siegeln, und zwar insbesondere, weil da im Nenner ein “natürlicher Logarithmus“ vorkommt.
sicherlich ein
Buch mit sieben Siegeln, und zwar insbesondere, weil da im Nenner ein “natürlicher Logarithmus“ vorkommt.
(Aber Schüler ab der 10. Klasse sollten den Logarithmus kennen, wobei insbesondere der „natürliche“ Logarithmus für sie allerdings meistens arg „unnatürlich“ bleibt,
[alle Klarheiten beseitigt?]
Dennoch ist
![]()
(z.B. im Vergleich mit
![]() )
)
relativ einfach, nämlich
ein simpler Bruch
mit dem simplen Zähler x
und dem zugegebenermaßen nicht mehr ganz so simplen Nenner ln(x).
Aber man muss an der Formel
![]() ja gar nicht
alles verstehen - außer einer Eigenschaft:
ja gar nicht
alles verstehen - außer einer Eigenschaft:
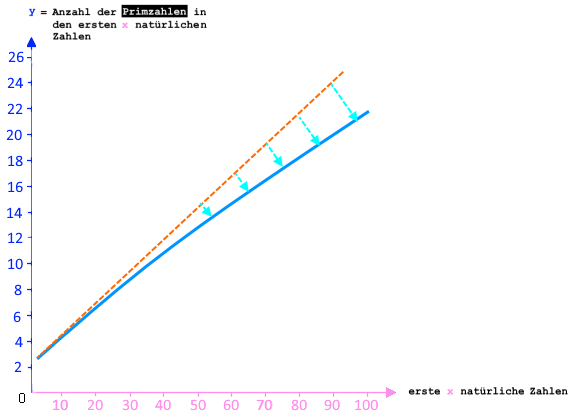
Der Funktionsgraph
steigt zwar in alle Ewigkeit,
wird aber trotzdem immer flacher, d.h. er ist eine Rechtskurve, was eben bedeutet: es kommen immer weniger Primzahlen hinzu.
Erstes Beispiel für
![]() :
:
wir betrachten die ersten hundert natürlichen Zahlen (s.o.):
 ;
;
![]() bedeutet dabei, dass in den ersten 80 natürlichen Zahlen 22
Primzahlen vorkommen;
bedeutet dabei, dass in den ersten 80 natürlichen Zahlen 22
Primzahlen vorkommen;
mit
![]() ergibt sich
hingegen
ergibt sich
hingegen ![]() bzw. kurz
bzw. kurz ![]() ;
;
es ergibt sich also ein ziemlich großer Fehler von
![]() ≈ 18 % .
≈ 18 % .
Zweites Beispiel: wir betrachten die ersten Millionen natürlichen Zahlen (s.o.):
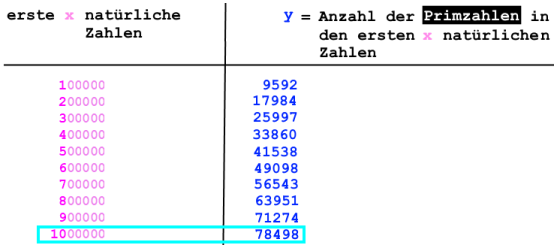 ;
;
Wenn überhaupt, so nähert sich
![]() also für sehr
große x nur quälend langsam der Anzahl der Primzahlen bis
x.
also für sehr
große x nur quälend langsam der Anzahl der Primzahlen bis
x.
(Inzwischen gibt es
eine sehr viel bessere, weil schnellere und doch sehr ähnliche Annäherung als ![]() , nämlich
, nämlich 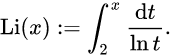 Vgl.
Vgl.
![]() .)
.)
Es ist mir ein Rätsel, wie Gauß auf die Gleichung
![]() gekommen ist.
gekommen ist.
Aber selbst ihm ist es nicht gelungen, seine Vermutung zu
beweisen. Sondern dieser Beweis konnte erst hundert Jahre später durch Jacques
Salomon Hadamard und Charles-Jean de La Vallée Poussin erbracht werden (vgl.
![]() ).
).
(Die verschiedenen Beweise sind derart kompliziert, dass sie in der Schule wohl kaum behandelt werden können - und also auch hier nicht auftauchen):
Es ist also seitdem bewiesen und somit keine Vermutung mehr, sondern ein mathematischer "Satz":
![]() nähert sich für sehr große x immer mehr der Anzahl der Primzahlen bis zur Zahl
x
an.
nähert sich für sehr große x immer mehr der Anzahl der Primzahlen bis zur Zahl
x
an.
(Im selben Augenblick, in dem eine Vermutung bewiesen ist, ist sie schon keine Vermutung mehr, sondern ein „Satz“:
Vgl. den „Satz des Pythagoras“: Pythagoras hat angeblich als Erster bewiesen, was bis dahin nur eine Vermutung war.)
Wenn wir nun die Anzahl der Primzahlen bis zur natürlichen
Zahl x kurz als ![]() bezeichnen
bezeichnen
(wobei mit dem Buchstaben
![]() hier
also ausnahmsweise mal nicht die Kreiszahl
hier
also ausnahmsweise mal nicht die Kreiszahl
![]() ≈
3,14159265358979 gemeint ist),
≈
3,14159265358979 gemeint ist),
so lautet der "Satz"
![]() nähert sich für sehr große
x
immer mehr
nähert sich für sehr große
x
immer mehr
![]() an:
an:
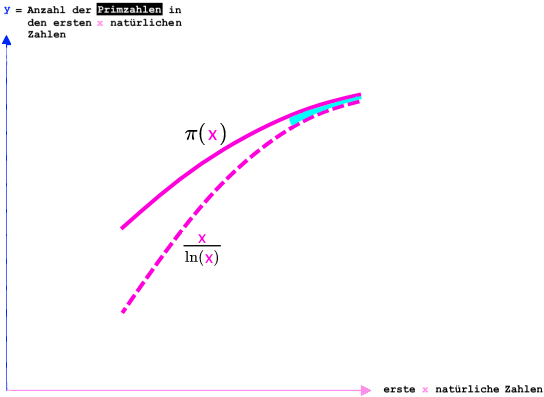
![]() schmiegt sich also für sehr große
x immer mehr an
schmiegt sich also für sehr große
x immer mehr an
![]() an.
an.

In mathematischer Schreibweise:
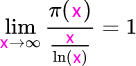
Solch einer abstrakten Gleichung muss man aber eine Bedeutung geben
(die ein "richtiger" Mathematiker natürlich sofort erkennt):
für sehr große x nähert sich der Bruch
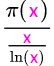 immer mehr
der 1 an;
immer mehr
der 1 an;
woraus folgt:
die Zahlen
![]() und
und
![]() werden
annähernd gleich groß,
werden
annähernd gleich groß,
also
![]() ≈
≈
![]() ,
,
d.h. die Funktion
![]() kommt
kommt
![]() unendlich nah.
unendlich nah.
(Ich ahne schon, dass "richtigen" Mathematikern bei solch laxer umgangssprachlicher Umschreibung des Limes schlecht wird. Aber ich versuche in diesem Essay ja nur so zu sprechen, dass sogar Laien oder Schüler ab der 8. [!] Klasse es verstehen können.)
Wir hatten schon gesehen, dass diese Annäherung quälend langsam ist
(bei x = 1.000.000 ist der Fehler noch immer ca. 11 %).
Aber für gigantisch große x geht der Fehler eben doch gegen 0.
Und Mathematikern ist es sowieso erstmal herzhaft egal, ob die Annäherung langsam oder schnell voran geht, Hauptsache, „am Ende“ findet sie hautnah statt.
Auch der mathematische Satz
![]() nähert sich für sehr große x
immer mehr
nähert sich für sehr große x
immer mehr
![]() an
an
bedarf wieder einer (doppelten) Deutung:
ist es doch schon erstaunlich, dass
die Anzahl der Primzahlen unter den ersten x natürlichen Zahlen,
obwohl man gar nicht weiß, wo diese (unendlich vielen!) Primzahlen liegen!
(Das ist etwa so, als wenn wir
 .
.Und genau solch eine aberwitzige Denkweise ist "typisch Mathematik".)
zeigt der Satz aber vor allem,
|
dass die Primzahlen
|
Da liegt doch die Frage nahe, ob es noch weitere solche
Regeln für das Auftauchen von Primzahlen gibt, und zwar am liebsten
solche, die
|
Nebenbei: der mathematische „Satz“
![]() nähert sich für sehr große x
immer mehr
nähert sich für sehr große x
immer mehr
![]() an
an
ist neben Euklids „Satz“, dass es unendlich viele Primzahlen gibt, der wohl wichtigste Primzahlsatz und wird deswegen
nicht nur als „irgendein“ Primzahlsatz,
sondern als „der“ Primzahlsatz bezeichnet
(wohl weil mit ihm zum ersten Mal eine Regel für das Auftauchen von Primzahlen innerhalb der natürlichen Zahlen bewiesen werden konnte).
Viele Leute kritzeln bei mehr oder minder langweiligen Telefonaten und Sitzungen (auch Vorlesungen und Unterrichtsstunden) auf einem Zettel rum.
(Vgl. etwa
![]() "Die Kritzelei der Woche" und
"Die Kritzelei der Woche" und
![]()
 .)
.)
Und so hat dann auch der bedeutende
Mathematik
![]() Stanisław Ulam
Stanisław Ulam 
1963 mal während eines wissenschaftlichen Vortrags aus Langeweile (drumhe-)rumgekritzelt

 , sondern
, sondern
 hinbekommen, und
dann wäre er vermutlich nie zu der frappierenden Erkenntnis gekommen, um die es gleich
gehen wird.
hinbekommen, und
dann wäre er vermutlich nie zu der frappierenden Erkenntnis gekommen, um die es gleich
gehen wird.(vgl.
(Quelle:
![]() ; Ulams Kritzelei hatte aber vermutlich nichtmal den Zweck, eine Idee zu
finden oder "ein Problem zu stürmen")?
; Ulams Kritzelei hatte aber vermutlich nichtmal den Zweck, eine Idee zu
finden oder "ein Problem zu stürmen")?
(je länger ein Telefonat, ein Vortrag … dauert, desto feiner)
mit feineren Ornamenten gefüllt werden?
(Vgl. oben
| .) |

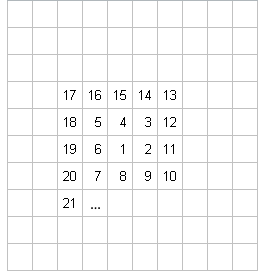 kann man
(konnte wohl auch Ulam) noch nicht erkennen, was hinter den Zahlen
lauert. Sondern der wissenschaftliche Vortrag muss wohl so langweilig
gewesen sein, dass Ulam bis z.B.
kann man
(konnte wohl auch Ulam) noch nicht erkennen, was hinter den Zahlen
lauert. Sondern der wissenschaftliche Vortrag muss wohl so langweilig
gewesen sein, dass Ulam bis z.B.

(oder einfach, bis das Blatt voll war oder dreistellige Zahlen kaum mehr in die Kästchen passten)
weitergemacht hat.
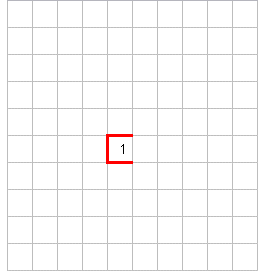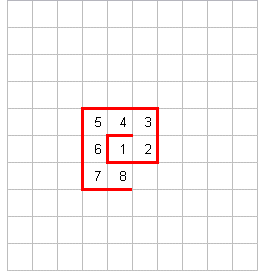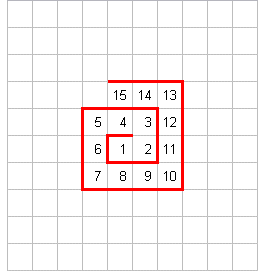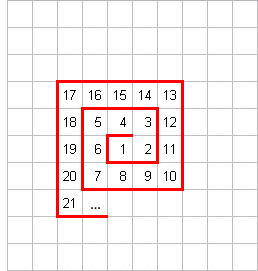 →
→

Das "Aufwickeln" der Zahlen um die
 hat einen enormen
Vorteil: es ist unabhängig vom Zahlensystem
hat einen enormen
Vorteil: es ist unabhängig vom Zahlensystem
(s.o. das Zehner- und Zwölfersystem)
so dass auch vielleicht vorkommende (Primzahl-)Muster unabhängig von diesen Zahlensystemen sind.
(Im Nachhinein bereue ich es, 10 • 10 = 100 Zahlen,
also  genommen und damit doch wieder das Zehnersystem suggeriert zu haben.
Besser
wären da z.B. 8 • 8 = 64 Zahlen, also
genommen und damit doch wieder das Zehnersystem suggeriert zu haben.
Besser
wären da z.B. 8 • 8 = 64 Zahlen, also
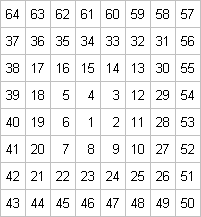 , wobei
keiner an das Achtersystem denken würde; oder vielleicht noch besser
nichtquadratisch, also z.B.
, wobei
keiner an das Achtersystem denken würde; oder vielleicht noch besser
nichtquadratisch, also z.B.
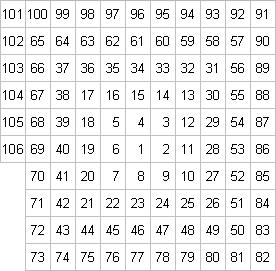 .
.
Entscheidend ist: man kann die Zahlen so oft um die 1 wickeln, wie man lustig ist, also z.B. auch 17,5 mal.)
Wie oben schon gesagt, neigen Leute bei Telefonaten, Vorträgen ... dazu, das anfangs grob erstellte Muster mit immer feineren Ornamenten auszumalen.
Ulam hat dann das feinere Ornament "Primzahlen" gewählt und diese markiert:
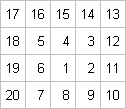 aufgeschrieben
und dann die Primzahlen markiert:
aufgeschrieben
und dann die Primzahlen markiert:
 . Aufgrund der
wenigen (Prim-)Zahlen wäre noch nichts Auffälliges erkennbar gewesen - und
deshalb frage ich mich, ab welchem Zeitpunkt Ulam sein
. Aufgrund der
wenigen (Prim-)Zahlen wäre noch nichts Auffälliges erkennbar gewesen - und
deshalb frage ich mich, ab welchem Zeitpunkt Ulam sein
 -Erlebnis haben
konnte.
-Erlebnis haben
konnte.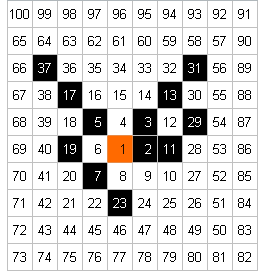 beschlichen haben:
"aller guten Dinge sind drei"
beschlichen haben:
"aller guten Dinge sind drei"
 bzw. "ab drei
scheint etwas eine Regel zu sein":
bzw. "ab drei
scheint etwas eine Regel zu sein":
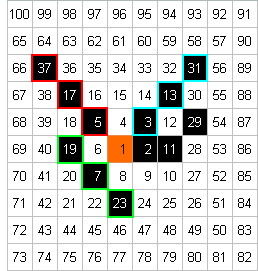 , woran immerhin
schon bemerkenswert ist, dass da auffallend viele Primzahlen auf
diagonalen
Linien liegen.
, woran immerhin
schon bemerkenswert ist, dass da auffallend viele Primzahlen auf
diagonalen
Linien liegen.Wenn hier aber eine strikte Regel vorläge, müssten auch die Zahlen auf den Fortsetzungen der roten, hellblauen und hellgrünen Diagonale Primzahlen sein:
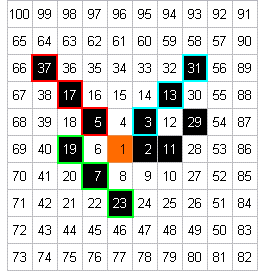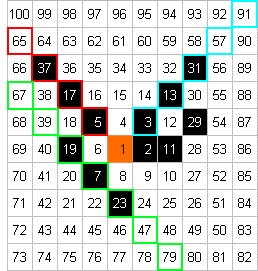
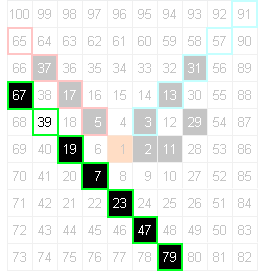
Es klingt erstmal enttäuschend: damit zeigten sich gleichzeitig
In der Mathematik ist eine (vermeintliche) Regel aber keine Regel mehr, wenn sie auch nur eine einzige Ausnahme hat.
(Wohlwollender sind da hingegen der Volksmund mit "Ausnahmen bestätigen die Regel" und Juristen mit "im Zweifelsfall für den Angeklagten".
Nebenbei: auch für die rote Diagonale gilt eine "Regel
mit Ausnahme [65 = 13 •
5]", denn 101 ist wieder eine
Primzahl!:
 )
)
Die ersten hundert natürlichen Zahlen mit den Primzahlen sehen so aus:
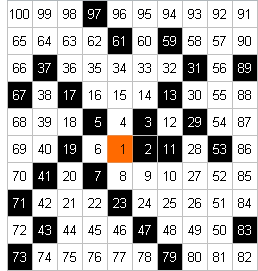
Mag sein, dass auch mal ein Laie stumpf eine Zahlenfolge
auf ein Papier kritzelt. Aber man muss doch (wie Ulam) Mathematiker sein, um
in dieser Zahlenfolge die Primzahlen zu markieren. Und man sollte die in
 vorkommenden Primzahlen (er-)kennen, denn eine Überprüfung aller Zahlen von
1 bis 100 auf mögliche Teiler würden doch den meditativen „flow“ des
Kritzelns zerstören.
vorkommenden Primzahlen (er-)kennen, denn eine Überprüfung aller Zahlen von
1 bis 100 auf mögliche Teiler würden doch den meditativen „flow“ des
Kritzelns zerstören.
Wenn man aber erstmal bei
 ist, kann
vielleicht auch ein Laie das sich andeutende „Diagonalenmuster“ entdecken. Nur
würde er vermutlich sagen: „Ist ja ganz nett, aber was soll‘s?“
ist, kann
vielleicht auch ein Laie das sich andeutende „Diagonalenmuster“ entdecken. Nur
würde er vermutlich sagen: „Ist ja ganz nett, aber was soll‘s?“
Nur ein Mathematiker, der das anscheinend weitgehend chaotische Auftreten der Primzahlen kennt, wird bei einem sich andeutenden Muster ebenso hellhörig wie skeptisch.
Ich kann mir nicht vorstellen, dass Ulam sehr viel mehr als 10 • 10 = 100 Zahlen aufgeschrieben hat. Schon bei 100 • 100 =10.000 Zahlen
hätte der langweilige wissenschaftliche Vortrag unrealistisch lang sein müssen,
wäre ein Blatt Papier zu klein gewesen,
hätte Ulam sicherlich nicht mehr alle vorkommenden Primzahlen erkannt und deshalb tausende sehr umständliche Untersuchungen auf mögliche Teiler durchführen müssen.
Nun lebte Ulam in einer Zeit, in der es kaum Computer gab, um Primzahlen zu berechnen, aber es gab mühsamst erarbeitete Primzahltabellen.
Das Platzproblem ließ sich dadurch lösen, dass man
(wenn es nur um das Muster geht, das die Primahlen bilden, ist es ja uninteressant, welche Primzahl wo liegt).

 .
.
Die Vermutung, dass sich die Primzahlen auf Diagonalen drängeln, scheint sich also zu bestätigen.
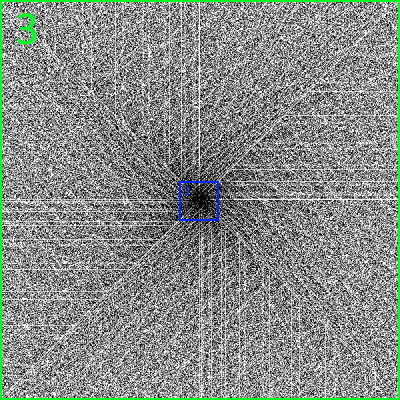 .
.
Daran ist nun dreierlei bemerkenswert:
(nach außen, also für immer größere Zahlen, müsste das Bild immer heller werden);
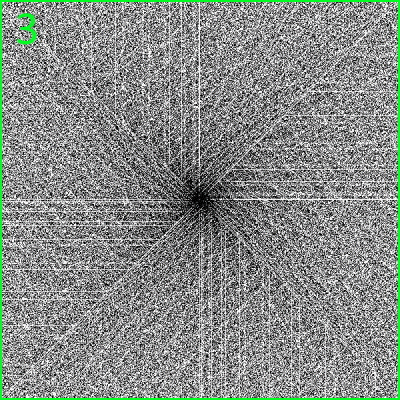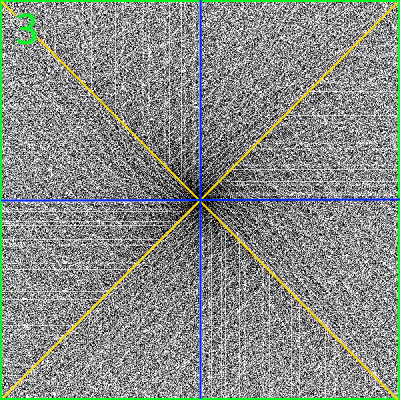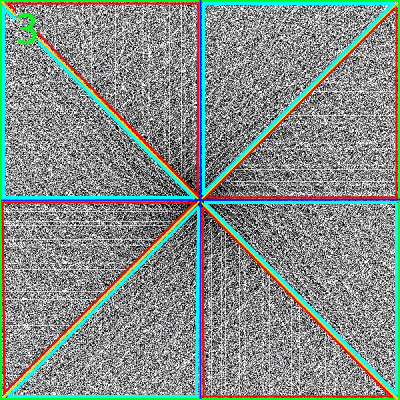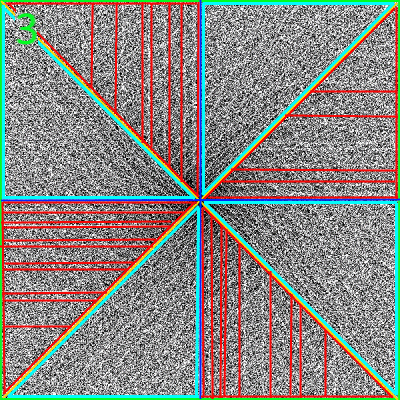 .
.
Wie auch immer: Ulam hat wegen eines glücklicherweise schnarchlangweiligen Vortrags als Erster vermutliche Muster in der Verteilung der Primzahlen gefunden.
Die „Schlange“
 aussehen,
aussehen, aussehen,
womit sich dann dieses Primzahl-Muster ergibt:
aussehen,
womit sich dann dieses Primzahl-Muster ergibt:Und es muss nichtmal eine Schlange, sondern kann auch ein Dreieck sein:

Oder kurz:
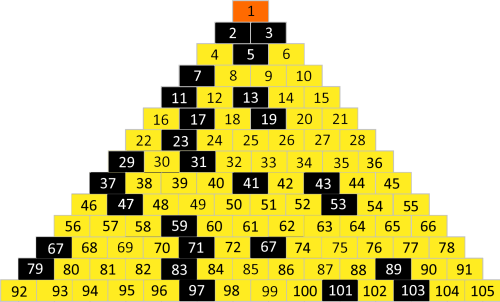
Da fällt es (noch) schwer, ein Muster zu erkennen. Mit sehr viel Phantasie kann man aber vielleicht diese Primzahl-Spalte erkennen
(allerdings wieder mit Ausnahmen, nämlich den zusammengesetzten Zahlen 39 = 13 • 3 und 49 = 7 • 7):
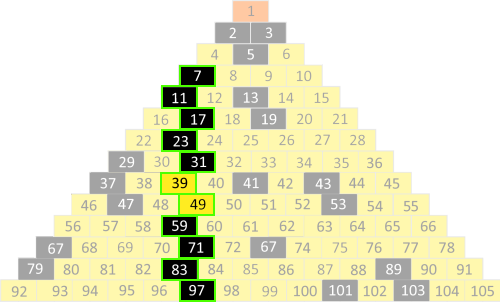
Wenn man aber ein Dreieck mit 1000 Zeilen nimmt, ergibt sich im Vergleich mit Ulams "Schlange" ein sehr viel deutlicheres Primzahl-Muster:
Oder ohne allen Regentropfen-Schnickschnack:

Wenn Ulams Entdeckung 1963 erfolgt ist und auch ziemlich schnell von den
Zahlentheoretikern aufgenommen wurde, kann derzeit, also fast 60 Jahre später,
kaum mehr von
 die Rede sein.
die Rede sein.
„kaum mehr“ impliziert aber „evtl. doch noch ein bisschen“.
„ein bisschen“ sind jene Nicht-Zahlentheoretiker, die erst jetzt von Ulams Spirale erfahren, aIso Laien (Schüler) - und ich.
Ich habe nämlich  überhaupt erst im Jahr 2022 zum ersten Mal gesehen, und das war für mich
überhaupt erst im Jahr 2022 zum ersten Mal gesehen, und das war für mich
(schon wissend, dass da Primzahlen gezeigt werden)
ein regelrechter Erkenntnisschock:
"Diese kleinen Viecher
 [Primzahlen] sind
wirklich raffiniert
[Primzahlen] sind
wirklich raffiniert
und bilden filigrane Muster
 !"
!"
Von wegen "raffiniert":
 liegen besonders viele Primzahlen, aber eben
auch zusammengesetzte Zahlen (hier
weiß);
liegen besonders viele Primzahlen, aber eben
auch zusammengesetzte Zahlen (hier
weiß);
| Warum wusste ich all das bislang nicht, warum hat mir das (auch in meinem Mathematikstudium) keiner gesagt? |