Verteidigung der (Vektor-)Geometrie

Beobachte ich es richtig oder bilde ich es mir nur ein, dass die Geometrie in der Schule seit langem auf dem Rückzug ist? Schließlich möchte ich auch nicht an Pseudoproblemen rumdoktern.

Ein neues Indiz scheint mir, dass in NRW  die Stochastik/Statistik verbindlich gemacht wurde. Weil die Stofffülle aber sowieso schon viel zu groß ist (Masse statt Klasse, sprich Verstehen der zentralen Ansätze), kann das nur bedeuten, dass woanders eingespart bzw. gestrichen wird - und ich vermute doch sehr: in der Oberstufe bei der Vektorgeometrie.

Nebenbei: nichts gegen die Stochastik, die ja auch wichtig ist:

• in vielerlei Anwendungen von der Physik bis zur Sozialwissenschaft
  (und im Tubokapitalismus wird die Schule ja sowieso immer mehr für "Anwendungen" bzw. direkte bis geradezu blindwütige Berufsvorbereitung vereinnahmt);
• rein innermathematisch, weil da eine ganz andere und hochinteressante Denkweise (nämlich die der Wahrscheinlichkeit) ins Spiel kommt.

Dennoch werde ich den Verdacht nicht los, dass immer ca. 15 bis 20 Jahre nach einer Modewelle an der Uni diese zu Schulstoff wird, und zwar deshalb, weil dann die ehemaligen StudentInnEN in kultuspolitische Entscheidungspositionen aufsteigen - und man am liebsten doch das macht, was man mal selbst gelernt hat. Vgl. etwa seinerzeit die Mengenlehre (in der Tat ein fundamentales mathematisches Gebiet!).

Die Geometrie scheint mir aber durchaus wichtig und verteidigenswert, weil

• sie so schön anschaulich

ja teilweise sogar handgreiflich ist - und so hübsch dynamisch (vgl. ),

• anhand ihrer viele mathematische Grundprinzipien und Denkweisen vermittelbar sind,
• sie nunmal im antiken Griechenland der Ursprung aller Mathematik war,
• sie insbesondere (propädeutisch rein äußerlich) ästhetische Erfahrungen ermöglicht (vgl. ).

Insbesondere aber die Vektorgeometrie ist

• nicht nur wichtig
  (vgl. etwa, wie Einstein und Infeld in ihrem Buch  "Die Evolution der Physik" mittels ihrer sehr anschaulich die klassische Physik erklären; und sowieso sind Vektoren die einzige Möglichkeiten, höherdimensionale Räume noch halbwegs zu "erfassen"),
• sondern auch sehr ergiebig
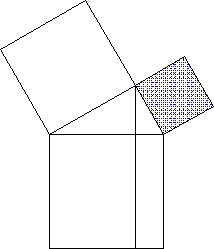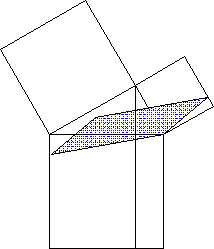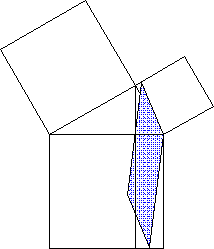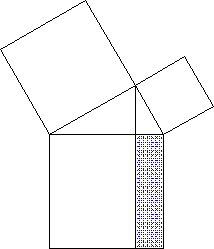
  (vgl. etwa, wie rasant einfach mittels ihrer der Beweis des Satzes der Pythagoras möglich ist)
• sehr anschaulich
• und ungeheuer ästhetisch.

Ein Beispiel:

Zwischen zwei parallelen Ebenen E₁ und E₂ liegt eine Kugel K₁:

Gesucht ist eine weitere zwischen den beiden Ebenen liegende (also gleichgroße) Kugel K₂, die mit K₁ einen Schnittkreis mit einem bestimmten Radius hat:

Schon hier ergeben sich für viele SchülerInnen die ersten Probleme in der angeblich so anschaulichen Vektorgeometrie: Wo, zum Teufel, ist denn der Schnittkreis, von dem in der Aufgabenstellung die Rede ist? K₁ und K₂ sind ja deutlich zu erkennen, aber kein "weiterer" (Schnitt-)Kreis ist vorhanden. Bzw. ich hab´s schon erlebt, dass SchülerInnen durchaus einiges begriffen haben, indem sie in der "Schnittmenge"

einen Kreis bzw. genauer: die Schrägansicht eines Kreises, nämlich eine Ellipse zu entdecken meinten.

Und damit sind wir bei einem zentralen Problem der Vektorgeometrie, sobald sie vom Zwei- ins Dreidimensionale übergeht: zweidimensionale Projektionen (wie etwa an der Schultafel) dreidimensionaler Gegenstände sind wenig hilfreich, da oftmals gar nicht als Projektionen dreidimensionaler Gegenstände erkennbar.

Ich hab´s schon erlebt, dass eine Schülerin in der Oberstufe nicht mal in der Lage war, in

einen (dreidimensionalen) Würfel zu sehen. Nein, sie sah nur zweidimensionale Gegenstände: links unten ein Quadrat und rechts bzw. oben ein Parallelogramm.

Dass das einer ansonsten mathematisch grundsoliden Schülerin passierte, sollte einen hellhörig machen, statt dass man sich leichtfertig "über soviel Blödheit bzw. Blindheit" lustig macht:

1. könnte es ja sein, dass es nicht nur eine sogenannte "Dyskalkulie", d.h. Rechenschwäche

(sozusagen das mathematische Pendant zur Legasthenie, die ja auch nur eine Teilleistungsschwäche ist und keineswegs ganz allgemein von Dummheit oder auch "nur" allgemeiner sprachlicher Unfähigkeit zeugt),

sondern auch eine Schwäche im räumlichen Vorstellungsvermögen gibt - die nichts über sonstige Fähigkeiten in Mathematik besagt.
Das entscheidende Problem besteht hier darin,

1. dass jemand, der das Dreidimensionale in der Kugelaufgabe oben nicht "sieht", nicht die mindeste Chance hat, weiter zu rechnen;

2. dass also letztlich gar keine "richtige" Mathematik, sondern räumliches Vorstellungsvermögen geprüft wird
   (nunja, in Schulfächern wird immer ein "geheimer Lehrplan" mitgeprüft, in Deutsch beispielsweise ganz entscheidend auch sprachliche, emotionale, soziale und historische "Sensibilität").

2. haben auch geübte und gestandene Ingenieure ab und zu Schwierigkeiten, in zweidimensionalen Plänen das geplante dreidimensionale Objekt zu sehen, und dementsprechend unterlaufen ihnen dann manchmal fatale Fehler (z.B. zwei Schrauben, die sich kreuzen). Nicht umsonst gibt es CAD-Programme, die aus zweidimensionalen Projekten "begehbare" dreidimensionale virtuelle Welten erstellen.

3. aber wird man in das Übersetzen von zwei- in dreidimensionale Objekte (und umgekehrt) einführen müssen: (nicht erst) in den (Vektor-)Geometrieunterricht gehören massenhaft dreidimensionale Modelle oder Computeranimationen.
   Erst wenn die Übersetzung vielfach geübt wurde, wird man von SchülerInnen erwarten dürfen, dass sie "im Kopf" aus dem Zwei- auf das Dreidimensionale schließen und im Zwei- das Dreidimensionale "sehen" können.

Manchmal ist es ja so einfach, dreidimensionale Vorstellungen zu vermitteln: es kann SchülerInneN in einer Klausur über Vektorgeometrie nicht untersagt werden, Kanten des Klassenraums als dreidimensionales Koordinatensystem, die Tischplatte als Ebene, eine Stricknadel als Gerade, den Tafelschwamm als Quader und einen (durchgeschnittenen) Apfel als Kugel zu benutzen (Vitamine tun in jeder Klausur gut!).

Ansonsten sagt sich das aber so einfach, dass man "einfach nur" mathematische Modelle oder Programme herstellen sollte. Selbst die simpelsten "Animationen"

(beispielsweise eine Kugel, die sich durch eine Ebene bewegt und dabei mit letzterer verschieden große Schrittkreise bildet)

bereiten da allergrößte mechanische oder programmtechnische Schwierigkeiten. Man bastelt und programmiert halt nicht so einfach und zeitökonomisch, wie man an die Tafel schreibt (die mit gutem Grund Standardillustrationselement im Unterricht ist - und dennoch, wie sich hier exemplarisch zeigt, gefährlich in die Irre führen kann).

Wenn aber einE SchülerIn etwa im Abitur bei der Übersetzung vom Zwei- ins Dreidimensionale stecken bleibt, so wird man ihr/ihm doch immerhin helfen müssen - und zwar mit vorgefertigten Modellen bzw. Computeranimationen.

(Das Problem dabei ist:

• einigen LehrerInneN fehlt die Phantasie und handwerkliche Fähigkeit zu solchen Modellen bzw. Animationen;

• anderen die Phantasie sich vorzustellen, dass SchülerInnen sich sowas Dreidimensionales nicht vorstellen kann; sie wissen einfach schon zu viel - nämlich meistens schon das Ergebnis;

• den allermeisten fehlt [und zwar insbesondere im Abitur- und Klausurstress] aber schlichtweg die Zeit für solch aufwendige Modelle bzw. Animationen.)

Nebenbei: ist es nur ein Zufall, dass der "räumliche Blackout" einer SchülerIN passiert ist? Oder ist was dran am Klischee?:

Männer haben das bessere Orientierungsvermögen
28.02. - Männer haben ein besseres Orientierungsvermögen als Frauen. Das ist das Ergebnis eines Versuchs von Forschern aus Ulm, berichtet die in Baierbrunn bei München erscheinende Zeitschrift "Apotheken Umschau" (Ausgabe 2/2001).

Bei dem Test hatten je zwölf Frauen und Männer aus einem im Computer simulierten Labyrinth herausfinden müssen. Während die Frauen dazu im Schnitt 3 Minuten und 16 Sekunden brauchten, waren die Männer nach durchschnittlich 2 Minuten und 21 Sekunden am Ziel.

Die Forscher vermuten dem Bericht zufolge, dass im Gehirn der Männer noch die Vorzeit-Erfahrung "gespeichert" ist, als Jäger weite Distanzen zu laufen und zur Wohnstätte zurückzufinden 
(Bild der Wissenschaft)

Und was würde es schon besagen, wenn es stimmen würde? Doch nur

1. dass Frauen (und das vermutlich auch nur im Schnitt - damit da nicht nur uralte Männerdomänen legitimiert werden)  in einem Bereich "schlechter" sind - und in anderen Bereichen besser;
2. dass im Vektorgeometrieunterricht eine besondere Sorge den SchülerINNEN zu gelten hätte.

zurück zur Aufgabe oben: der Schnittkreis (in Seitenansicht) sowie sein Radius ergibt sich natürlich folgendermaßen:

(woran man nebenbei auch siehst, dass o.g. falsche "Schnittmenge" durchaus zum richtigen Ziel führen kann)

Und der Abstand beider Kugelmittelpunkte läßt sich dann leicht (wenn man drauf kommt!) mit dem Satz des Pythagoras berechnen.

Des weiteren sei in der Aufgabe gefragt, ob es noch andere Kugeln (Plural, also ein Wink mit dem Zaunpfahl!) gibt, die denselben Schnittkreisradius mit K₁ haben. Eine Antwort, auf die SchülerInnen in der Regel durchaus auch noch kommen, ist natürlich ein Kreis K₃ auf der anderen Seite von K₁:

Danach dann setzt es bei den meisten SchülerInnen aber verlässlich aus, weitere Kugeln "sehen" sie beim besten Willen nicht. Warum?

Doch wohl schlicht und einfach, weil die zweidimensionale Projektion allzu suggestiv ist - also zweidimensional bleibt. Es gelingt den (meisten) SchülerInnen nicht, sie nach vorne und hinten zu erweitern, also zumindest auch eine Kugel vor und eine hinter K₁ zu sehen.

Und schon gar nicht sehen sie unendlich viele Kugeln um K₁ herum bzw. eine Kugel, die um K₁ rotiert

(wobei in dieser illustrierenden Animation allerdings die äußere Kugel die innere nicht mehr schneidet und auch nicht mehr gleich groß ist)

- und zwar (wenn auch nicht maßstabsgetreu: das Loch in der Mitte ist zu groß) in Form eines "Torus" (Schwimmreifens bzw. neudeutsch Doughnut):

Hier zeigt sich nebenbei wieder die Problematik von Modellen: ein vorgefertigtes mechanisches Modell, das den SchülerInneN helfen sollte, würde das Konstruktionsprinzip (die Rotationsachse) ja leider schon vorgeben müssen.

Der Torus ist aber besonders interessant im mathematischen Teilgebiet der Topologie

(u.a. nämlich ein schöner Einstieg in nichteuklidische Geometrie sowie die darauf basierende Relativitätstheorie, in der der Torus ja in der Tat eine Rolle spielt - womit dann am Ende eben doch noch eine "Anwendung" um die Ecke grinst),

die - zumindest ansatzweise - ein wunderschöner Exkurs im Schulunterricht wäre, nämlich auch zur Anschaulichkeit des Dreidimensionalen beitragen könnte. Vgl. z.B. .

Die Aufgabe (die sowieso ohne jeden Anwendungswert ist) wird aber doch überhaupt erst interessant, wenn man derart ins Dreidimensionale und bis hin zum Torus kommt.

Dabei bedeutet "interessant" hier:

1. ästhetisch,

2. mathematisch ergiebig und herausfordernd:
   "Stelle die Gleichung all dieser Kugeln, also einer Kugelschar auf!"

• vgl. die Funktionenscharen in der Analysis;

• und immerhin ist es ja doch erstaunlich - und macht Mathematik u.a. erst aus - , dass man überhaupt eine Gleichung für alle (unendlich viele!) Kugeln aufstellen kann;

• das Kreise im Unterricht üblicherweise nur im Zweidimensionalen definiert wurden, würde es allemal reichen, wenn einE SchülerIn die Grundideen zur Erstellung der Kugelschargleichung angeben würde, d.h. eine Kugelgleichung, in der der Mittelpunksvektor über den Rotationskreis definiert ist:

3. bewegte Mathematik: der Torus ergibt sich durch die Bewegung einer Kugel

(vgl. ).

Ein Torus ist also (u.a.) eine Kugel in Bewegung.

Eine schöne Erweiterung ist es dann nebenbei, den Torus als Ergebnis der Bewegung eines Kreises anzusehen:

Torus [lat.] (Ringfläche, Ringkörper, Kreiswulst), eine Fläche, die durch Rotation eines Kreises um eine in seiner Ebene liegende, den Kreis nicht treffende Gerade entsteht; auch Bez. für den von dieser Fläche begrenzten Körper.

(Meyers Lexikonverlag)

Auch da ergäbe sich eine durchaus anspruchsvolle, ja noch schwierigere Aufgabe (weil der Kreis immer auf den Rotationsmittelpunkt ausgerichtet sein muss): "Erstelle eine Gleichung der Kreisschar!"
(wobei wiederum die Grundideen, d.h. das Erfassen der Problematik wichtig wäre[n], nicht die genaue Formel).

Und dann wäre es natürlich noch reizvoll, aus der Ebene (bzw. aus dem Zwischenraum zwischen den beiden Ebenen E₁ und E₂) heraus ins vollends Dreidimensionale zu gehen, wodurch sich die ergebenden Kugeln (bzw. Kreise) in einer Kugelschale befinden:

Bzw. da umsaust eine Kugel (bzw. ein Kreis) die Kugel K₁ wie die Elektronen den Atomkern:

(wobei das Elektron allerdings nicht nur die wenigen eingezeichneten Bahnen einhält, sondern laut Quantentheorie überall in der Kugelschale "ist")

Wenn man nicht derart dreidimensional wird, bleibt die Aufgabe langweiliges Rechnen und bekommen

• "schlechte" SchülerInnen keinerlei Anschauung,

• "gute" SchülerInnen keinerlei komplexeres "Futter".