Ein Standardthema in der schulischen Vektorgeometrie sind Kugeln bzw. - um genauer, allerdings auch ein bisschen arg altklug zu sein - "Sphären", denn
Eine Sphäre wird vektorgeometrisch beschrieben durch sämtliche "Ortsvektoren" → , die
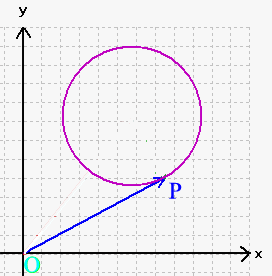
Daraus folgt:
Dabei "beinhalten" die Ortsvektoren natürlich ihre jeweiligen Endpunkte (also alle zusammen die Sphäre), sind aber auch noch mehr, nämlich auch die geraden Wege zu den Endpunkten hin.
In Abwandlung des arg ausgeleierten Spruchs "der Weg ist das Ziel" könnte man also sagen: die Ortsvektoren sind sowohl der Weg als auch das Ziel.
Der Nachteil der Ortsvektoren ist bis hierhin aber, dass sie großteils
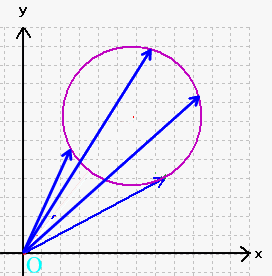
Um da ein bisschen System rein zu kriegen, erinnere man sich, wodurch eine Sphäre grundlegend bestimmt wird, nämlich
Entsprechend zeichnen wir nun zusätzlich den Mittelpunktsvektor →und den "Radiusvektor" → ein:
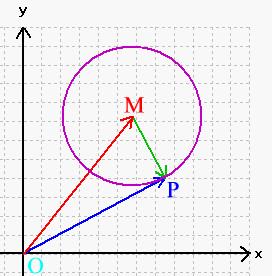
Damit ergibt sich der Ortsvektor als Summe des Mittelpunktsvektors und des "Radiusvektors" :
→ = → + →
Nebenbei: selbstverständlich sind auch andere Mittelpunkte und Radien möglich, also z.B.
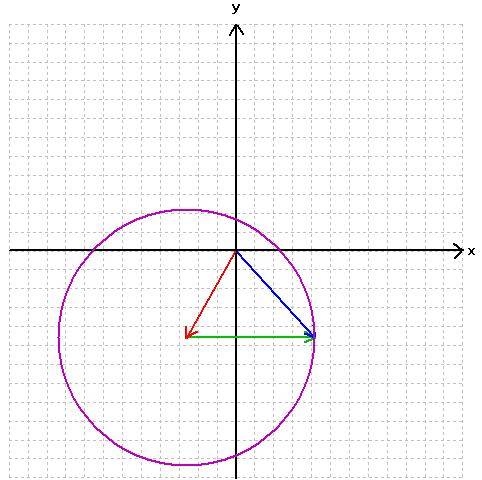
Wenn wir zuerst noch bei einer Kreislinie bleiben, ergibt sich somit:
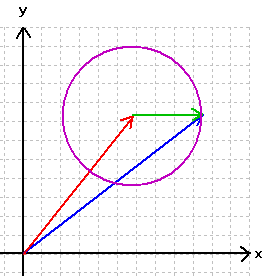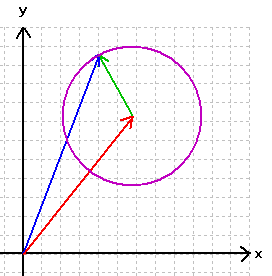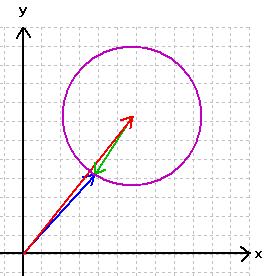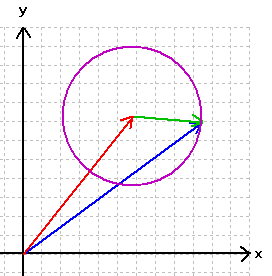
(vgl. das entsprechende Programm in 
)
Daran sollen uns jetzt wiederum erst mal nur die "Radiusvektoren" interessieren. Ihre Bewegung lässt sich wie die eines Uhrzeigers vorstellen
(nur dass dieser andersrum läuft):
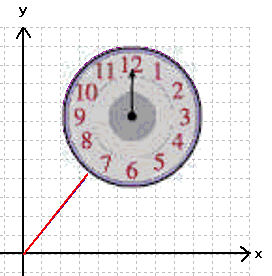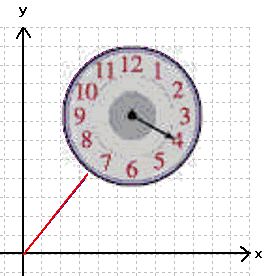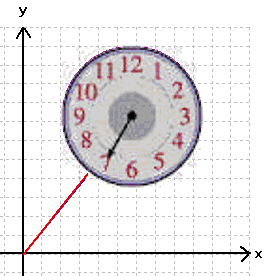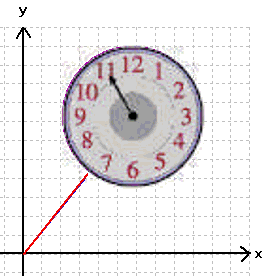
Wenn wir damit aber zur Sphäre übergehen, ergibt sich das Problem, dass sich die "Radiusvektoren"
Eine schöne Vorstellung davon geben aber sogenannte
"Plasmalampen",
die somit nicht nur faszinierend und physikalisch interessant, sondern auch mathematisch "ergiebig" sind:
Oder eine schöne Veranschaulichung bieten auch sogenannte
"Glasfaserlampen":
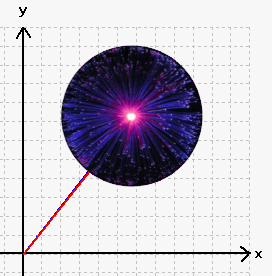
Schöne andere Veranschaulichungen - und es kann ja nicht genug verschiedene solcher Veranschaulichungen für dasselbe "Prinzip" geben:
ein "Koosh"-Jonglierball: 
eine
ein (See-)Igel (vgl. 
)
ein Feuerwerk: 
Kommen wir damit aber zurück zu den Ortsvektoren - und jetzt auch im bei der Sphäre. Es gibt davon zwei Sorten, was sich schön verdeutlichen lässt, wenn man sich
den Ursprung als Sonne 
und die Sphäre als Mond 
vorstellt:
die eine Hälfte der Ortsvektoren/Sonnenstrahlen bescheint die sonnenzugewandte Seite der Sphäre/des Mondes:
die andere Hälfte der Ortsvektoren/Sonnenstrahlen bescheint (arg widernatürlich) die sonnenabgewandte Seite der Sphäre/des Mondes:
Im 1. Fall könnte man auch sagen, alle Ortsvektoren zusammen bilden folgenden massiven Körper:
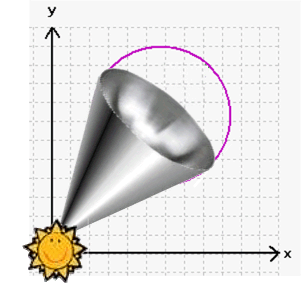
Und im 2. Fall bilden alle Ortsvektoren zusammen folgenden massiven Körper:
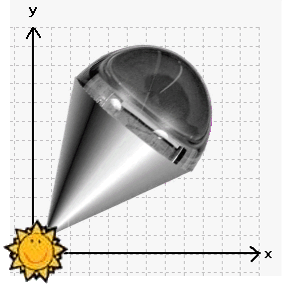
Dabei umfasst der zweite Körper natürlich den ersten, bzw. der erste ist eine Teilmenge des zweiten.
Und wenn man nun den zweiten vom ersten Körper "subtrahieren" wollte, so ergäbe sich merkwürdigerweise die Kugel (also nicht nur Sphäre) bzw.
eine Eiskugel ohne die Waffel
bzw. (noch genauer)
ein halb geschälter Apfel.
Hier ist ein schöner Anlass, die Grenzen meiner Veranschaulichungsversuche aufzuzeigen:
habe ich jahrzehntelang bestens mit "Vektorkugeln" rechnen können, ohne mir jemals so genaue Vorstellungen davon zu machen wie oben;
frage ich mich ernsthaft, ob die anschauliche Vorstellung auch nur im mindesten beim Rechnen hilft - oder sogar ein Irrweg ist.
PS: Die 2D-Alternative für den Vektorkreis:
Lichtscheibe