ätsch, es
geht doch!der Reiz des Verbotenen oder
ätsch, es geht doch!
| Als bei meinem Sohnemann eine Anordnung nicht wirkte, habe ich's einfach verboten. Und siehe da, er hat's sofort getan! |
Zweifelsohne hat die Mathematik den immensen Vorteil, als einzige Wissenschaft gewisse Sachverhalte für alle betroffenen Objekte und endgültig beweisen zu können.
Schauen wir uns einige dieser endgültigen Weisheiten an:
"Alles ist Zahl!" (Pythagoras)
"Die Mathematik ist das Alphabet, mit dem Gott das Universum geschrieben hat!" (Galilei)
"Du sollst keine anderen Götter neben mir haben!"
Durch Null darf man nicht teilen
(und wer's dennoch tut, wird öffentlich ausgekitzelt)!
Aus negativen Zahlen kann (darf) man keine Wurzeln ziehen!
"Kürzen (Wurzel ziehen) aus Summen / tun nur die Dummen!"
Für alle (!) rechtwinkligen Dreiecke gilt der Satz des Pythagoras, also a2 + b2 = c2!
Alle (!) Dreiecke haben eine Winkelsumme von 1800!
Parallelen sind - wie ihr Name schon sagt - parallel, schneiden sich also nie!
Die drei klassischen Probleme
sind nicht lösbar!
Basta!
Es ist nicht (bzw. kaum) zu verhindern, dass die Mathematik da nunmal Recht hat, und doch ist dieses ewige Recht-Haben fatal:
"»Ich habe bemerkt«, sagte Herr K., »dass wir viele abschrecken von unserer Lehre dadurch, dass wir auf alles eine [die endgültige] Antwort wissen.«"
(Bertolt Brecht, Geschichten vom Herrn Keuner)
Ein Beispiel aus meinem jüngsten Unterricht:
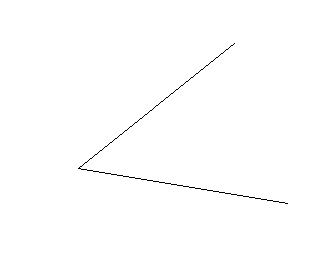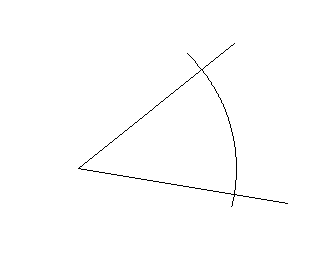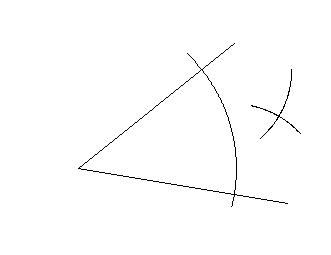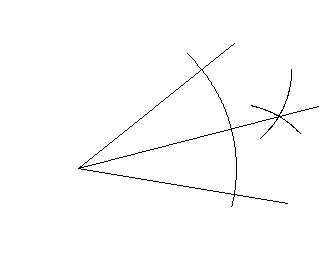
(es würde mich ja doch mal interessieren, warum das hängen geblieben ist - und so vieles anderes nicht);
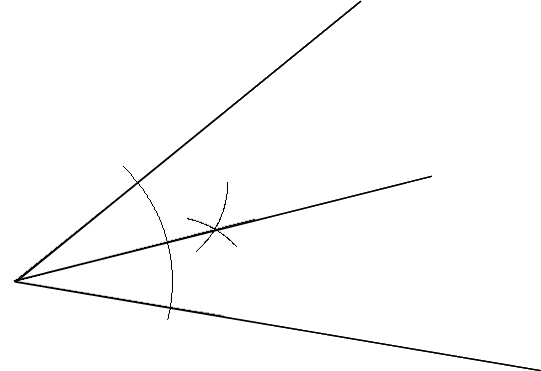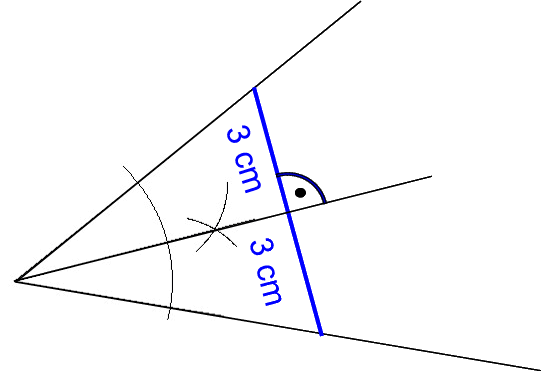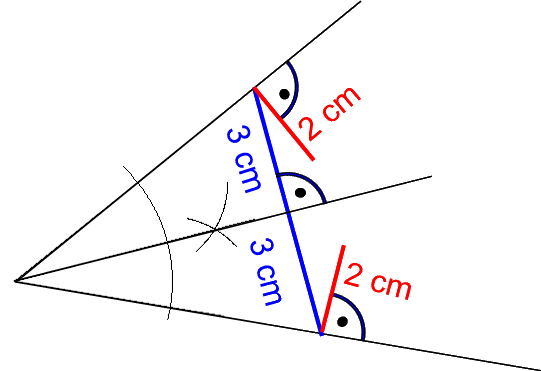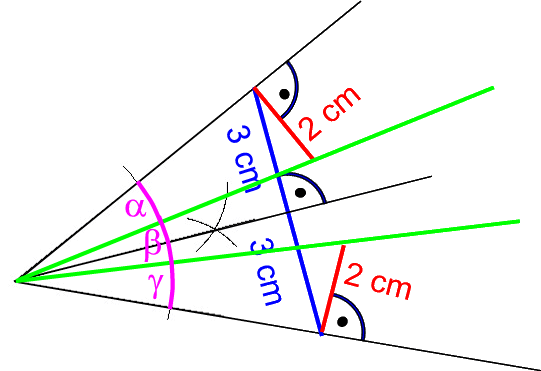
(Egal, ob dieses Verfahren nun richtig war oder nicht, ich finde es immerhin doch raffiniert!)
Behauptet wurde also, dass dabei die drei Winkel α, β und γ gleich groß seien, und Nachmessen ergab tatsächlich sehr ähnliche Werte. Darauf folgte dann eine interessante Diskussion, ob die (wenn auch geringe) Abweichung von exakter Gleichheit
Schnell wurde allerdings anhand anderer (größerer) Ausgangswinkel klar, dass a. der Fall war, also kein genaues Winkeldreiteilungsverfahren gefunden worden war.
Die Zeichnung
selbst scheint hingegen zu komplex zu sein, als dass SchülerInnen bereits daran erkennen konnten, dass wohl α und β gleich groß sein mussten, aber nicht auch γ gleich groß sein konnte.
Schlimm war hingegen meine eigene erste Reaktion auf den Schülervorschlag: ich wusste ja, dass die Winkeldreiteilung nicht möglich ist, und deshalb habe ich mir erst gedacht:
"Lass' ihn konstruieren, es ist ja sowieso falsch, und also brauchst du dir die Konstruktion gar nicht genauer ansehen."
Erst als der Schüler hartnäckig nachfragte, wieso seine Konstruktion denn falsch sei, obwohl sie doch drei annähernd gleiche Winkel ergab, war ich gezwungen, auf seine konkrete Konstruktion einzugehen. Und da konnte ich ja nicht einfach sagen, dass längst bewiesen sei, dass die Winkeldreiteilung unmöglich ist.
Kommt hinzu, dass dieser Beweis (vgl. etwa 
) ja für den Schüler sowieso zu schwierig wäre - und ich ihn auch nicht kannte (verstehen würde?).
(Ein Hinweis von Felix Lenders:
Sie schreiben, dass Sie den Beweis der Unmöglichkeit der Winkeldreiteilung mit Zirkel und Lineal nicht kennen würden und ihn bei Kenntnis evtl auch nicht verstehen würden. Ich wollte hier nur kurz einhaken falls Sie das schöne Buch von Richard Courant und (Anthony?) Robbins noch nicht kennen: In dem nun ca. 60 Jahre alten Buch 
dieser Autoren wird auch diese Frage sehr verständlich beantwortet. Der Ansatz des Buches ist die Titelfrage dadurch zu beantworten, einfach Mathematik (Themengebiete bis zu Oberstufenniveau und ein wenig darüber hinaus) zu machen. Die Darstellung ist stilistisch relativ nah an normalen Lehrbüchern angelehnt und (zumeist innermathematisch) sehr motiviert, die Verständlichkeit sehr hoch.")
Fast habe ich ja sogar die Einstellung: der Beweis, dass etwas nicht möglich ist, interessiert mich auch gar nicht. Sondern wenn "die Mathematiker" es bewiesen habe, glaube ich es einfach.
(Um solch eine Einstellung geht für viele Leute sogar kein Weg drumherum: sie haben zu wenig mathematische Ahnung, um den Beweis, dass etwas nicht funktioniert, zu verstehen, und versuchen dann aussichtslos, es dennoch zu beweisen. Vgl. nur die vielen unsäglichen [auch ihrerseits völlig unverständlichen] Versuche, eine Quadratur des Kreises hinzubekommen: 
)
Überhaupt kann man sich fragen, ob es pädagogisch sinnvoll ist, den SchülerInneN unlösbare Aufgaben zu geben
(bzw. solche, von denen der Lehrer vorher schon weiß, dass sie unlösbar sind):
So oder so ist aber die Einstellung "ich weiß es allemal besser und brauch's nicht mal zu beweisen" indiskutabel.
Es ist letztlich eine Frage der Autorität:
Letztere Autorität kann nur vermittelt werden, wenn man selbst (der Lehrer) sehr demütig ist: "Ich verstehe den Beweis auch nicht oder müsste mich doch erstmal sehr lange einarbeiten."
Man vergibt sich nichts, wenn man anerkennt, dass es (zumindest in der Spezialisierung) größere Geister als einen selbst gibt.
Nun haben aber fast alle oben genannten "Zehn Gebote" einen Haken, nämlich oftmals trotz des Allgemeinanspruchs
(z.B. "Alle Dreiecke haben eine Winkelsumme von 1800!")
einschränkende Nebenbedingungen, die allerdings oftmals gar nicht mehr ausdrücklich erwähnt werden.
Beispielsweise gilt die Winkelsumme 1800 "nur" in der Ebene, also eben doch nicht für alle Dreiecke. Z.B. ist die Winkelsumme
(vgl. 
)
Aber diese Erweiterung auf Kugel und Sattel scheint ja ihrerseits schon wieder spitzfindig-besserwisserisch zu sein. Der "Normalfall" ist doch wohl die Ebene, und deshalb waren auch Mathematiker lange Zeit nicht bereit, Kugel- und Sattelflächen und damit eine anders geartete (riemannsche) Geometrie als ernsthafte mathematische Gegenstände zu akzeptieren.
Nun gibt es aber zu fast jedem der oben genannten "Zehn Gebote" eine einschränkende Nebenbedingung:
(auch auf den ersten Blick wieder derart spitzfindig, dass sogar Mathematiker sich lange Zeit dagegen gewehrt haben)
über die reellen Zahlen hinaus geht und die komplexen Zahlen zuläßt; man kann also durchaus, was in der Schule andauernd mit erhobenem Zeigefinger verboten wird.
entstehen, wenn Gott [in seiner unendlichen Machtfülle dann doch] durch null teilt."Es lohnt sich also allemal (ist mathematisch enorm produktiv), wenn man das Verbotene tut. Nur darf man es nicht einfach "frei Schnauze" tun, sondern sollte sich genau die einschränkenden Nebenbedingungen anschauen und diese aushebeln.
Das Problem dabei ist allerdings heutzutage, dass die einschränkenden Nebenbedingungen wohl nur noch aushebeln kann, wer in allermodernster, fortgeschrittenster Mathematik fit ist - womit sämtliche Laien, SchülerInnen und auch "kleine" MathelehrerInnen von einer aktiven Beteiligung am mathematischen Fortschritt ausgeschlossen sind.
Es bleiben die drei klassischen Probleme
die ja eigentlich weitgehend belanglos sind bzw. an denen nur interessant ist, dass sie nicht lösbar sind.
Natürlich kannte ich die einschränkende Nebenbedingung für diese Probleme, nämlich dass die Konstruktion mit Zirkel und Lineal durchgeführt werden muss.
Für diese Einschränkung "mit Zirkel und Lineal" gibt es natürlich gute Gründe, stehen Zirkel und Lineal doch für die Idealformen Kreis (perfekt rund) und Gerade (wie das Wort schon sagt: gerade).
(Nebenbei: der Aberwitz der Beweise, dass die drei klassischen Probleme nicht mit Zirkel und Lineal lösbar sind, liegt darin, dass diese Beweise nicht geometrisch, sondern algebraisch geführt werden, obwohl die ursprüngliche Aussage doch jeweils geometrisch ist. Und genau das verführt wohl so viele Sonderlinge zu dem aussichtslosen Versuch, die Beweise dennoch [und zwar geometrisch] zu führen, zumal sie die algebraischen Beweise ja sowieso nicht verstehen.)
Obwohl ich also die "kleine", aber doch allzu selten mitgenannte Einschränkung "mit Zirkel und Lineal" kannte, war ich bis vor kurzem dennoch der Meinung, dass die drei klassischen Probleme grundsätzlich nicht lösbar seien, also auch nicht auf anderen Wegen als mit Zirkel und Lineal.
Wie überrascht war ich dann aber - und wie sehr habe ich mich dann doch reingelegt gefühlt, als ich erfuhr, dass zumindest die zwei Probleme "Winkeldreiteilung" und "Würfelverdopplung" sehr wohl anderweitig gelöst werden können, nämlich
.(... und überhaupt steht Origami vielleicht ein wenig im Ruf kleinkarierten Bastelns - und ist es doch allemal wert, Einzug in den Matheunterricht zu halten;
Nebenbei: ich habe die Origami-Lösungen nicht auf Richtigkeit überprüft - und frage mich gleichzeitig, ob nicht auch mit Zirkel und Lineal nachkonstruiert werden kann, was im Origami gefaltet wird; ob die beiden Probleme dann auf diesem Umweg eben doch mit Zirkel und Lineal lösbar wäre, was ja aber nicht sein kann.
Kleiner Zusatz, ums spannend zu machen:
"Nach einer Legende befragten die Bewohner der Insel Delos während einer Pestepidemie 430 v. Chr. das Orakel von Delphi um Rat. Dort wurden sie aufgefordert, den würfelförmigen Altar im Tempel des Apollon im Volumen zu verdoppeln. Für antike Mathematiker bedeutete dies, dass die Seitenlänge eines Würfels mit dem doppelten Volumen unter ausschließlicher Verwendung von Zirkel und Lineal konstruiert werden sollte."
[zitiert nach ])
Da würde es mich nicht wundern, wenn auch die 
Quadratur des Kreises mit anderen Mitteln als Zirkel und Lineal möglich wäre.
(Ich bin da zumindest bislang noch nicht fündig geworden.)
Wenn aber die mathematische Quadratur des Kreises dennoch möglich wäre, hätte das Folgen weit über die Mathematik hinaus, denn die Quadratur des Kreises ist ja der Inbegriff des auch ansonsten Unmöglichen. Dann also gäbe es
(und das würde mich doch diebisch freuen!)
rein gar nichts mehr, was grundsätzlich unmöglich wäre. Vgl. etwa 
.