Mathematik hübsch verpacken

Laien (Schüler) stellen sich das oftmals so vor: Schulbuchautoren bzw. Lehrer rechnen massenhaft Aufgaben durch, bis sie darunter endlich eine finden, die zu "soliden" = einfachen Ergebnissen führt, und diese eine Aufgabe wird dann den Schülern zum Fraß (Lösen) vorgeworfen.

("einfache Ergebnisse", weil

• diese für Schüler ein Signal sind, dass diese Ergebnisse auch richtig sind

[obwohl natürlich auch ein schwieriges Ergebnis richtig sein kann],

• dann vermutlich auch der Weg zu diesen einfachen Ergebnissen hin einfach ist, die Schüler also nicht überfordert werden.

[Ich finde allerdings Aufgaben faszinierender, die

• nach schwierigen Rechnungen
• erstaunlicherweise dennoch zu einfachen Ergebnissen "zusammenschrumpfen",
  

womit sich die Frage stellt, warum am Ende doch ein einfaches Ergebnis rauskommt - und ob man das vielleicht sogar von Anfang an hätte sehen können: die Rechnungen sind ja manchmal schlauer als man selbst].)

Aber die Schulbuchautoren bzw. Lehrer sind natürlich viel zu faul

(und haben dazu auch gar keine Zeit),

massenhaft Aufgaben durchzurechnen, bis sie die eine brauchbare finden (oder eben auch nicht).

Sondern umgekehrt wird ein Schuh draus:

Schulbuchautoren bzw. Lehrer

• fangen mit den erwünschten (einfachen) Ergebnissen an

(kennen sie also von Anfang an),

• verpacken diese dann in Aufgaben, die
• dann den Schülern vorgelegt werden, die
• dann mühsam jene Ergebnisse herausfinden müssen,
• welche die Schulbuchautoren bzw. Lehrer von Anfang an kannten:

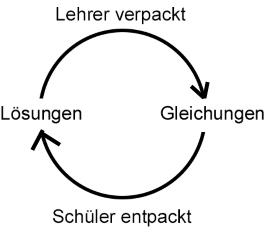
Solches Vorgehen

(etwas kompliziert machen, damit ein anderer es mühsam wieder einfach macht)

hat aber etwas unnötig Umständliches, ja, Hinterhältiges an sich, und es erinnert mich

• an Puzzles , für die fertige Bilder zerstanzt werden, damit andere sie wieder mühsam zusammensetzen

(ich werde nie verstehen, was daran Spaß machen soll: für mich ist das stumpfe Beschäftigungstherapie und eine Idiotentätigkeit bzw. Sträflingsarbeit, für andere aber wohl eine Meditationsform);

• Schaschlik , bei dem der Metzger bzw. Koch einzelne Fleischstücke und sonstige Zutaten (Zwiebeln, Paprika) mühsam aufspießt, damit der Kunde bzw. Gast sie noch mühsamer wieder abpuhlt - und sich dabei ggf. das Hemd versaut.

Für Lehrer hat es aber enorme Vorteile, die Ergebnisse von Anfang an zu kennen: beim Korrigieren von Klassenarbeiten können sie die Rechenergebnisse der Schüler sofort anhand der bereits bekannten Lösungen überprüfen.

(Und es gibt ja überarbeitete oder sowieso verantwortungslose Lehrer, die sich

• überhaupt nur dafür interessieren, ob Schüler komplett richtig gerechnet haben,
• nicht aber für die Rechenwege hin zu vielleicht falschen Ergebnissen:

so muss der Lehrer

• eben nur schnell die Ergebnisse überprüfen

[die Klassenarbeiten also gar nicht ganz lesen],

• aber nicht umständlich die gesamten Rechenwege der Schüler überprüfen, was auch heißen würde, dass der Lehrer äußerst mühsam mit Rechenfehlern der Schüler weiterrechnen müsste, um zu überprüfen, ob die Schüler mit solchen Rechenfehlern immerhin richtig weitergerechnet haben: was zur Konsequenz haben kann, dass der Lehrer massenhaft Aufgaben vieler Schüler komplett nochmals rechnen muss

[womit man vielleicht eine Ahnung davon bekommt, wieviel Arbeit in der Korrektur eines Klassensatzes Mathematikarbeiten stecken kann].)

Dass Schulbuchautoren bzw. Lehrer die (meist einfachen) Ergebnisse von Anfang an kennen und dann nur noch in Aufgaben verpacken, hat aber auch einen Nachteil: weil die Lehrer die Aufgaben nicht genauso rechnen wie die Schüler, merken die Lehrer evtl. gar nicht, wie aufwendig die Rechnungen sind, die dennoch zu einfachen Ergebnissen führen:

Lehrer sollten also zumindest bei Klassenarbeiten alle Aufgaben dringend vorher genauso rechnen wie die Schüler, also sozusagen "von hinten".

Wie aber funktioniert das Verpacken bereits bekannter Aufgabenergebnisse? Das sei mal an einigen Aufgabe zum Lösen von "2 Gleichungen mit 2 Unbekannten" vorgeführt:

1. : ein Gleichungssystem aus "2 Gleichungen mit den 2 Unbekannten x und y" hat üblicherweise folgende Form:

     a•x +         b•y = c
    d•x +         e•y = f,

wobei a, b, c, d, e und f beliebige Zahlen sind, also z.B. a = 17, b = 3,4, c = -24, d = 509, e = 72,15 und f = - , womit sich ergibt:

   17•x +      3,4•y = -  24
509•x + 72,15•y = -

Dabei lassen allerdings die schwierigen Zahlen vermuten, dass nicht nur der Rechenweg schwierig sein wird, sondern auch komplizierte

(und damit falsch aussehende)

Ergebnisse für x und y herauskommen

(und in der Tat sind die [vollständig gekürzten!] Lösungen

• x = oder ungefähr - 5,95,
• y = oder ungefähr 22,69

nicht gerade einfach).

Auch Lehrer würden solch eine Aufgabe wohl ungern rechnen - und sollten also damit auch nicht Schüler quälen.

Nehmen wir also einfachere Zahlen, nämlich z.B. a = 3, b = 4, c = 5, d = 6, e = 7 und f = 8, womit sich ergibt:

3•x + 4•y = 5
6•x + 7•y = 8

Das sieht nun viel einfacher aus, aber wir können uns dennoch nicht sicher sein, dass auch für x und y einfache (ganzzahlige) Ergebnisse herauskommen. Und in der Tat ergibt sich

(ich spare es mir mal, hier die ganze Rechnung vorzuführen)

zwar für y die einfache (natürliche) Zahl 2, für x aber der "komplizierte" Bruch .

(Nunja, so kompliziert ist nun auch wieder nicht

[zumindest nicht für Lehrer],

aber dennoch ist solch ein Ergebnis ablenkend, wenn es um das grundlegende Verständnis der Lösung von Gleichungssystemen geht.

Und auch in Klassenarbeiten zum Thema "Gleichungssysteme" sollten - zumindest anfangs - sehr einfache Gleichungssysteme vorkommen:

1. damit die Schüler überhaupt erstmal einen geglückten Start hinlegen und somit Selbstvertrauen gewinnen,
2. aber, was oftmals übersehen wird: damit sie beweisen können, dass sie das neue Thema "Gleichungssysteme" beherrschen, ohne dass es schon durch überflüssigen [uralten] Schnickschnack erschwert wird:

wenn ein Lehrer immer alten und neuen Stoff mixt, wird er nie merken, wo denn nun die eigentlichen Schülerprobleme liegen.

[Es ist wie mit der alten Regel "drehe (z.B. wenn der Automotor nicht funktioniert) nie an zwei Schrauben gleichzeitig (denn so wirst du eventuell nie bemerken, an welcher der beiden Schrauben es liegt, oder alles sogar noch verschlimmbessern)".]

Und ich befürchte, dass viele Schüler in Klassenarbeiten nur deshalb scheitern, weil sie uralte Probleme

[z.B. mit der Bruchrechnung oder Termumformungen]

mitschleppen, obwohl sie den neuen Stoff durchaus beherrschen.

Mit all dem möchte ich natürlich nicht sagen, dass man alten Stoff völlig ausblenden sollte

[was oft zur Folge hat, dass die Schüler im besten Fall immer nur den gerade aktuellen Stoff beherrschen - und direkt nach der zugehörigen Klassenarbeit wieder vergessen].

Aber ich würde halt trennen:

Und obwohl die Lösung der zweiten Aufgabe schwieriger wäre und mehr Zeit in Anspruch nähme, gäbe es für beide Aufgaben doch gleich viele Punkte.

[Nebenbei: ist eigentlich schonmal jemandem aufgefallen, dass "schlechte" Schüler in der Mathematik oftmals doppelt bestraft werden?:

1. verrechnen sie sich oft, was sowieso schon erste Punktabzüge setzt,
2. müssen sie dann mit den falschen und oftmals schwierigeren Zwischenergebnissen
weiterrechnen

[da kann eine ursprünglich einfache Aufgabe dann schnell teuflisch schwierig oder sogar unlösbar werden]

und brauchen dafür erheblich mehr Zeit, die ihnen evtl. später für Folgeaufgaben fehlt. Das sorgt dann schnell für weitere Punktabzüge,

sodass insgesamt durch einen einzigen Rechenfehler die Punktzahl schnell geviertelt wird.])

Zurück zu dem doch schon relativ einfachen Gleichungssystem

3•x + 4•y = 5
6•x + 7•y = 8,

das die einfache Lösung y = 2 und die nicht mehr ganz so einfache Lösung x =  hat.

Nun könnten Schulbuchautoren bzw. Mathematiklehrer natürlich andere einfache Zahlenwerte für a bis f ausprobieren, aber wenn sie Pech haben, finden sie erst nach langem Probieren einfache Zahlenwerte für a bis f, die auch zu einfachen Lösungen für x und y führen - oder sie finden in halbwegs vertretbarer Zeit überhaupt keine günstige Kombination.

Solches Rumprobieren ist Mathematikern aber zu unsicher, und da dabei evtl. auch enorm viel Zeit draufgeht

(immerhin muss für jede Kombination von Zahlen für a bis f jeweils ein Gleichungssystem gelöst werden),

sind die Mathematiker auch zu faul dazu.

Sie suchen daher nach einem totsicheren System zur Erstellung

• einfacher Gleichungssysteme
• mit einfachen Lösungen für x und y.

Dazu fangen wir z.B. mit den besonders einfachen Wunschlösungen x = 1 und y = 2 an. Wir setzen1 für x für 2 für y in die beiden Gleichungen

3•x + 4•y = 5
6•x + 7•y = 8

ein und erhalten

3•1 + 4•2 = 5
6•1 + 7•2 = 8 ,

was vereinfacht

3 +   8 = 5
6 + 14 = 8

und noch einfacher

11 = 5
20 = 8

ergibt.

Beide Gleichungen sind plötzlich falsch, d.h. x = 1 und y = 2 sind eben doch nicht (wie gewünscht) Lösungen der beiden Gleichungen

3•x + 4•y = 5
6•x + 7•y = 8 .

Das hätten wir natürlich auch schon vorher wissen können, denn uns war ja bereits bekannt, dass x = und y = 2 die beiden einzigen Lösungen des Gleichungssystems

3•x + 4•y = 5
6•x + 7•y = 8

sind.

Damit die Gleichungen dennoch "stimmen", setzen wir auf der rechten Seite

• für c statt 5 nun 11 und
• für f statt 8 nun 20

ein und erhalten das Gleichungssystem

3•x + 4•y = 11
6•x + 7•y = 20 ,

und siehe da, x = 1 und y = 2 sind tatsächlich die Lösungen dieses neuen Gleichungssystems

3•x + 4•y = 11
6•x + 7•y = 20 ,

denn wenn wir in dieses x = 1 und y = 2 einsetzen, erhalten wir

3•1 + 4•2 = 11
6•1 + 7•2 = 20

und einfacher die offensichtlich richtigen Aussagen

3 +   8 = 11
6 + 14 = 20.

Auf diese Weise können wir nun beliebig viele Gleichungssysteme mit Wunschlösungen bekommen. Nur ein weiteres Beispiel:

a•x + b•y = c
d•x + e•y = f

an und wählen z.B. a = 1, b = 2, d = 3 und e = 4

(aber noch nicht Zahlen für c und f!).

Damit erhalten wir

1•x + 2•y = c
3•x + 4•y = f .

1•x + 2•y = c
3•x + 4•y = f

für x die 5 und für y die 6 ein und erhalten

1•5 + 2•6 = c
3•5 + 4•6 = f ,

also einfacher

   5 + 12 = c
15 + 24 = f

und noch einfacher

17 = c
39 = f .

Wenn wir nun 17 bzw. 39 für c bzw. f  in

1•x + 2•y = c
3•x + 4•y = f

einsetzen, erhalten wir

1•x + 2•y = 17
3•x + 4•y = 39 .

• Dieses Gleichungssystem mit immer noch sehr einfachen natürlichen Zahlen können wir nun aber an die Schüler weiterreichen:

• sie müssen dann mühsam wieder die beiden (allerdings einfachen) Lösungen x = 5 und y = 6 berechnen,
• während wir diese beiden Lösungen längst kennen.

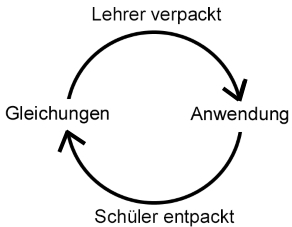
2. : damit die Schüler nun auch noch bemerken, dass Gleichungssysteme nicht bloß innermathematischer Selbstzweck , sondern auch ungemein anwendungsrelevant sind, müssen die Gleichungssysteme nun noch hübsch in mehr oder minder realistische Anwendungen verpackt werden.

Das funktioniert üblicherweise so: man nehme irgendein (rein mathematisches) Gleichungssystem, also z.B. das bereits oben erarbeitete Gleichungssystem

1•x + 2•y = 17
3•x + 4•y = 39 ,

von dem wir schon wissen, dass seine Lösungen x = 5 und y = 6 sind. Nun müssen wir nur noch für x außermathematische Bedeutungen finden

(dabei sollten die Lösungen x = 5 und y = 6 in der jeweils gewählten Anwendung halbwegs realistische Größenordnungen haben).

Zwei Beispiele:

1. x = Preis einer (einzigen) Packung Kakao,
   y = Preis einer (einzigen) Packung Kaffee.

Die zugehörige Aufgabe könnte dann etwa folgendermaßen lauten:

"Erna kauft eine Packung Kakao und zwei Packungen Kaffee für insgesamt 17 €.
Karl kauft drei Packungen Kakao und vier Packungen Kaffee für insgesamt 39 €.
Wieviel kostet eine (einzige) Packung Kakao und wieviel kostet eine (einzige) Packung Kaffee?"

Läßt man nun den Anwendungsbezug wieder weg, so ergibt sich als die dahinter liegende Mathematik

1•x + 2•y = 17
3•x + 4•y = 39

Da sind (wie wir bereits wissen) x = 5 und y = 6 die innermathematischen Lösungen, und wenn man diese in die Anwendung rückübersetzt, so ergibt sich die Antwort

"eine Packung Kakao kostet 5 € und eine Packung Kaffee kostet 6 €".

2. : derzeit werden wie wohl nie zuvor die Innenstädte durch grausige "Investorenarchitektur" verschandelt:

Diese "Investorenarchitektur" zeichnet sich durch zwei Eigenschaften aus:

• phantasielose Aneinanderreihung von Rechtecken

(dazu bedarf es ja eigentlich keines Architekten),

• möglichst billige Bauweise

(der Schrott soll ja auch nicht länger als 30 Jahre halten).

Aber immerhin sollen diese Bauten "untenrum" etwas hermachen, weshalb insbesondere die Eingangshallen immer imposant einschüchternd (aseptisch leer!) sind

und vielleicht auch noch die untersten Stockwerke ein wenig aufwendiger gestaltet werden, während darüber

(trotz eventuell spektakulärer, also kurzfristig "witziger" Fassade ; man spricht dann neuerdings unisono von einem "markanten Entrée" in die Stadt)

nur noch platzsparend die Angestellten gestapelt werden:

Um aber auch die untersten, großzügigeren Stockwerke dennoch möglichst preisgünstig bauen zu können, hat die Firma "jas [junk architecture solutions]" nun ein Fertigbausystem aus zwei verschieden hohen Stockwerkmodulen entwickelt:

"Ein Stockwerkmodul A und zwei Stockwerkmodule B sind insgesamt 17 m hoch.
Drei Stockwerkmodule A und vier Stockwerkmodul  B sind insgesamt 39 m hoch.
Wie hoch ist ein (einziges) Stockwerkmodul A und wie hoch ein (einziges) Stockwerkmodul B?"

Wenn man nun x = Höhe eines Moduls A und y = Höhe eines Moduls B definiert und nun auch hier den Anwendungsbezug wegläßt, so ergibt sich als die dahinter liegende Mathematik ebenfalls wieder unser altbekanntes Gleichungssystem

1•x + 2•y = 17
3•x + 4•y = 39

Da sind (wie wir bereits wissen) x = 5 und y = 6 die innermathematischen Lösungen, und wenn man diese in die Anwendung rückübersetzt, so ergibt sich die Antwort

"ein Stockwerkmodul A ist 5 m hoch und ein Stockwerkmodul B ist 6 m hoch".

Und so lassen sich massenhaft "Anwendungsbeispiele" zu immer demselben Gleichungssystem

1•x + 2•y = 17
3•x + 4•y = 39

finden.

Bemerkenswert an den beiden Beispielen "Kakao-/Kaffeepackungen" und "Stockwerksmodule"

(und beliebig vielen anderen zu demselben Gleichungssystem)

ist es ja doch, dass da

• zwar zwei bzw. beliebig viele (scheinbar) völlig unterschiedliche Anwendungsprobleme
• aber allesamt auf dasselbe Gleichungssystem reduzierbar sind.

Gerade diese universelle Anwendbarkeit

• ein und desselben Lösungsverfahrens
• auf verschiedenartigste Anwendungsbeispiele

ist ja eine der merkwürdigsten Fähigkeiten der Mathematik, bzw. die Mathematik besteht ja zu einem gerüttelt Maß darin, aus unterschiedlichsten Anwendungen die wenigen Reste herauszudestillieren, die diese Anwendungen überhaupt gemeinsam haben.

Diese minimalen Gemeinsamkeiten sind nun aber nur die mathematischen:

• zum Kakao-/Kaffeebeispiel:

• die beiden einkaufenden Menschen könnten statt Erna & Karl genauso gut Max & Moritz, Hennes & Mauritz oder Tim & Struppi heißen, und genauso gut könnte nur eine Person namens Hasso heute 12 Kaffee-, morgen aber 3 Kakao- und 4 Kaffeepackungen kaufen; überhaupt sind die Personennamen für das Kakao-/Kaffee-Problem völlig nebensächlich, man könnte sie also auch problemlos weglassen oder die Personen einfach X und U nennen;

• obwohl es beispielsweise einem notorischen Kaffeetrinker keineswegs egal sein wird, ob versehentlich Tee statt Kaffee gekauft wird, könnte in der Aufgabe genauso gut von Sojamilch- & Tee-, aber auch von Mehl- & Zementpackungen die Rede sein

(obwohl es völlig widersinnig erscheint, dass Leute gleichzeitig Mehl und Zement einkaufen):

die Namen der Produkte spielen also genauso wenig eine Rolle wie die Namen der einkaufenden Personen, d.h. wir könnten auch die Produktnamen weglassen oder die Produkte einfach Schlamp & Pamp nennen.

ebenso unwichtig ist es, ob die Ergebnisse in Dollar oder Cents oder Euro oder -Scheinen bezahlt werden

(Hauptsache, dass sowohl die Kakao- als auch die Kaffeepackungen in derselben Einheit bezahlt werden).

"Unwichtig" ist die Frage, in welcher Einheit bezahlt wird, aber nur in mathematischer Hinsicht. Für jeden Einkaufenden macht es nämlich einen gewaltigen Unterschied, ob z.B. eine (einzige) Kakaopackung

• 5 Cent (spottbillig!) oder aber
• fünf 500-Euro-Scheine, also insgesamt 2500 Euro (geradezu absurde Halsabschneiderei!)

kostet

(mal ganz abgesehen von der Größe der Packungen).

Wenn man derart rabiat alles Unmathematische wegamputiert, bleiben von der Aufgabe

"Erna kauft eine Packung Kakao und zwei Packungen Kaffee für insgesamt 17 €.
Karl kauft drei Packungen Kakao und vier Packungen Kaffee für insgesamt 39 €.
Wieviel kostet eine Packung Kakao und wieviel kostet eine Packung Kaffee?"

nur noch die bunt markierten Informationen über und ergibt sich somit das Gleichungssystem

1•x + 2•y = 17
3•x + 4•y = 39.

• Stark abgekürzt zum Stockwerkbeispiel: auch hier sind nur die farbig markierten Details in

"Ein Stockwerkmodul A und zwei Stockwerkmodule B sind insgesamt 17 m hoch.
Drei Stockwerkmodule A und vier Stockwerkmodul B sind insgesamt 39 m hoch.
Wie hoch ist ein Stockwerkmodul A und wie hoch ist ein Stockwerkmodul B?"

mathematisch relevant, die kurz

1•x + 2•y = 17
3•x + 4•y = 39

ergeben.

Schon gar nichts aber haben

• einerseits Kakao-/Kaffee-Packungen (Preise)
• andererseits Stockwerke (Höhen)

gemeinsam - außer den Zahlen und ihren Kombinationen zu Gleichungen.

(Daran kann man erkennen, warum die Mathematik überhaupt anwendbar ist: sie fragt eben nur nach Zahlen, und wen wundert es da, dass sie auch als Antwort nur Zahlen erhält?!:

• "Wie man in den Wald [mathematisch] herein ruft, so schallt es [mathematisch] heraus."
• "Wenn man ein Hammer [Mathematik] ist, scheint die ganze Welt aus Nägeln [Zahlen] zu bestehen.")

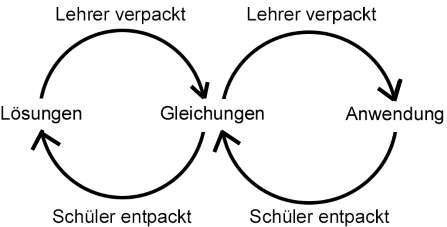
Beim Verpacken mathematischer Gleichungen in "Anwendungen" sind wir also so vorgegangen:

Ingesamt sind sieht der Verlauf also so aus:

Wie lächerlich die meisten "Anwendungs"-Verpackungen in der Schulmathematik sind, wird schön an dem Beispiel

(Screenshot aus dem Video ;
keine Ahnung, was das "für sich" soll)

deutlich

(von dem ich die Stockwerksidee geklaut habe):

es ist allerdings eine offensichtlich absichtliche Lächerlichkeit, denn mit dem Khan-Hauptquartier und der Mathechaussee wird ja deutlich signalisiert, dass die ganze Situation rein fiktiv, also keine echte Anwendung ist.

Und offensichtlich absichlich lächerlich sind auch die eingebauten unwichtigen Informationen wie etwa die Hausnummer oder die Parkplatzgröße.

(Nebenbei: merkwürdig, dass man mit Hausnummern überhaupt nicht sinnvoll rechnen kann!)

Das erinnert doch sehr an

"Weil du gerade Geometrie und Trigonometrie machst, will ich dir eine Aufgabe geben: Auf dem Meer ist ein Schiff, es kommt von Boston, es ist beladen mit Indigo, es hat zweihundert Registertonnen und segelt nach Le Havre, der Großmast ist zerbrochen, auf der Back befindet sich ein Schiffsjunge, Passagiere gibt es insgesamt zwölf, der Wind steht Ostnordost, die Schiffsuhr zeigt nachmittags Viertel nach drei, und es ist Mai ... Wie alt ist der Kapitän?"
(Gustave Flaubert),

wobei Flaubert doch nur ironisch ein Gefühl auf den Punkt gebracht hat, das viele Schüler mit Recht bei den allermeisten verpackten Mathematikaufgaben haben.

Und doch ist die Aufgabe

sinnvoll:

• normalerweise enthalten verpackte Matheaufgaben genau diejenigen mathematischen Informationen, die zur Lösung der Aufgabe nötig sind, aber keine überflüssigen mathematischen Informationen, aber auch nicht zu wenig mathematische Informationen (so dass die Aufgaben gar nicht lösbar wären);
• mit der Aufgabe

sollen die Schüler nun aber lernen, jene durchaus auch mathematischen Informationen auszusortieren, die für die Lösung der Aufgabe dennoch überflüssig sind, d.h. die Schüler erhalten keine vorgefilterte "Welt", sondern müssen aus dieser überhaupt erst selbst die (relevante) Mathematik herausfiltern. Genau das macht aber doch die meisten echten Anwendungsaufgaben aus: es ist vorweg noch gar nicht klar,

• was an ihnen mathematisierbar ist,
• welche der zahlreichen mathematischen Informationen für eine bestimmte Fragestellung relevant sind,
• welche vielleicht durchaus relevanten mathematischen Informationen zwecks einfacherer Rechnung vernachlässigt werden können,
• mit welchen mathematischen Mitteln die Aufgaben

(wenn überhaupt)

lösbar sind

(während im üblichen Mathrmatikunterricht die Anwendungsaufgaben immer garantiert mit genau jenen mathematischen Mitteln lösbar sind, die gerade im Unterricht durchgenommen wurden),

• ob die nötigen mathematischen Mittel überhaupt schon zur Verfügung stehen.

(Nebenbei: das eben gezeigte Stockwerk-Video stammt aus dem Lernvideo-Fundus der . Der deutsche National-Philosoph Precht hat diese Lernvideos in seinem Buch über die Schulmisere hochgelobt, und überhaupt sind diese Videos international vielfach ausgezeichnet worden. Ich hingegen finde sie lieblos zusammengestoppelt, also drittklassig.)

Bei den Pseudo-Anwendungsaufgaben ist meistens die Fragestellung "falschrum". Nehmen wir als Beispiel nur nochmal die Stockwerk-Aufgabe:

• üblicherweise sind vorher

• die Höhe eines Moduls A (5 m) und
• die Höhe eines Moduls B (6 m)
  

bekannt und fragt man sich dann z.B., wie hoch

• ein Modul A und
• zwei Module B

zusammen sind,

• niemand möchte aber umgekehrt wissen,
  • wie hoch
    • ein Modul A und
    • ein Modul B sind,
  • wenn
    • ein Modul A und zwei Module B insgesamt 17 m hoch sind,
    • drei Module A und vier Module B insgesamt 39 m hoch sind.
      

Das hieße doch, aus zwei Hochhäusern

(z.B. einem in Dubai, dem anderen in Buxtehude)

auf die Höhe der beiden Module schließen zu wollen. Da misst man doch lieber an dem einen Hochhaus in Buxtehude die Höhe der beiden Module A und B nach - und spare sich den Flug nach Dubai.

Die eingekleideten Pseudo-Anwendungsaufgaben sind meist derart lächerlich, dass ich in einer Klasse schonmal einen Preis für die bescheuertste Verpackung ausgeschrieben habe

(Standardgewinn ist bei mir immer ).

Statt die Schüler mit derart lächerlichen Pseudo-Anwendungsaufgaben zu verarschen, wäre es oft ehrlicher, sie einfach wegzulassen - und reine Mathematik zu treiben.

Nebenbei: Christos Reichstagsverpackung war natürlich keine Kunst, sondern nur gefällig (hübsch).

Zurück zum Titel "Mathematik hübsch verpacken": da hinkt der Vergleich mit Christos Reichstagsverpackung, weil bei dieser jeder vorweg wusste, was da verpackt wurde

(und man es auch an den Konturen der Verpackung erkennen konnte).

Ein im Hinblick auf die Mathematik schon treffenderes Bild ist da : da weiß zwar jeder grob, was drin ist, nämlich Mathematik, aber noch nicht die Details (Lösungen).

Allerdings ist pure Ironie, denn der mathematisch Inhalt der Geschenkverpackung ist den meisten Schüler ja nicht gerade willkommen, das Geschenk also eher bösartig. Und genauso ist auch das Wort "hübsch" Ironie, denn was z.B. an der Verpackung

"Erna kauft eine Packung Kakao und zwei Packungen Kaffee für insgesamt 17 €.
Karl kauft drei Packungen Kakao und vier Packungen Kaffee für insgesamt 39 €.
Wieviel kostet eine Packung Kakao und wieviel kostet eine Packung Kaffee?"

ist hübsch?!