Weg, Geschwindigkeit, Beschleunigung
oder
die
physikalischen Bedeutungen der Ableitungen
![]() die physikalische
Vorgeschichte
die physikalische
Vorgeschichte
![]() Vorkommen in der
Schulmathematik
Vorkommen in der
Schulmathematik
die physikalische Vorgeschichte
Es gibt in Textaufgaben erstaunlich wenige Anwendungsmöglichkeiten der Ableitungen. Eine der wenigen, die häufig vorkommt, ist da
 :
:
als laut einer
Anekdote Isaac Newton
 mal unter einem
Apfelbaum saß und sich ein Apfel löste, der ihm glücklicherweise
exakt auf seine geniale
Perücke fiel, soll Newton die entscheidende Erkenntnis über den freien Fall
gekommen sein:
mal unter einem
Apfelbaum saß und sich ein Apfel löste, der ihm glücklicherweise
exakt auf seine geniale
Perücke fiel, soll Newton die entscheidende Erkenntnis über den freien Fall
gekommen sein:
s =![]() •
g • t2
•
g • t2
![]()
In dieser Gleichung ist
(den der Apfel zurückgelegt hat, seit er sich vom Baum gelöst hat),
(die Gravitationskonstante ist überall auf der Erde annähernd gleich; auf anderen Himmelskörpern hat sie hingegen andere Werte: ),
(seit der Apfel sich vom Baum gelöst hat).
Da ![]() und
g Konstanten sind, ist an der Gleichung
s =
und
g Konstanten sind, ist an der Gleichung
s =![]() •
g • t2
erstmal nur s =
xxx t2
interessant:
•
g • t2
erstmal nur s =
xxx t2
interessant:
Der Weg s ist also
(z.B. s
=![]() •
g • t
, also ohne 2 ),
•
g • t
, also ohne 2 ),
Nochmal kurz zu a.: eine lineare Abhängigkeit zwischen dem Weg s und der Zeit t würde bedeuten, dass
Das aber würde bedeuten, dass der Apfel
(Nebenbei: ein bisschen merkwürdig scheint mir das ja doch zu sein: wie erreicht der Apfel dann denn gleich zu Anfang seines Falls die danach immer gleichbleibende Geschwindigkeit? Er müsste zumindest am Anfang eben doch urplötzlich auf diese Geschwindigkeit beschleunigen!?
Mich erinnert das an die Theorie von der anfänglichen Inflation des Universums:
"Als kosmologische Inflation wird
eine Phase extrem rascher Expansion des Universums bezeichnet, von der man
annimmt, dass sie unmittelbar nach dem Urknall stattgefunden hat."
[Quelle:
![]() ])
])
|
Es ist so leicht und billig, sich im Nachhinein über die Menschen lustig zu machen, die jahrhundertelang (spätestens seit Aristoteles
geglaubt haben, Gegenstände würden gleichmäßig immer mit derselben Geschwindigkeit fallen: es gab ja kaum Möglichkeiten, das zu überprüfen, denn beim Fall von den höchsten Gebäuden der damaligen Zeit und bei den damaligen Möglichkeiten der Zeitmessung waren exakte Messungen kaum möglich (s.u. bei Galilei). Ansonsten siehe |
|
|
|
Seit Newton wissen wir aber, dass ein fallender Gegenstand immer schneller fällt, weil er permanent beschleunigt wird
(und überhaupt hat Newton sich vor
allem um beschleunigte Bewegungen gekümmert; ein nicht
beschleunigter oder gebremster Gegenstand ist langweilig: er fliegt in alle
Ewigkeit immer
gleichschnell geradeaus [Trägheit]).
Die permanente Beschleunigung hat zur Folge, dass fallende Gegenstände enorm schnell und deshalb auch gefährlich werden, weshalb auf hohen Türmen oftmals Schilder stehen, auf denen das Herabwerfen von (scheinbar harmlos leichten) Gegenständen verboten wird:


Grund für permanente Beschleunigung eines fallenden Körpers ist die Erdanziehung (Gravitation), die
(und das ist wohl eine der wichtigsten Erkenntnisse Newtons)
permanent und
(wie wir noch sehen werden)
gleichmäßig, also nicht kompliziert quadratisch, sondern ganz einfach konstant auf einen fallenden Körper einwirkt.
(Ich vermute sogar, dass Newton mit dieser konstanten Erdanziehung angefangen und daraus „rückwärts“
[durch zweimaliges „Aufleiten“ bzw. doppelte Integration]
die Geschwindigkeit und den Weg berechnet hat, wozu
er „eben mal kurz“ nicht nur das mathematische Mittel der Ableitung, sondern
auch die Integration entwickeln musste. Und deshalb ist er nicht nur in die
Geschichte der Physik, sondern auch in die Geschichte der Mathematik als eines
der größten Genies aller Zeiten eingegangen:
 .
.
Vgl. allerdings auch  .)
.)
Allemal irritierend an der Gleichung s =![]() •
g • t2
ist aber, was nicht in ihr vorkommt, nämlich die
Masse m (das Gewicht) des fallenden Körpers. Das aber bedeutet, dass der
zurückgelegte Weg s
•
g • t2
ist aber, was nicht in ihr vorkommt, nämlich die
Masse m (das Gewicht) des fallenden Körpers. Das aber bedeutet, dass der
zurückgelegte Weg s
was wiederum bedeutet:
(was
allerdings schon seit Galilei
 bekannt war).
bekannt war).
Das aber widerspricht doch aller direkten Anschauung:
beispielsweise eine und
ein
und
ein fallen
fallen
(wenn man sie aus gleicher Höhe fallen lässt)
offensichtlich nicht mit derselben Geschwindigkeit zu Boden, sondern der Hammer ist viel früher unten als die Feder, was u.a. daran liegt, dass
(also einen viel längeren Weg zurücklegt):
Wenn man nun vermutet,
liegt man schon halbwegs richtig: fallen Feder und Hammer denn gleich schnell, wenn man die Luft weglässt, beide also in einem Vakuum fallen
(was eine enorme Abstraktion ist, da es einen komplett luftleeren Raum nirgends auf der Erde gibt, und zwar selbst dann nicht, wenn man die Luft mit stärksten Pumpen abpumpt)?
Bzw. ist die Luft überhaupt das entscheidende Problem?: würden eine leichte Feder und ein schwerer Hammer denn wenigstens im Vakuum gleich schnell fallen?
Ab und zu lohnt es sich, in Extremen zu denken, weil dann eher offenbar wird, was im Kleinen
(bei fast gleich schweren Gegenständen)
kaum deutlich wird:
(oder eine Mücke
![]() )
)
 [stark verkleinert]
[stark verkleinert](oder einen echten Elefanten
 [stark verkleinert];
[stark verkleinert];
keine Bange, wir werfen nicht echte Tiere von einem Hochhaus herunter ).
Da scheint es doch höchst unglaubwürdig, dass
gleichzeitig den Erdboden erreichen
(und zwar selbst dann, wenn wir die armen Tiere im [tödlichen] Vakuum fallen lassen würden).
Und doch ist es so, wie zwei Experimente beweisen:
(Wo ich schon dabei bin, hier noch ein nettes Schmankerl: )
Aber zu beiden soeben gezeigten Freier-Fall-Experimenten bedarf es enormer
moderner Technik, die Galilei noch gar nicht zur Verfügung stand. Wie ist er
dennoch „drauf“ gekommen? Denn die Anekdote, er habe Gegenstände vom Schiefen
Turm von Pisa geworfen  , erscheint doch zweifelhaft: der Turm ist überhaupt nicht
hoch genug, denn ein herabgeworfener Gegenstand ist viel zu schnell unten, als
dass mit damaligen Mitteln halbwegs exakte Beobachtungen möglich gewesen wären
(vgl.
, erscheint doch zweifelhaft: der Turm ist überhaupt nicht
hoch genug, denn ein herabgeworfener Gegenstand ist viel zu schnell unten, als
dass mit damaligen Mitteln halbwegs exakte Beobachtungen möglich gewesen wären
(vgl.
![]() ).
).
Vermutlich ist es so gelaufen:
(u.a. der, dass ein fallender Körper immer gleich schnell falle und die Fallzeit abhängig von seinem Gewicht sei),
so dass er (Galilei) überhaupt erst die Notwendigkeit einer Überprüfung sah,
„ • Angenommen man hat einen leichten und einen schweren Körper.
Was würde passieren, wenn man sie [...] miteinander verbindet [z.B. eine kleine und eine große Eisenkugel aneinanderschweißt]? Es gibt zwei Möglichkeiten, die beide logisch sind, sich aber widersprechen:
Die Lösung aus diesem Dilemma kann nur in der
Annahme bestehen, dass [die Annahme, „dass der schwere Körper schneller fällt
als der leichte“, falsch war, dass also] alle Körper gleich schnell fallen.“
(Quelle:
![]() ; nebenbei: Galileis
Gedankengang funktioniert genauso wie der „Widerspruchsbeweis“ in der
Mathematik.)
; nebenbei: Galileis
Gedankengang funktioniert genauso wie der „Widerspruchsbeweis“ in der
Mathematik.)
Es scheint aber erst Newton gewesen zu sein, der Galileis Erkenntnisse in die
mathematische Form
s =![]() •
g • t2
bringen konnte.
•
g • t2
bringen konnte.
Mit dieser Gleichung wurden erstmals (nichtlineare) natürliche Vorgänge mathematisierbar - und begann der Siegeszug der Mathematik in den Naturwissenschaften
(was ein Grund dafür ist, dass Newtons Mathematik [Ableitung und Integration] bis heute Standardthemen der Schulmathematik sind).
Die Gleichung
s =![]() •
g • t2
ist also derart bedeutsam, dass sie eigentlich umgehend in die
•
g • t2
ist also derart bedeutsam, dass sie eigentlich umgehend in die
![]() „Repräsentative Liste des
immateriellen Kulturerbes der Menschheit“
„Repräsentative Liste des
immateriellen Kulturerbes der Menschheit“
 aufgenommen werden
müsste!
aufgenommen werden
müsste!

Dass der Weg s in der Gleichung
s =![]() •
g • t2
in Abhängigkeit von der
Zeit t dargestellt ist, kann man auch verdeutlichen, indem man schreibt:
•
g • t2
in Abhängigkeit von der
Zeit t dargestellt ist, kann man auch verdeutlichen, indem man schreibt:
s
( t ) =![]() •
g • t2
•
g • t2
Z.B. ergibt sich für die Fallzeit t = 1 sec der Fallweg
s
( 1 sec) =![]() •
g •
(1 sec)2 ≈
•
g •
(1 sec)2 ≈
. ≈ ![]() •
9,81
•
9,81
![]() •
sec 2
=
•
sec 2
=
= ![]() •
9,81 m
=
•
9,81 m
=
= 4,905 m ≈ 5 m ,
d.h. nach einer Sekunde ist der Gegenstand ca. 5 m weit gefallen.
Newton konnte aber nicht nur den Fallweg, sondern auch die Fallgeschwindigkeit und die Beschleunigung berechnen:
v
(
t
) =
s
'
(
t ) = g • t
![]()
(woran bemerkenswert ist, dass die Fallgeschwindigkeit v
Weshalb das so ist, sei erstmal an einem einfachen Beispiel gezeigt:
der Fallweg s nehme probehalber doch mal linear und nicht quadratisch zu:

Nun ist die
Geschwindigkeit v bekanntermaßen der Bruch aus der
Strecke s und der Zeit t, also z.B.
v (t)
= ![]() = 100
= 100
![]()
 .
.
Geometrisch lässt sich die Geschwindigkeit v durch ein Steigungsdreieck erfassen
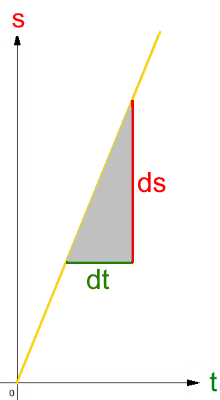
Die
Geschwindigkeit v / Steigung lässt sich dann errechnen als
v (t)
= ![]() .
.
Weil die Wegfunktion linear ist, ist es dabei egal, wo man das Steigungsdreieck hinzeichnet und wie groß man es zeichnet: es kommt immer dieselbe Geschwindigkeit v / Steigung heraus, d.h. z.B., dass das Auto immer gleich schnell ist.
Nun aber wieder zu einer quadratischen (gekrümmten) Zeit-/Weg-Funktion:

Hier lassen sich nun nicht mehr
in allen Punkten des Graphen
Steigungsdreiecke mit demselben
Seitenverhältnis
![]() zeichnen
zeichnen
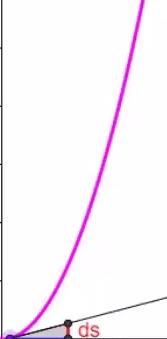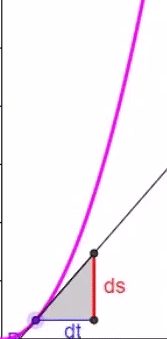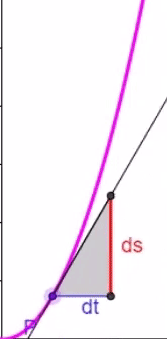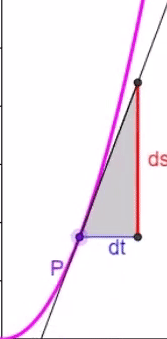 ,
,
sondern die je nach Punkt P unterschiedliche Steigung / Momentan[!]-Geschwindigkeit v (t) lässt sich nur durch die Ableitung s ' ( t ) bestimmen:
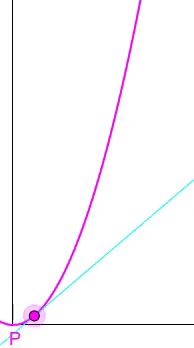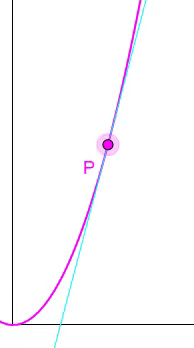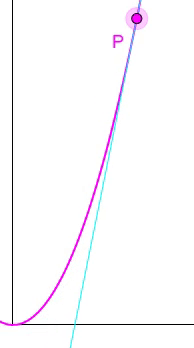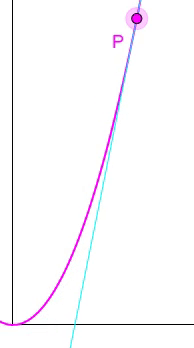
a
(
t
) =
v
'
(
t
)
=
s
' '
(
t ) = g
![]()
(woran bemerkenswert ist, dass die
Beschleunigung a konstant ist,
nämlich g
≈ 9,81
![]() :
:
Zur Vereinfachung runden wir
g ≈
9,81
![]() ≈
10
≈
10
![]() .
.
Zudem lassen wir als echte Mathematiker mal dreist die Einheiten weg und ersetzen zudem das Ungefährzeichen ≈ durch ein Gleichheitszeichen, womit sich ergibt:
g = 10
Daraus folgt:
s
( t
) = 5 t2
![]() ,
,
für die Fallgeschwindigkeit v ( t ) = s ' ( t ) = g • t = 10 t bzw. kurz
v (
t )
= s
'
(
t ) =
10 t
![]() ,
,
für die Beschleunigung
a (
t )
= s
' '
(
t ) =
10
![]() .
.
Vorkommen in der Schulmathematik
Wenn wir die physikalische Schreibweise nun in die übliche mathematische Schreibweise übersetzen, ergibt sich
|
Diese Vorgehensweise funktioniert aber nicht nur für den freien Fall, also die Funktion f : y) = 5 x2 , sondern für jede differenzierbare, also ableitbare Funktion f , also z.B. auch
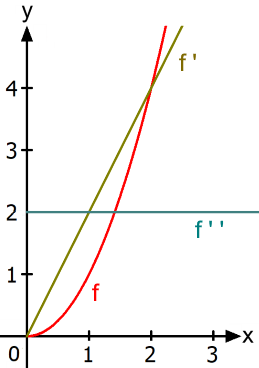
Weil im Funktionsterm x2 von f nicht mehr die 5 vorkommt, liegt hier auch nicht mehr der freie Fall vor
(oder zumindest nicht der auf der Erde),
sondern eine andere Bewegung
(bzw. Entwicklung; s.u.),
nämlich z.B. der von einem Auto zurückgelegte Weg.
Wie immer, so benötigt man auch hier die Ableitungen f ' und f ' ' nur, um mittels dieser beiden Ableitungen Aussagen über die Ausgangsfunktion f machen zu können. Wir gehen hier mal umgekehrt vor, arbeiten uns also von f ' ' über f ' zu f hoch:
Nun muss die Ausgangsfunktion f nicht unbedingt im wörtlichen Sinn einen Weg beschreiben, bzw. letztlich lässt sich jede Zahl als Weg verstehen, nämlich z.B.

als
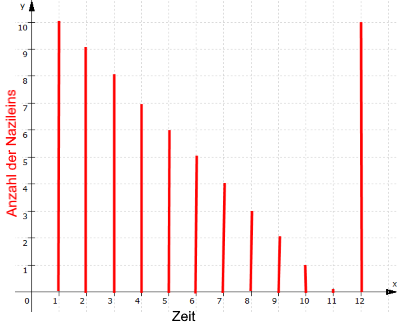 .
.
Und so kann die Ausgangsfunktion f z.B. auch von der Entwicklung der Erdbevölkerung im Laufe der letzten 2000 Jahre handeln:
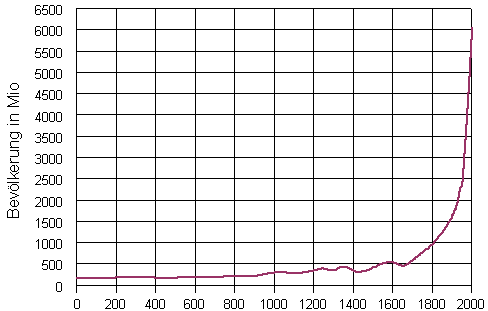
(... wobei die Dellen die Pestzeit und den Dreißigjährigen Krieg anzeigen.)
Probehalber sei dieser Funktionsgraph mal durch die Funktion f: y = e (x-18,3) + 0,1 angenähert:
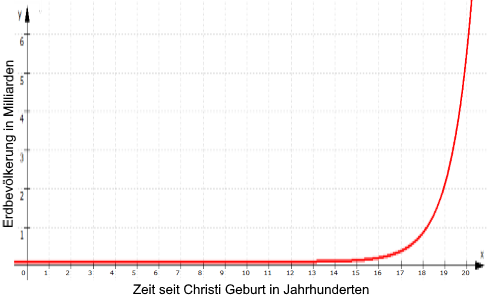
Mit f: y = e (x-18,3) + 0,1 errechnet sich
die Geschwindigkeit der Menschheitsvermehrung als f ' : y = e (x-18,3) ,
die Beschleunigung der Menschheitsvermehrung als f ' ' : y = e (x-18,3) .
Die Funktionsgraphen der Geschwindigkeit und der Beschleunigung sehen also fast genauso aus wie der Funktionsgraph der Ausgangsfunktion f.
Und das ist nun wirklich fatal, bedeutet es doch, dass die Beschleunigung und die Geschwindigkeit der Menschheitsvermehrung immer rasanter wachsen - und damit explodiert erst recht die Anzahl der Menschen auf der Erde:
Aber es gibt doch einen (scheinbaren?) Anlass für Optimismus:
Dabei
ist "langsamer" allerdings (leider) keine Aussage über die Anzahl der Menschen auf der Erde
(die weiterhin zunehmen kann, wenn auch nicht mehr so schnell wie bisher),
sondern "langsamer" besagt nur, dass die Geschwindigkeit der Menschheitsvermehrung abnimmt, also fällt.
Ein Hoffnungsschimmer ist schon eher:
"Die Zeit des endlosen Wachstums ist vorbei" ist nämlich endlich mal eine Aussage direkt über die Anzahl der Menschen auf der Erde, also die Ausgangsfunktion f.
Allerdings ist "Die Zeit des endlosen Wachstums ist vorbei" auch nur bedingt richtig:
ist hier nur von einer Hochrechnung die Rede, die sich in der Zukunft auch als falsch erweisen kann,
wächst die Anzahl der Menschen auf der Erde laut der Hochrechnung durchaus noch bis 2064 weiter
(wenn auch nicht mehr so schnell wie bisher)
- und verringert sie sich vermutlich erst danach:

Um das Bisherige mit
![]() auszudrücken:
auszudrücken:
wenn die "Weg-Funktion" f als Ausgangsfunktion gegeben ist, gilt
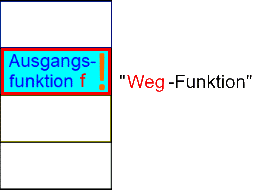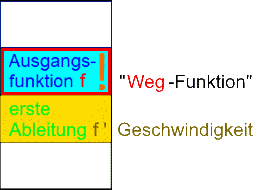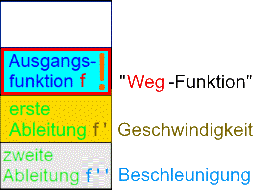
Manchmal geben Lehrern aber aus purem Übermut die Geschwindigkeitsfunktion als Ausgangsfunktion f . Dann rutschen alle Funktionen eine Zeile weiter nach oben und ist die "Weg-Funktion" mittels Stammfunktion zu ermitteln:

Also  , wenn die Funktion, deren Funktionsgleichung vorgegeben ist, mit "Geschwindigkeit"
markiert ist.
, wenn die Funktion, deren Funktionsgleichung vorgegeben ist, mit "Geschwindigkeit"
markiert ist.
Ein Beispiel (ohne weitere Erklärungen):
