wenn (H)einer eine Reise tut ...

Man muss sich noch (über Unscheinbares) wundern können.

Heutzutage gibt es ja angeblich keine wirklichen Entdeckungsreisen und Abenteuer mehr

(irgendwo habe ich mal gelesen, das letzte Abenteuer sei Vaterschaft - ganz schön bitter!),

weil überall, wo man hinkommt, schon McDonalds oder zumindest Studiosus "Ich bin schon da!" schreien.

Bzw. wenn's hoch kommt, entdeckt man in einer fremden Kultur vor allem

(weil man das größte Problem, nämlich sich selbst, immer mit nimmt)

sich selbst bzw. das Fremde in sich.

Ach was, alles Blödsinn: es gibt noch immer genug unberührte Flecken in der Welt - und fremdartige Kulturen

(wozu man gar nicht in den Regenwald am Amazonas fahren muss, sondern schon die kleinen Eigenarten beispielsweise der Holländer sind faszinierend-irritierend genug).

Meine Reiseabenteuer sind kleiner - und dennoch auch eindrücklich:

Im November 2006 war ich auf Norderney -  und noch faszinierender als alles im Folgenden Dargestellte waren allemal

1. die sturmgepeitschte Nordsee ("ich und die Elemente"),

2. das Zusammensein mit meinem besten Freund und zwei Kindern (seinem, meinem).

Als ich ins Hotelzimmer kam und dann mal "für kleine Kängurus musste", passierte mir "hinterher" beim Badezimmerspiegel überm Waschbecken etwas durchaus Irritierendes:

egal, wie ich mich bewegte (an dem Spiegel vorbei ging), ich sah mich selbst immer an derselben Stelle

(hier nachgestellt mit Kamera - weshalb ich auch so blöd in diese schiele):

(Nebenbei: in einem normalen Einfachspiegel - und an den hat man sich ja vor allem gewöhnt - bleibt das Spiegelbild, wenn man sich am Spiegel vorbei bewegt, nicht an einer Stelle stehen, sondern wandert mit einem mit.)

Nun ist der faszinierende Effekt hier mit Fotos leider kaum wiedergebbar: weil ich mit der Kamera immer auf mein feststehendes Spiegelbild gezielt habe (es immer etwa in der Mitte der Fotos ist), kann man meine Bewegung nur indirekt daraus erschließen, dass sich der Hintergrund verschiebt:

Einige werden den Grund für den Effekt vielleicht schon erahnt haben

(woher kommt der senkrechte Strich mitten "durch" mich?),

bei mir stellte sich die Erkenntnis allerdings erst nach einer "Schreck-" bzw. Staun-Sekunde ein:

in dem Badezimmer waren zwei Spiegel senkrecht zueinander montiert:

(Ansicht von oben)

Der Effekt, dass das eigene Spiegelbild bei senkrecht zueinander stehenden Spiegeln immer bewegungslos an der Schnittlinie der beiden Spiegel verbleibt, obwohl man sich selbst bewegt, ist mir natürlich nicht neu - und fasziniert mich doch immer wieder.

Auf die Schnelle hatte ich da immer die Kurzerklärung "das Licht fällt halt irgendwie immer genauso ein, wie es auch wieder ausfällt".

Jetzt aber will ich es endlich genauer wissen ("irgendwie" reicht mir nicht mehr).

Nun habe ich da natürlich meine Hilfsmittel:

1. weiß ich noch aus dem Physikunterricht in der Schule, dass bei Spiegeln "Einfallswinkel = Ausfallswinkel" gilt.

2. bin ich Mathematiker genug, um zu wissen, dass eine Untersuchung nur dann für alle Bewegungspunkte gilt, wenn ich keine konkreten Positionen und Winkel benutze

(man beachte: in der folgenden Planskizze ist das natürlich unvermeidbar, aber in der Argumentation taucht [außer dem rechten Winkel zwischen den beiden Spiegeln] nie ein konkreter Winkel auf).

Der Einfachheit halber sei vorerst nur der "Sehstrahl" eines Auges betrachtet, wobei der Kopf (anfangs) bewusst in einer beliebigen Position ist und das Auge in (fast) beliebige Richtung schaut

("fast", denn immerhin muss der Sehstrahl zur Erklärung des Effekts beide Spiegel "treffen"):

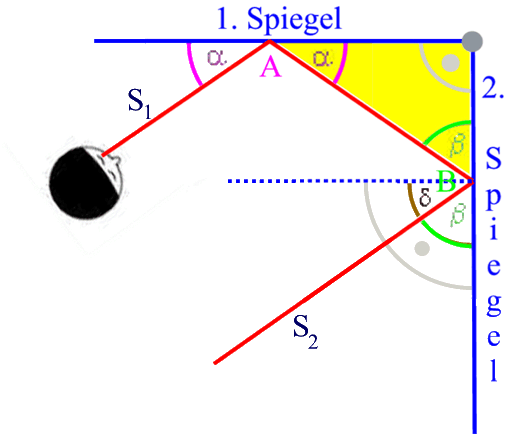
Schauen wir uns nun im Einzelnen an, was da nacheinander passiert:

1. beim Punkt A: der Sehstrahl fällt im selben Winkel α ein, wie er ausfällt.

2. im gelb unterlegten Dreieck: da in jedem Dreieck die Winkelsumme 180⁰ ist und das gelb unterlegte Dreieck zudem (rechts oben) rechtwinklig ist, gilt

180⁰ = α + β + 90⁰

bzw.

β  =  90⁰ - α  *

3. beim Punkt B, durch den punktiert ...... eine Parallele zum ersten Spiegel gezogen wurde:

90⁰ =      β          + δ

Wenn wir nun darin das Ergebnis aus * einsetzen, ergibt sich

90⁰ =    90⁰ - α   + δ

und daraus sofort:

δ = a

Damit ist immerhin geklärt, dass die beiden Strahlen S₁ und S₂ parallel zueinander laufen.

In der Planskizze tritt allerdings noch ein kleines "Missgeschick" ein, denn die Figur schaut seitlich an sich selbst vorbei, sieht sich also gar nicht selbst im Doppelspiegel. Nun sollte einen das allerdings nicht allzu sehr wundern, denn auch bei einem normalen Einfachspiegel sieht man sich ja nicht selbst, wenn man schräg in den Spiegel schaut. Vielleicht einfach, weil der Zweck eines Spiegels gerade darin besteht, sich selbst zu sehen

("ich kenn' dich nicht, aber ich wasch' dich trotzdem"),

sucht man sich wohl schnell selbst im Spiegel und schaut schnell dorthin, wo man zu sehen ist.

Aber wohin muss man denn sehen, um sich bei einem Doppelspiegel zu sehen?: in die Ecke, wo sich beide Spiegel rechtwinklig treffen - woraufhin man einwenden könnte (müsste), dass wir damit voraussetzen, was eigentlich erst zu beweisen wäre.

Schauen wir uns aber einmal an, was passiert, wenn man tatsächlich in die Ecke schaut ........... , wo sich die beiden Spiegel treffen:

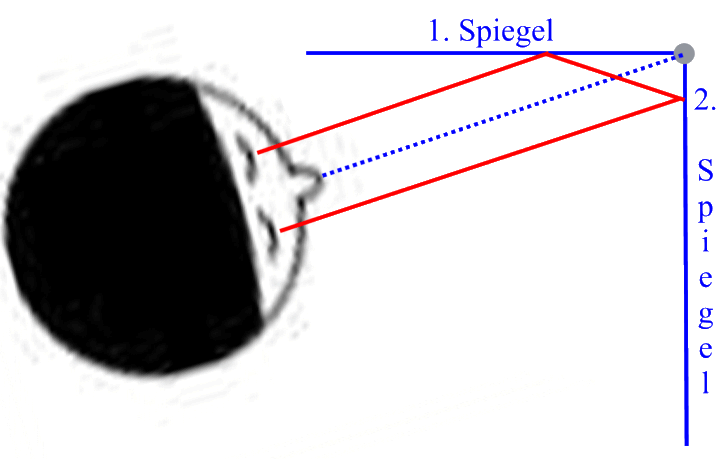
Alle Winkel-Argumente der vorherigen Planskizze bleiben hier natürlich erhalten, so dass schon mal klar ist, dass die beiden "Augenstrahlen" wieder parallel sind.

Rein konstruktiv (nach der Einheitsregel "Einfalls- = Ausfallswinkel") ergibt sich aber zudem augenscheinlich (noch nicht bewiesen!), dass die beiden "Augenstrahlen" zusätzlich auch gleich weit von der Sehrichtung......... entfernt sind, dass also

• der Strahl vom rechten in das linke Auge und

• der Strahl vom linken in das rechte Auge fällt.

Oder anders gesagt:

• das rechte Auge sieht im rechten Spiegel das linke Auge,

• das linke Auge sieht im oberen Spiegel das rechte Auge.

Den Beweis, dass das tatsächlich so ist, will ich hier (auch aus Zeitgründen) nicht in allen Details ausführen.

(Nur so viel: am Treffpunkt der beiden Spiegel ließe sich - unter Zuhilfenahme der Winkelargumentation weiter oben - mit kongruenten Dreiecken argumentieren:

).

Wichtig ist vor allem, dass (wie oben gefordert) nie genau festgelegt wurde, wo der Kopf sich befindet, so dass die gesamte Argumentation für jede Position des Kopfes bzgl. der Spiegel gilt.

(Nebenbei: mit dem Strahlengang in der vorletzten Zeichnung könnte man auch erklären, warum man sich im Doppelspiegel "richtig rum", d.h. nicht spiegelverkehrt sieht; s.u.)

Der scheinbar so einfache Sachverhalt

(dass man sich trotz Bewegung immer fest in der Spiegelecke sieht)

ist also keineswegs so einfach zu beweisen. Kommt hinzu, dass die mathematisch-physikalische Erklärung völlig abstrakt (vielfach um die Ecke gedacht bzw. "gespiegelt"), also uneinholbar weit vom Effekt entfernt ist: das pure Staunen über den Effekt bleibt.

Immerhin beweist die mathematisch-physikalische Erklärung, dass auch der Effekt keineswegs so selbstverständlich bzw. banal ist - mich also mit gutem Grund irritiert hat.

Nicht umsonst habe ich auf den Fotos den erstbesten Text (die "Brandschutzordnung" des Hotels) vor mich gehalten:

• bei einem Foto in einen Spiegel erscheint die Schrift natürlich spiegelverkehrt:

• beim Foto in beide Spiegel findet aber eine Doppelspiegelung statt, ist die Schrift also nicht spiegelverkehrt, sondern normal lesbar:

Im Doppelspiegel sieht man sich also (endlich mal) so, wie andere einen sehen.

Dass die Schrift im Doppelspiegel "richtig rum" erscheint, scheint ein Anzeichen dafür zu sein, dass der Doppelspiegel alles viel einfacher macht. Aber weit gefehlt:  man fasse sich z.B. mal vor solch einem Doppelspiegel mit der rechten Hand ans rechte Ohr. Dann fasst sich das Spiegelbild - und das ist völlig irritierend - mit der linken Hand ans linke Ohr.

Ich habe mal versucht, mich vor diesem Doppelspiegel zu rasieren - was zu einer permanenten Irritation und falschen Handgriffen führte: die Hand gerät da in permanenten Widersprung zum Auge, d.h. man wird fast "schizophren".

Und noch etwas Merkwürdiges ist mir aufgefallen: auf den ersten Fotos meinerselbst im Doppelspiegel geht die Trennlinie nicht mitten durch mich durch, sondern

• im Spiegelbild durch mein rechtes Auge,

• im "Original" also durch mein linkes Auge:

Erst im Nachhinein fiel mir auf, woran das liegt: ich bin auf meinem rechten Auge fast blind, sehe also nur mit meinem linken Auge - und habe dementsprechend die Kamera gehalten.

Erst mit einigen Verrenkungen ist es mir dann gelungen, ein Foto zu machen, in dem die Trennlinie genau durch meine Mitte geht:

Erst im Nachhinein erfahre ich, dass Physiker Spiegelanordnung der genannten Art

(die es wohl auch dreidimensional, also mit drei rechtwinklig zueinander angeordneten Spiegeln gibt)

anscheinend "Reflektoren" nennen. Aber der Physiker, der mir das erzählte, konnte gar nicht mehr staunen und brachte (deshalb) auch nur die Banalerklärung, dass die Strahlen "irgendwie" genauso einfallen, wie sie ausfallen.

Sicherlich gab es auch schon vorher präzise Erklärungen des Effekts, aber es erfüllt mich doch mit Stolz, sie - aufgrund meines Staunens! - selbst gefunden zu haben.

Fragt sich nur, ob solche Spiegelfechtereien irgendjemanden außer mir, ob sie also beispielsweise auch SchülerInnen interessieren könnten.

Ein guter Maßstab dafür, was "den" Menschen, wenn er nicht schon völlig stumpf und fraglos (gemacht worden) ist, fasziniert, sind zweifelsohne kleine Kinder.

Und in einem später
en Urlaub gab's im Schlafzimmer einen Schrank, dessen Spiegeltüren man in beliebigem

(statt nur - wie oben - rechten)

Winkel gegeneinander klappen konnte, so dass man je nach Winkel verschieden viele Spiegelbilder seinerselbst sehen konnte. Und daran nun hatte mein vierjähriger Spross (von sich aus) einen Heidenspaß, ja, er spielte sogar mit seinen Spiegelbildern, dass sie (viele!) Freunde seien:

Vgl. auch .

Auf der Rückfahrt von Norderney stand ich auf dem Bahnhof von Norddeich-Mole und sah zufällig (auch nicht zum ersten Mal) Folgendes in einem Süßigkeitsautomaten:

Was man da in so einem popeligen Automaten sieht, sind hübsch hochtrabend gesagt "archimedische Schrauben".

In solche Schrauben sind die Süßigkeiten eingestellt, und wenn man nun den entsprechenden Knopf beispielsweise für "Lion" (fast genau in der Bildmitte) drückt, dreht sich die "Lion"-Spirale, bis das "Lion"-Päckchen vorne runter in einen Aufnahmebehälter fällt, aus dem man es dann entnehmen kann.

Ist das nicht genial bzw. genial einfach?!

Man kann an dem Foto auch erkennen, dass jeweils benachbarte Spiralen gegenläufig sind

(die eine ist [vom Betrachter aus] eine Links- und die andere eine Rechtsspirale - oder umgekehrt)

- was seinen guten Grund hat: größere Gegenstände wie z.B. Schokoladen werden zwischen zwei gegenläufige Spiralen geklemmt, und nur solche zwei gegenläufigen Spiralen haben an gleicher Position eine Einstecköffnung:

Damit das Ganze funktioniert, müssen sich die beiden gegenläufigen Spiralen natürlich auch gegenläufig drehen (im bzw. gegen den Uhrzeigersinn), was einen hübschen Symmetrieeffekt ergibt.