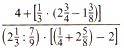
wie rechnet man das?: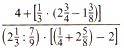

Dabei sei hier mal völlig dahingestellt, ob es überhaupt sinnvoll ist, sowas wie 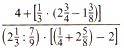rechnen zu können.

Keine Frage allerdings ist, dass sowas wie 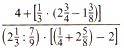nach wie vor oftmals im Unterricht durchgenommen und von SchülerInneN gefordert wird. Also kann es nicht schaden, Wege zur Entschlüsselung des (vielleicht überflüssigen) Problems zu zeigen.

Wenn überhaupt, so meine ich, dass die Fertigkeit, mit  - pars pro toto - 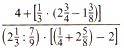umgehen zu können, auf andere Art sinnvoll ist, als es im üblichen Unterricht betrieben wird.

Man muss sowas wie 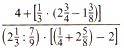nämlich nicht vollständig ausrechnen können (das mag zum Üben von Bruchrechenregeln ja sinnvoll sein, ist ansonsten aber doch eine Idiotentätigkeit), sondern sollte wissen, wie da "im Prinzip" vorzugehen wäre. ... und dementsprechend spare ich es mir hier auch, den vollständigen Lösungsweg vorzumachen (die vereinfachte Form von ist  - wie ich dem Lösungsheft entnehme - ).

Ein echtes Problem für viele SchülerInnen besteht nun darin, dass ihnen oftmals unklar ist, was nun eigentlich das Ziel des "Umgangs" mit 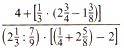ist. über dieser Aufgabe steht in dem Mathematikbuch, aus dem ich sie geklaut habe, ja nicht mal mehr eine Arbeitsanweisung.

Nun ist allerdings das Ziel oftmals als "Gewohnheitsrecht des Vorunterrichts" klar: 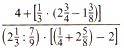soll "vereinfacht" werden

(was man davon "hat", ist dabei eine ganz andere Frage).

Oder anders gesagt: 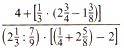ist eine höchst umständliche Schreibweise für eine exakt gleiche andere, und zwar viel einfachere Zahl (im vorliegenden Fall ).

(Merke: Zahlen können völlig unterschiedlich aussehen und doch exakt gleich sein. Zahlen "verkleiden" sich also sozusagen gern.

Die Urheber von  haben sich allerdings einen üblichen Gag vergeben, nämlich dass am Ende - oh Wunder über Wunder! - etwas vollständig Einfaches

[nämlich z.B. die natürliche Zahl 3 statt der doch schon relativ komplizierten gemischten Zahl ]

herauskommt.

[ist nun wahrhaft ein besonders hässliches Ergebnis, weil sich da kein Mensch etwas drunter vorstellen kann (soll?) - außer vielleicht

• auf den ersten Blick, dass es zwischen 1 und 2 liegt,

• auf den zweiten Blick, dass ≈ ]

Natürlich läuft das in Wirklichkeit andersrum: die Autoren probieren nicht zigtausend höchst komplizierte Brüche aus, bis irgendwann zufällig was Einfaches dabei heraus kommt [oder auch nicht], sondern sie gehen vom einfachen [und ihnen dann schon bekannten!] Ergebnis aus und "verkomplizieren" dann solange, bis die dummen SchülerInnen nicht mehr sehen, dass hinter eigentlich nur steckt.

Genau damit könnte man aber SchülerInnen vielleicht sogar "ködern": dass man ihnen dieses Rezept verrät und sie dann selbst vom einfachen Ergebnis aus schwierige Aufgaben entwickeln.)

Was also zu tun ist, ist im Grunde ganz einfach und fällt vielen SchülerInneN doch enorm schwer:

es ist eine Gleichungskette aufzustellen, in der von links nach rechts systematisch (!, s.u.) vereinfacht wird, also

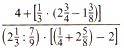= schon ein bisschen einfacher = noch einfacher = ... = ganz einfach

Wichtig dabei ist, dass zwischen den Einzelelementen wirklich immer Gleichheitszeichen stehen, man sich also kein einziges Mal verrechnet hat. Nur so sind das erste (schwierige) und das letzte (einfaches) Element wirklich gleich (und kann man dann später ruhig alle Zwischenelemente vergessen).

Wenn aber nur ein einziger Rechenfehler auftritt, also ein einziges Mal kein Gleichheitszeichen stehen darf

(was man allerdings oftmals leider nicht bemerkt),

zerbricht die ganze Gleichungskette, sind also

(es sei denn, man macht später andere Fehler, die zufällig den ersten rückgängig machen)

insbesondere das erste und das letzte Element nicht mehr gleich.

(Noch schöner ist es manchmal aber, wenn man bei solchen Gleichungsketten das Ergebnis schon kennt

[die Lehrkraft weiß es ja üblicherweise sowieso]

und "nur" noch den Weg dorthin rekonstruieren muss, also z.B. bei

= schon ein bisschen einfacher = noch einfacher = ... =

Dann geht die "Fahrt" nämlich nicht so vollständig ins Unbekannte, sondern kann man von beiden [bekannten] Seiten "aufeinander zurechnen" und zudem besser überprüfen, ob man richtig "gefahren" ist.)

Statt so ungezielt an die Aufgabe dran zu gehen, sollte man einige Vorüberlegungen anstellen:

1. "Oh je, das wimmelt ja nur so vor lauter Schwierigkeiten?" Es ist nun wahrhaft nicht ehrenrührig, sich solche Schwierigkeiten erstmal einzugestehen. Nur wer sie erkennt, hat eine Chance, sie anzugehen bzw. abzumildern.

2. "Welche Einzelschwierigkeiten liegen denn vor?" D.h., nach der ersten allgemeine Panik wird man ein wenig ruhiger und zerlegt sich das Großproblem in viele Kleinprobleme. Noch unsortiert:

   1. Brüche, ja sogar Mehrfachbrüche (in Zähler und Nenner des Gesamtbruchs stehen kleinere Brüche),

   2. ganze Zahlen, Brüche und gemischte Zahlen,

   3. Klammern zuhauf, und sogar noch schlimmer: Mehrfachklammern (eckige und runde bzw. runde in eckigen),

   4. alle Rechenzeichen dieser Welt, also : (bzw. Bruchstrich), • , + , -

   (Nebenbei: genau so ist die vorliegende Aufgabe ja auch gemeint: in den üblichen Schulbüchern werden die Probleme erst

• hübsch nacheinander,

• logisch aufeinander

• und idiotensicher voneinander getrennt

durchgenommen und geübt

[also z.B.

• erst die ganzen Zahlen,

• dann Brüche,

• dann gemischte Zahlen,

• dann die Bruchaddition,

• dann die Bruchsubtraktion,

• dann die Bruchmultiplikation,

• dann die Bruchdivision].

Die SchülerInnen werden also lange Zeit fest beim Hündchen genommen wie sonst nur bei einem Reisebegleiter, wenn man eine Pauschalurlaub gebucht hat.

Dann aber werden die  SchülerInnen urplötzlich anhand "komplexer" bzw. kombinierter Aufgaben ins kalte Wasser geworfen werden, damit sie

• alle gelernten Regeln gleichzeitig anwenden können,

• herausfinden, wann welche Regel angewandt werden muss,

• in diesem Wasser ertrinken!

Der erste Schock, der viele SchülerInnen bei ergreift, ist also durchaus beabsichtigt! Man nennt das auch "die Spreu vom Weizen trennen".)

Angenommen nun also,

• man hat sich all die Einzelprobleme schön auseinanderklamüsert

• und man beherrscht sogar alle Rechenregeln.

All das hilft einem leider noch immer nicht, sondern man muss auch wissen, in welcher Reihenfolge man vorzugehen hat

(denn die Reihenfolge ist eben nicht egal, d.h. man kann auch nicht anfangen, wo man will bzw. wo einem das kleinste Problem vorzuliegen scheint).

Da nun aber hilft ein Verfahren, wie ich es auch im Deutschunterricht bei der Analyse von Texten empfehle, nämlich das sogenannte "Zoom-Verfahren":

von groß zu klein

 Das sei vorerst tatsächlich mal anhand von Texten im Deutschunterricht erklärt:

• schon aus großer Entfernung (also sogar dann, wenn ich die Buchstaben noch gar nicht erkennen kann) sehe ich an der Länge und gegebenenfalls dem Zeilensatz, welche Textsorte (Prosa, Drama oder Lyrik) vorliegt,

• ein bisschen näher dran gehend (und noch immer nicht die Buchstaben lesen könnend) erkenne ich Absätze bzw. Strophen, also den Grobaufbau,

• noch näher dran gehend, erkenne ich z.B. bei einem Gedicht die Einzelzeilen,

• und irgendwann, ganz nah dran, erkenne ich Einzelwörter oder sogar Einzelbuchstaben.

(Nebenbei: durch das langsame Heranzoomen ist immer klar, in welchem Kontext sich jedes neu erscheinende, kleinere Element befindet! Es kann mir also eigentlich nicht passieren, dass ich

• vor lauter Bäumen

[völlig zusammenhanglosen Einzelteilen]

• den Wald nicht mehr sehe

[den Gesamttext, die Funktion der Einzelteile in ihm sowie die - wichtigen - Verbindungen zwischen ihnen].)

Dieses "Zoomverfahren" lässt sich nun durchaus auch auf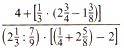

(bzw. sogar alle komplizierteren mathematischen Aufgaben)

übertragen. Nähern wir uns dazu also 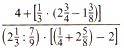mal sozusagen aus der Ferne:

• zu allererst erkennt man eine grobe Zweiteilung in Zähler über und Nenner unter dem Haupt-Bruchstrich:

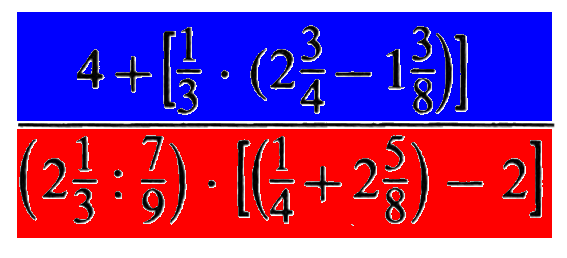
• Innerhalb (!) des Zählers (also schon genauer hinschauend bzw. näher dran) erkennt man eine grobe Zweiteilung in

  • einerseits 4 und

  • andererseits die gesamte eckige Klammer:

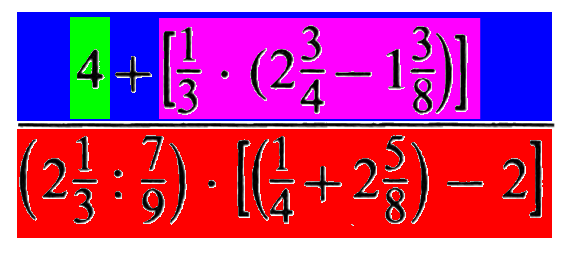
• Entsprechend erkennt man innerhalb (!) des Nenners eine grobe Zweiteilung in

  • einerseits die vordere runde und

  • andererseits die gesamte hintere eckige Klammer:

  

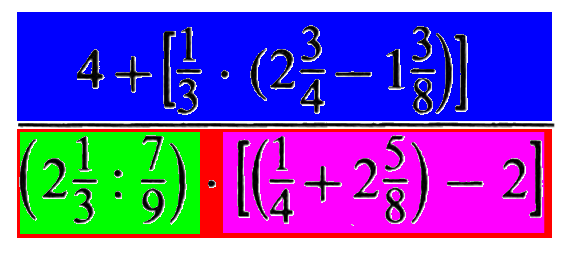
• Insgesamt haben wir also bisher:

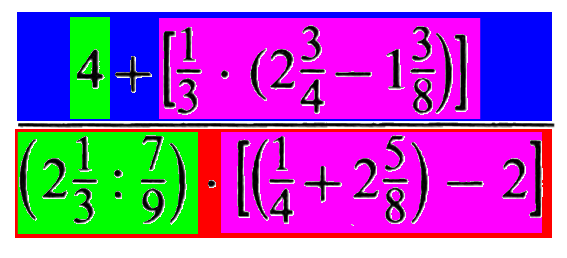
(Vorsicht: gleichfarbige Elemente oben und unten,

• also das hellgrüne Element oben und das hellgrüne unten

• sowie das violette Element oben und das violette unten,

haben keinerlei inhaltliche Gemeinsamkeit

[d.h. insbesondere, dass man sie schon gar nicht gegeneinander "kürzen" kann],

sondern ich habe sie nur gleichfarbig markiert, um

• die parallele Vorgehensweise bei Zähler und Nenner zu veranschaulichen,

• nicht allzu viele [dann nur schwer unterscheidbare] Farben zu benutzen.)

• Als nächstkleinere Elemente ergeben sich nun (nicht mehr detailliert erklärt) die gelben und die hellblauen:

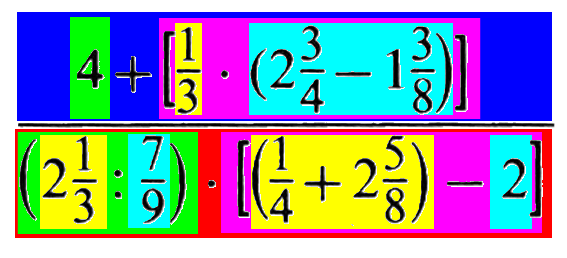
• Wenn man nun beim hellblauen Element oben und beim gelben Element rechts unten noch mal genauer hinschaut, so kann man da jeweils noch eine Zweiteilung in Orange und Olive vornehmen:

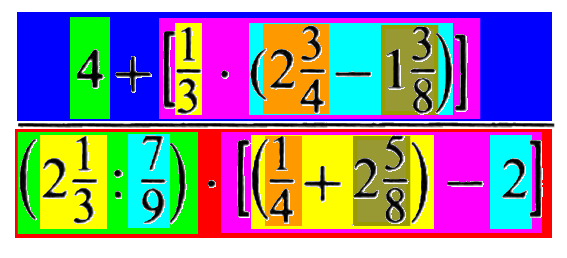
So weit vorerst!

(Nun könnte man auch noch die gemischten Zahlen [also z.B. oben in der Mitte 2 ³/₄) in ihre Einzelteile (also 2 +. ³/₄) zerlegen, aber mir scheint, dass das Schema dann doch allzu unübersichtlich würde.

Dennoch sind diese gemischten Zahlen nicht unwichtig, sondern wir werden glatt im Gegenteil sehen, dass man sogar mit ihnen anfangen muss.)

Ich verstehe sogar, wenn jemand einwendet, meine farblichen Markierungen seien auch ohne weitere Eintragungen schon unübersichtlich genug. Aber wichtiger als das (statische) Endergebnis ist der "Zoom"-Prozess, in dem diese Markierungen nacheinander erstellt wurden:

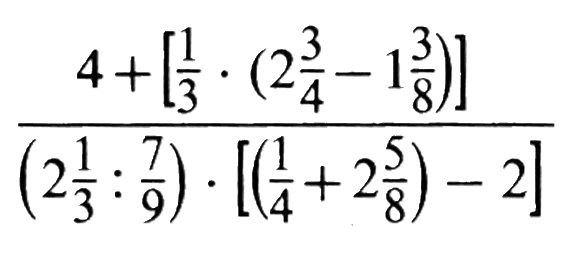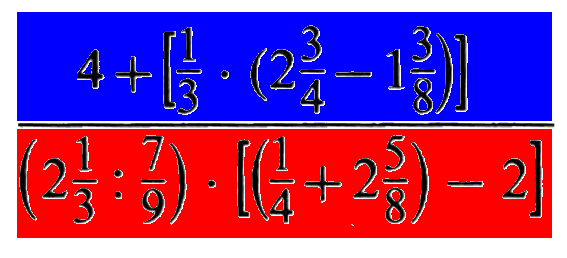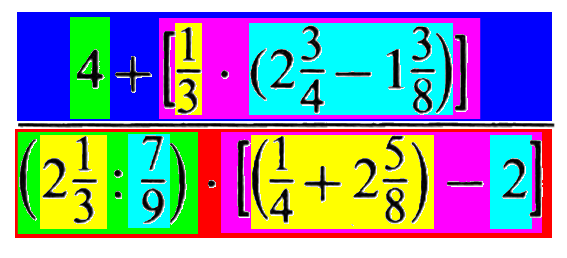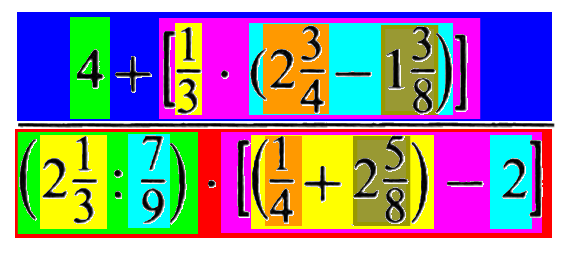
bzw. an einem Ausschnitt:

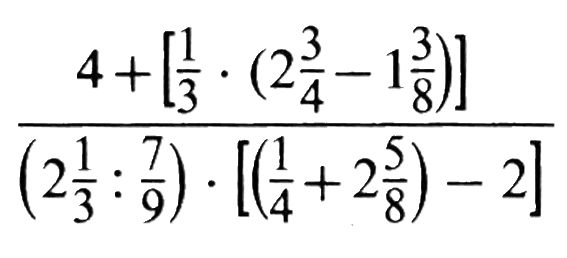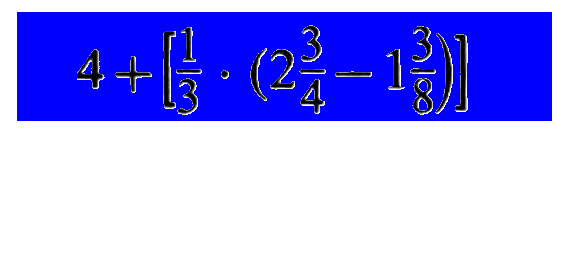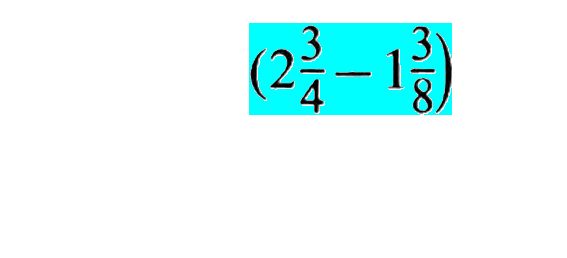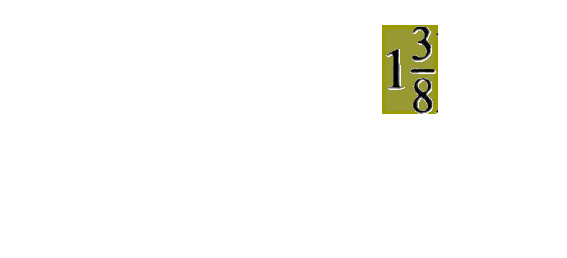
• von groß zu klein

• bzw. - wie erst jetzt deutlich wird - hübsch ineinander geschachtelt: jedes kleinere Kästchen steht ganz innerhalb jeweils größeren

(z.B. Orange ganz innerhalb von Gelb bzw. Gelb ganz innerhalb von Violett).

Was also niemals passieren darf

(bzw., wenn man mathematisch korrekt arbeitet, auch gar nicht passieren kann),

ist, dass Kästchen einander überlappen:

• erlaubt:   
   

• verboten:

Insbesondere darf das natürlich nicht bei Klammern passieren:

• erlaubt:     (   [        ] )
  

• verboten:  (   [    )     ]

(Und nebenbei: Klammern, die geöffnet werden, müssen immer auch wieder geschlossen werden [bzw. umgekehrt] - was bei Kästchen ganz selbstverständlich passiert.)

Tut mir leid, aber mit dem "Zoom-Verfahren" ist leider erst der halbe Weg gegangen, bzw. jetzt muss man ihn noch komplett zurück gehen

(also sozusagen den "Zoom" langsam wieder zurück fahren):

• von klein zu groß;

• man fängt also mit den kleinsten Elementen an

• und geht erst nach deren Bearbeitung zu den nächst größeren über.

Um es an

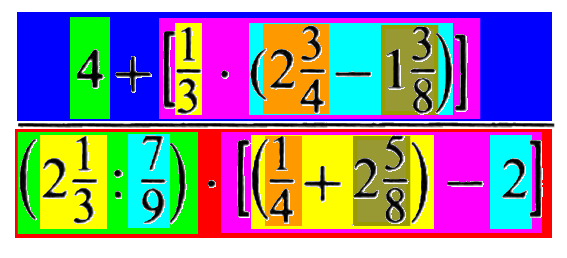
und da auch nur einem Ausschnitt zu verdeutlichen.

Der Zoom läuft nun also, beginnend bei ganz rechts oben im Zähler beginnend, rückwärts:

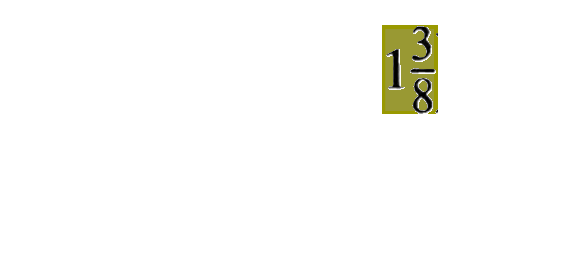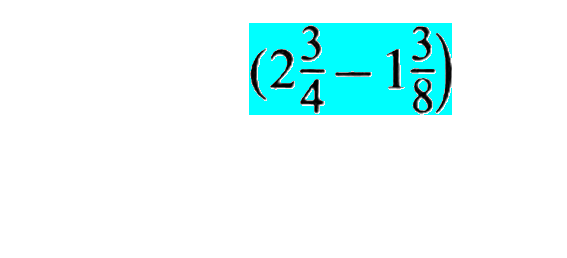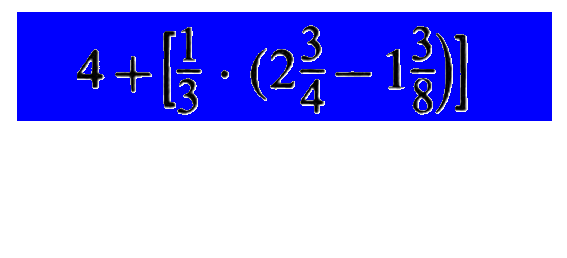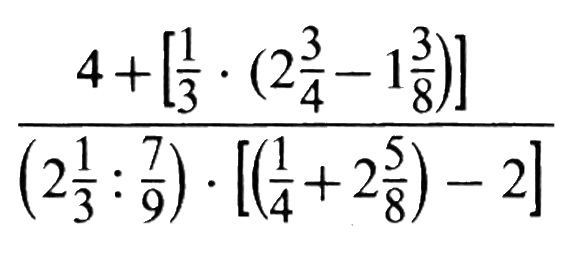
Nun stimmt diese Abfolge aber nur ungefähr: in Wirklichkeit muss natürlich erst mal "vereinfacht", d.h. in einen "normalen" Bruch, also , überführt werden, und dementsprechend wird dann immer mit vereinfachten Elemente weitergerechnet.

Und dann, so behaupte ich hier einfach, verschwinden nacheinander systematisch alle Schwierigkeiten und kommt am Ende heraus.

Ich bin mir durchaus bewusst, dass das Verfahren keineswegs so einfach ist, wie es jetzt vielleicht erscheinen mag: mein Vormachen ist allzu suggestiv, weil ich ja schon den Blick für die jeweils richtigen Elemente habe.

Aber das Verfahren lässt sich ja systematisch mit SchülerInnen üben, beginnend bei einfacheren Beispielen: statt immer sofort wild zu rechnen, werden viele Aufgaben durchgenommen, in denen systematisch (mit Buntstift) Kästchen ineinander gemalt werden - und oftmals gar nicht gerechnet wird.

Beim Vereinfachen (also nach der Kästchenerstellung) ist AnfängerInnen dringend zu empfehlen, nicht an allen Ecken und Kanten gleichzeitig anzufangen

(oder sogar gleichzeitig mit völlig verschiedenen Problemen, also beispielsweise gleichzeitig Bruch- und Klammerrechnung),

sondern

(auf die "Gefahr" hin, sehr viel unverändert abschreiben zu müssen)

mit einem einzigen Problem anzufangen, also z.B. nur mit der Umformung von in .

Dabei ändert sich an der Gesamtstruktur nur an einer einzigen Stelle (nämlich bei ) etwas, weshalb ich sogar empfehle,

• vor der Umformung von in die ansonsten unveränderte Gesamtstruktur 1:1 zu kopieren und nur an der zu verändernden Stelle eine Lücke zu lassen

(nur am Zähler gezeigt: )

• und dann erst statt den "normalen" Bruch einzusetzen:

(also                              )

(Nebenbei: weil ich genau weiß, wie schlampig ich oftmals bin, zwinge ich mich sogar dazu,

• das Unveränderte akkurat untereinander abzuschreiben

• und nach dem Abschreiben nochmals detailliert zu überprüfen, ob ich auch wirklich alles richtig abgeschrieben habe:

eine einzige verlorene Klammer, und schon ist alles falsch!)

Wenn man schon geübter ist

(und das ist sogar dem "Vollprofi" zu empfehlen, weil auch er sich gerne schnell verzettelt!),

kann man gleichartige Probleme gleichzeitig angehen, also z.B. im ersten Schritt alle gemischten Zahlen in "normale" Brüche überführen:

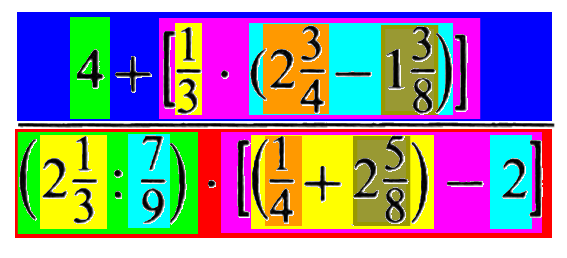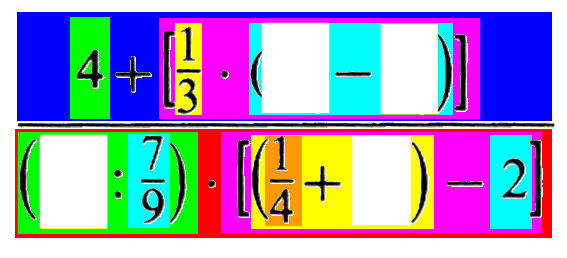
Tut mir leid, aber beim Vereinfachen von solchen Bruchmonstern wie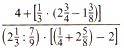

(über deren Sinn man sich ja durchaus streiten kann)

ist Kreativität nun mal ausgesprochen unerwünscht, sondern helfen nur gnadenlose (stumpfe) Ordnung und Systematik.

Ich hatte anfangs behauptet:

"[Ich meine], dass die Fertigkeit, mit  - pars pro toto - umgehen zu können, auf andere Art sinnvoll ist, als es im üblichen Unterricht betrieben wird."

Jetzt lässt sich zeigen, warum das sogar weit über solche Bruchmonster wie 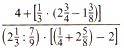und überhaupt Brüche hinaus sinnvoll ist: man trainiert damit einen Blick für zusammenhängende Elemente bzw. einen "Parser-Blick" (vgl. auch  ).