wie viel muss/darf man vorgeben?

Vgl. auch

Anlass meiner Überlegungen hier war ein "Mathetag" an "meiner" Schule, an dem  ich mit einer Schülergruppe das Thema "Zahlen" behandelt habe. Krönender Abschluss war dabei das "Cantorsche Diagonalverfahren" zur Abzählbarkeit der rationalen Zahlen (Brüche), also

Hier sollen nicht die mathematischen Hintergründe genauer behandelt werden

(vgl. dazu Bild),

sondern überlegt werden soll "nur", welche Vorgaben unerlässlich sind, damit SchülerInnen danach dennoch weitestgehend selbstständig auf das Diagonalverfahren kommen können:

so viel wie nötig, so wenig wie möglich.

Dabei ist das Cantorsche Diagonalverfahren allemal ein reizvoller Anlass, da es paradoxerweise genial einfach ist:

Aber zwischen den beiden Extremen "genial/einfach" scheint eine riesige Lücke zu klaffen, d.h. es scheint unmöglich, selbst "drauf" zu kommen.

(Nebenbei: warum eigentlich kommt das Cantorsche Diagonalverfahren im Standardunterricht nie vor?:

  1. vielleicht tatsächlich, weil es so uneinholbar einfach ist, man es also angeblich nur fertig vormachen bzw. konsumieren und es demnach etwa in einer Klausur nur stumpf nachmachen kann;
  2. , weil die Feststellung der "Abzählbarkeit der rationalen Zahlen" keinen "Nährwert" für alle folgende Schulmathematik hat?
  3. , weil die (Über-)Abzählbarkeit, also der Vergleich zweier unendlicher Menge, tatsächlich oder angeblich das Auffassungsvermögen (nicht nur) von SchülerInneN Überfordert?

Ich meine hingegen, dass zumindest 1. und 3. keine stichhaltigen Gründe sind.)

Warum also das Cantorsche Diagonalverfahren, das doch immerhin einer der absoluten Geniestreiche der Mathematik ist, und damit eine besonders schöne mathematische Denkweise den SchülerInnen vorenthalten?

Nur ist es aber witzlos, es einfach fertig vorzumachen. Dann bleibt den SchülerInneN tatsächlich nur, es hinzunehmen und zu denken: "Da wäre ich nie drauf gekommen."

Welch ein Stolz aber, wenn sie es nach einigen wenigen Anregungen selbst (nach-)entdeckt haben!

(Das muss nicht der Stolz jedes Einzelnen sein, sondern es gibt auch einen "Kollektivstolz", wenn "nur" einige wenige es geschafft haben, was ja doch immerhin zeigt: "Wir können sowas auch, man muss also kein Megagenie wie Cantor sein.")

Vorweg sollte man wohl klar machen, was für ein unüberschaubares Kuddelmuddel die Brüche doch scheinbar sind:

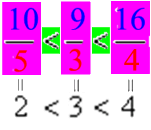  1. sind viele Brüche identisch, obwohl sie doch unterschiedlich aussehen, ja, sogar eine ganze Zahl kann sich hinter einem Bruch verstecken. Vgl. etwa 3 =  = = ...
  2. ist die Größenordnung von Brüchen bzw. ihr Verhältnis zueinander kaum zu erkennen. So gilt z.B. , obwohl doch 10 > 9 < 16 und 5 > 3 < 4 ist.

Und doch steckt hinter 2. schon ein Teil der (cantorschen) Lösung, wenn man überlegt, in welchen Spezialfällen man das Verhältnis zweier Brüche dennoch sehr einfach erkennen kann, nämlich dann,

(Und wenn Brüche nicht bereits gleichnamig sind, muss man sie eben - was immer geht! - mittels Erweitern gleichnamig machen, d.h. auf den [selben] "Hauptnenner" bringen.)

Die beiden Ergebnisse und lassen sich aber kombinieren zu

oder jetzt ohne die Kleiner-/Größerzeichen:

,

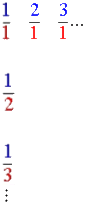womit sich hinter dem scheinbaren Kuddelmuddel der Brüche doch noch eine (zweidimensionale) Ordnung zeigt. Und mir scheint ja in der Tat, dass es reicht, den SchülerInnen das knappe Muster

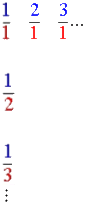
zu zeigen, damit sie es selbstständig zu

vervollständigen können.

(Ich würde all dies mit fertigen Bruchkärtchen machen, die die SchülerInnen zu Mustern anordnen.)

Nun müssen die SchülerInnen "nur" noch wie in

den Weg durch das Labyrinth finden, und zwar natürlich, ohne dass man ihnen diesen Weg vormacht.

Ihnen muss nur klar sein, was gesucht ist:

  1. mit

haben wir zwar immerhin schon eine zweidimensionale Anordnung der (aller!) Brüche, aber gesucht ist eine eindimensionale Anordnung bzw. ein Hintereinander. Gesucht ist also ein "stetiger" Weg durch alle Brüche ohne jedes Absetzen. Eine schöne Metapher dafür ist ein Bindfaden, den man z.B. wortwörtlich auf dem 1/1-Kärtchen links oben befestigt und danach Über alle anderen Bruchkärtchen legen muss. Vorstellbar ist da etwa, dass auf jedem Bruchkärtchen ein "Pinörkel" befestigt ist, um den der Bindfaden herum gelegt werden muss.

  1. muss es ein "systematischer" Weg sein, von dem klar ist, dass er, obwohl man nur den endlichen Anfang zeichnen kann, auch unendlich so weiter geht und alle (unendlich viele!) Brüche durchläuft.

Es gibt verschiedene solche Wege, und in der Mathe-AG, die der Anlass der hier vorliegenden Überlegungen war, fand ein Schüler tatsächlich schnell einen "ungewöhnlichen" Weg und eine Schülerin kurz drauf das typische "Diagonalverfahren"

.

Es "geht" also durchaus in der Schule, und zwar, wie der Mathetag gezeigt hat, auch schon in einer 9. Klasse.