"that's mathematics" : die Winkelsumme in ALLEN Dreiecken ist 180⁰

(Im Vergleich damit ist die nächst"härteste" Wissenschaft, nämlich die Physik, bereits ein "Weichei", da sie letztlich rein statistisch verfährt: "bisher traf's immer [und auch nur im Rahmen der Messgenauigkeit] zu".)

Nun weiß aber jedeR MathematikerIn natürlich, dass bereits die Aussage "die Winkelsumme in ALLEN Dreiecken ist 180⁰" in der Überschrift falsch ist, wie ja bereits das Bild 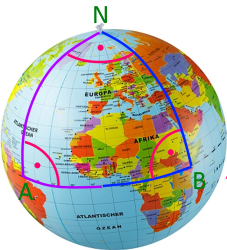   beweist:

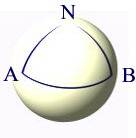
wenn zwei Personen

• sich am Nordpol N in einem Winkel von 90⁰ trennen und

• jeweils "ihren" Meridian entlang bis zum Äquator, also bis zu den Punkten A und B gehen,

• dann aber auf dem Äquator aufeinander zu, bis sie sich treffen, 

dann entsteht offensichtlich ein Dreieck, bei dem in jedem Eckpunkt N, A und B ein Winkel von 90⁰ "sitzt", so dass die Winkelsumme offensichtlich 90⁰ + 90⁰ + 90⁰ = 270⁰ , also erheblich größer als 180⁰ ist.

Und schon sind wir mitten in dem, was Mathematik eigentlich "ist":

1. bedeutet (wie wir noch sehen werden) die neue Aussage

"die [anfängliche/alte] Aussage »die Winkelsumme in ALLEN Dreiecken ist 180⁰«
in der Überschrift [ist] falsch"

keineswegs, dass es GAR KEINE Dreiecke mit der Winkelsumme 180⁰ gibt, sondern "nur", dass es

• eventuell sehr wohl mindestens ein, wenn nicht gar (unendlich) viele Dreieck(e) mit der Winkelsumme 180⁰ gibt,

• dass aber nicht ausnahmslos ALLE Dreiecke die Winkelsumme 180⁰ haben.

  Denkbar wäre,

• dass in (unendlich) vielen Dreiecken eine ANDERE Winkelsumme als 180⁰ vorliegt,

• aber auch, dass es nur eine EINZIGE Ausnahme gibt, nämlich : ein EINZIGES Gegenbeispiel reicht aber völlig aus, um die Behauptung "(ausnahmslos) ALLE" zum Einsturz zu bringen.

Und schon zeigt sich das nächste Problem:

2. Wie soll es denn

• einerseits eventuell unendlich viele Dreiecke mit der Winkelsumme 180⁰

• und andererseits dennoch noch eine oder mehrere Ausnahmen geben?

Heißt "unendlich viele" nicht doch "alle", so dass keine einzige

(geschweige denn mehrere oder gar wiederum unendlich viele)

Ausnahme(n) mehr möglich ist/sind?

Die Lösung dieses scheinbaren Widerspruchs ist ebenso einfach wie

(dennoch oder gerade deswegen)

genial - und vielen Laien wohl fremd. Sie lässt sich schön an einer Analogie zeigen:

• es gibt offensichtlich       unendlich viele    gerade natürliche Zahlen 2, 4, 6, 8, 10 ...,

• zusätzlich aber ebenfalls unendlich viele ungerade natürliche Zahlen 1, 3, 5, 7, 9, 11...

Die Unendlichkeit einer Menge schließt also nicht aus, dass "die andere Hälfte" auch unendlich groß ist.

3. Viele Laien werden vermutlich das oben gezeigte Gegenbeispiel als spitzfindig-hinterhältig empfinden:

"Da kann ich ja die bescheuertste gekrümmte Form, also z.B. auch , wählen, und wen wundert's da noch, dass sich dann auch irgendwelche bescheuerten ANDEREN Winkelsummen ergeben?!"

Unsere hypothetischen Laien stehen da keineswegs allein da, sondern befinden sich in bester Gesellschaft: an solch eine ("nichteuklidische") Geometrie auf gekrümmten Flächen haben die Mathematiker auch jahrtausendelang nicht gedacht, und als sie dann doch langsam aufkam, haben sich anfangs auch viele prominente Mathematiker dagegen gewehrt.

(Nebenbei: das Dreieck in hat eine Winkelsumme, die kleiner als 180⁰ ist.
Und es sei auch kurz ergänzt, dass solche Dreiecke auf gekrümmten Flächen nicht nur eine bescheuerte/nette mathematische Idee sind, sondern in der Relativitätstheorie durchaus ihre Anwendung gefunden haben.

Überhaupt ist die nichteuklidische Geometrie höchstens auf den ersten Blick "bescheuert". Auf den zweiten öffnet sich mit ihr aber eine ganz eigene Ästhetik des Dreidimensionalen und der biegsamen Flächen.)

Man wird den Dreiecken in und nicht absprechen können, dass sie drei (!) Ecken (!) haben. Und dennoch stört den "gesunden Menschenverstand" da vermutlich doch, dass die Seiten dieser Dreiecke keine geraden Strecken sind.

(Wäre man bereit, auch noch als "Dreieck" zu bezeichnen?)

Der Normalfall für einen Laien ist also, dass

• ein Dreieck auf einer Ebene (einem Platt Papier) gezeichnet ist und somit

• gerade Seitenstrecken hat.

Die weiter aufrecht erhaltene Behauptung

"die Winkelsumme in ALLEN Dreiecken ist 180⁰"

ist also nicht mehr allgemeingültig

(da muss sich sogar die Mathematik weise beschränken!),

sondern wird "nur" noch für ALLE Dreiecke in der EBENE aufrecht erhalten.

Dabei ist "nur" dennoch allerhand: es ist die Rede von ALLEN (unendlich vielen!) Dreiecken in der Ebene, also

• ALLEN bislang gezeichneten,

• ALLEN noch nicht gezeichneten,

• klitzekleinen (bei denen der genaueste Bleistift versagt),

• riesig großen, die auf kein Papier der Welt passen, also z.B.

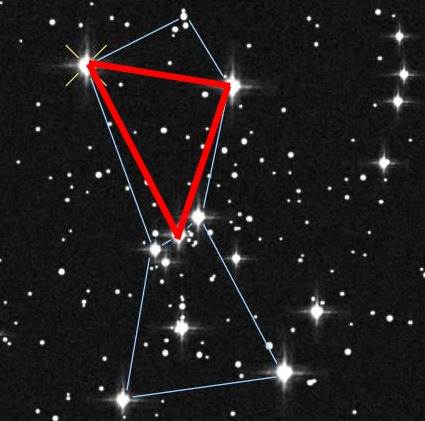
(wobei hier der Einfachheit halber mal vorausgesetzt sei, was gar nicht so selbstverständlich ist:
dass nämlich solch ein Dreieck in einer Ebene liegt)

Auch das könnte (sollte!) einen Laien

(und nach wie vor auch Fachleute!)

maßlos erstaunen, denn man möchte doch denken:

1. Wie kann man denn etwas für Dreiecke beweisen, die zu klein oder zu groß sind, um sie zu zeichnen? Wie kriegt man diese Dreiecke denn überhaupt zu "fassen"?

2. Wenn man etwas für ALLE ebenen Dreiecke beweisen will, so muss man doch auch ALLE nacheinander "erledigen". Da "ALLE" aber UNENDLICH VIELE sind, wird man auch UNENDLICH LAngE beschäftigt sein, also NIE FERTIG WERDEN!?

Um so erstaunlicher ist es, dass der Beweis

• überhaupt in endlicher, ja sogar sehr kurzer Zeit möglich ist

• und wie äußerlich "schlampig" er angefertigt wird.

Wohlgemerkt: die EINZIGE konkrete Eigenschaft, die wir nach unseren "schlechten" Erfahrungen mit zulassen, ist, dass das Dreieck in einer EBENE liegt.

Wir zeichnen also auf einem (ebenen!) Blatt Papier IRGENDEIN Dreieck mit möglichst "unkonkreten" Maßen

(weil MathematikerInnen vorgewarnt sind, sollte dieses Dreieck weder gleichseitig noch gleichschenklig noch rechtwinklig aussehen).

Da zudem jedeR MathematikerIn weiß, dass man sowieso kein Dreieck mit absolut genau geraden Seitenstrecken zeichnen kann

(unterm Mikroskop ist selbst die scheinbar geradeste Linie doch wieder zackelig),

reicht eine schlampige Planskizze:

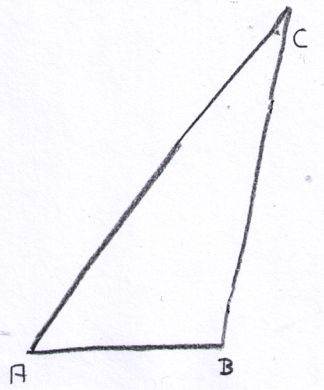
Auch das ist typisch Mathematik: das eigentliche, wirklich genaue Dreieck existiert eh nur in unserem Kopf (!), und die Planskizze dient einzig und allein dazu, überblick insbesondere bei mehreren aufeinander folgenden Schritten zu behalten (vgl. ).

Der nun folgende Beweis ist

• nicht nur einer der ältesten der gesamten Mathematik,

• sondern auch (vgl. oben) ebenso einfach wie

  (dennoch oder gerade deswegen)

  genial. Ich "befürchte", dass ich nie auf diese Idee gekommen wäre, was bei mir allerdings nicht zu Minderwertigkeitskomplexen, Neid oder gar Missgunst führt, sondern nur meine Bewunderung für die Entdecker dieses Beweises erhöht.

Wir

• legen nun parallel zur Grundstrecke AB eine Gerade ------- durch C,

• verlängern die Seiten AC und BC nach oben hin

• und zeichnen die Winkel α, β und γ des Dreiecks auch oberhalb der Parallelen ein

(man mache sich dabei klar, dass die oben auftauchenden Winkel genauso groß wie die ursprünglichen Winkel des Dreiecks sein müssen; vgl. Stufen- bzw. Scheitelwinkel):

Offensichtlich ergeben die Winkel α, β und γ OBEN zusammen genau 180⁰ - und also auch die URSPRÜNGLICHEN Winkel α, β und γ des Dreiecks.

Wir überprüfen nochmal: in der gesamten Beweisargumentation tauchten kein einziges Mal irgendwelche konkreten Maße des Dreiecks (Winkel, Seitenlängen) auf, so dass dieser Beweis wirklich für ALLE ebenen Dreiecke gilt!

Es ist tatsächlich gelungen, in sehr kurzer (endlicher!) Zeit UNENDLICH viele (ALLE) Fälle zu "erschlagen".

Erwähnenswert ist zuguterletzt, dass die Winkelsumme bei ebenen Dreiecken immer exakt 180⁰ ist, bei Dreiecken auf krummen Flächen allerdings variieren kann, also z.B. nicht immer wie oben 270⁰ ist.

Die Einschränkung auf ebene Dreiecke "erwischt" eben doch die interessantesten Fälle (eine einheitliche Regel).

PS: vgl.