
Der Titel des Buchs
 ist wohl eine
Kurzform des Aussagesatzes „[Hier wird erklärt,] Wie Mathematiker ticken“.
Vielleicht hört man da aber doch auch die rhetorische Frage „Wie ticken
Mathematiker?“ mit der unterstellten Antwort „Mathematiker ticken nicht richtig“
ist wohl eine
Kurzform des Aussagesatzes „[Hier wird erklärt,] Wie Mathematiker ticken“.
Vielleicht hört man da aber doch auch die rhetorische Frage „Wie ticken
Mathematiker?“ mit der unterstellten Antwort „Mathematiker ticken nicht richtig“
(und ihre „Gedankenwelt“ ist - gelinde gesagt - absonderlich)
heraus: ein populäres Vorurteil, auf das der Autor also eventuell bewusst anspielt - und das er mit dem Buch zu entkräften versucht.
(Ich habe mehrfach von Lesern meiner Internetseiten gehört, dass sie schon in ihrer Schulzeit, aber auch noch lange danach die Mathematik gehasst und Mathematiker für wichtigtuerische Spinner gehalten haben, jetzt in fortgeschrittenem Alter aber doch gerne mal wüssten, „wie Mathematiker wirklich ticken“.)
Ein (scheinbares) Musterbeispiel dafür, dass Mathematiker „nicht richtig
ticken“, ist eines der berühmtesten Bücher der Mathematik, nämlich
 von
von
 und
und
 .
.
Schon die Anspielung auf Isaac Newtons berühmtes Buch
 zeigt den enormen
Anspruch des Buchs von Russell und Whitehead:
zeigt den enormen
Anspruch des Buchs von Russell und Whitehead:
Es scheint das Schicksal vieler berühmter
(und wirkungsmächtiger!)
Bücher zu sein, dass
(außer hochspezialisierten, "durchgetickten" Fachleuten)
"keine Sau" sie gelesen hat:
 von
Johannes Kepler
von
Johannes Kepler 
 von Charles Darwin
von Charles Darwin  : in diesem
Fall ist den meisten Laien vermutlich sogar der Name des Autors James Clerk
Maxwell unbekannt. Und doch ist er
: in diesem
Fall ist den meisten Laien vermutlich sogar der Name des Autors James Clerk
Maxwell unbekannt. Und doch ist er
 . Dabei ist "everything"
zwar ein bisschen arg dick aufgetragen, aber Maxwell hat doch allerlei
verändert bzw. überhaupt erst möglich gemacht, nämlich sämtliche
Elektromotoren und Dynamos sowie allen Funk
. Dabei ist "everything"
zwar ein bisschen arg dick aufgetragen, aber Maxwell hat doch allerlei
verändert bzw. überhaupt erst möglich gemacht, nämlich sämtliche
Elektromotoren und Dynamos sowie allen Funk
 , und das mit nur
vier Gleichungen
, und das mit nur
vier Gleichungen 
(die es allerdings in sich haben).


 :
: weil das Buch weitgehend in der Sprache der mathematischen Logik geschrieben ist, sieht es hunderte von Seiten etwa so aus:
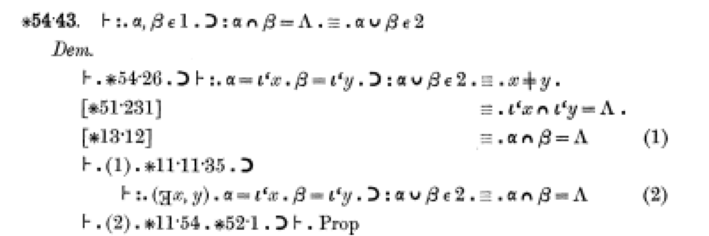
Nach geschlagenen 360 Seiten voll mit solchem Fachchinesisch passiert dann aber Folgendes:

Urplötzlich
 wird da also das äußerst
Komplizierte ganz einfach, denn die Autoren haben soeben bewiesen, dass
wird da also das äußerst
Komplizierte ganz einfach, denn die Autoren haben soeben bewiesen, dass
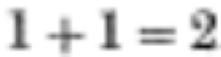
ist.
Nun gibt es allerdings zwei gegensätzliche Bewertungen der
Erkenntnis 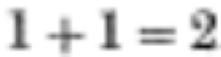 :
:
 der Mathematik
gelungen, denn wie wir unten sehen werden, ist
der Mathematik
gelungen, denn wie wir unten sehen werden, ist
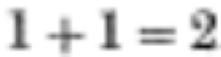 der Beginn
aller
Zahlen.
der Beginn
aller
Zahlen.
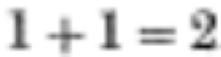 ist der
endgültige Beweis (!), dass Mathematiker nicht richtig ticken, denn es weiß
doch jedes Kind, dass
ist der
endgültige Beweis (!), dass Mathematiker nicht richtig ticken, denn es weiß
doch jedes Kind, dass
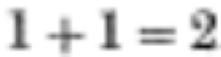 ist.
ist.
Der Beweis Russells und Whiteheads, dass
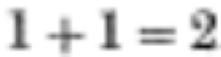 gilt, war aber nur
ein erster Schritt auf dem Weg zum großen Ziel, die gesamte Mathematik
vollständig logisch zu erklären: ein Ziel, das nach gigantischer Arbeit aber
tragisch verfehlt wurde:
gilt, war aber nur
ein erster Schritt auf dem Weg zum großen Ziel, die gesamte Mathematik
vollständig logisch zu erklären: ein Ziel, das nach gigantischer Arbeit aber
tragisch verfehlt wurde:
Wir werden unten im Hauptteil auf
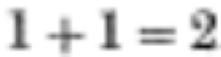 zurückkommen.
zurückkommen.
Hier aber noch einige Anmerkungen:
 gelesen oder
genauer: mit Kommilitonen mühsam erarbeitet
gelesen oder
genauer: mit Kommilitonen mühsam erarbeitet
 durchgerechnet
und vielleicht sogar ansatzweise verstanden
durchgerechnet
und vielleicht sogar ansatzweise verstanden(inzwischen aber alles längst wieder vergessen).
 war noch
erstaunlich einfach, an
war noch
erstaunlich einfach, an
 haben wir uns aber
wegen der uns bis dahin unbekannten “Tensorrechnung“ ein Jahr lang die Zähne
ausgebissen.
haben wir uns aber
wegen der uns bis dahin unbekannten “Tensorrechnung“ ein Jahr lang die Zähne
ausgebissen.
Alle anderen oben genannten berühmten Bücher habe ich aber nicht gelesen,
und insbesondere bei Russels und Whiteheads
 hätte ich
vermutlich auch nicht die geringste Chance, dieses Buch zu verstehen.
hätte ich
vermutlich auch nicht die geringste Chance, dieses Buch zu verstehen.
Aus der enormen Kompliziertheit dieser Bücher schließe ich aber nicht, dass die Autoren nicht richtig ticken, sondern folgt bei mir eine große Bewunderung „aus der Ferne“! Ich kann bestens damit leben, dass es Menschen gibt, die (zumindest in ihrem Fachgebiet) erheblich intelligenter sind als ich und dass ich „nur“ gutes Mittelmaß bin.
 wäre wohl das einzige der genannten Bücher, das ich auf Anhieb
verstehen könnte.
wäre wohl das einzige der genannten Bücher, das ich auf Anhieb
verstehen könnte.
Man kann nicht alle (oben genannten) Bücher lesen, und
schon gar nicht muss man das (unbedingt im Original!?). Aber es
gibt populärwissenschaftliche "Hintertreppen"


 zu berühmten
mathematisch-naturwissenschaftlichen Büchern (vgl.
zu berühmten
mathematisch-naturwissenschaftlichen Büchern (vgl.
 ), und
), und
 und
die
und
die 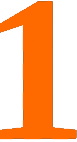 :
:die Dezimalzahlen lassen sich im Binärsystem
(mit dem alle Computer rechnen:
allesamt ausschließlich mit Nullen und Einsen darstellen. Z.B. schreibt sich

(im Binärsystem gilt also nicht
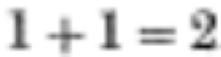 , und somit ist
, und somit ist
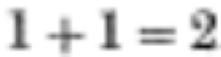 eben doch nicht so
selbstverständlich, wie man denken könnte),
eben doch nicht so
selbstverständlich, wie man denken könnte),

Ansonsten aber lassen sich alle (natürlichen) Zahlen ausschließlich aus Einsen erschaffen:
wenn erstmal
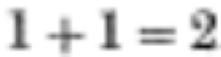 gilt (s.o.), so
folgt:
gilt (s.o.), so
folgt:
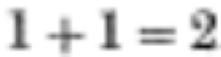
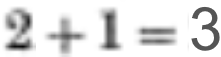
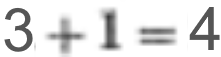
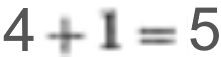
Ein Problem ergibt sich im Dezimalsystem erst bei
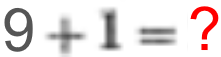 , denn für das Ergebnis
? haben wir im Zehnersystem
, denn für das Ergebnis
? haben wir im Zehnersystem
(Nebenbei: als Reste des früher üblichen Zwölfersystems
[vgl. „Dutzend“]
haben wir nur bis „zehn, elf, zwölf“ eigene Namen, denn danach folgen zusammengesetzte Namen, nämlich „drei-zehn, vier-zehn ...“.)
Um nun das Ergebnis ?
dennoch mit Ziffern aufschreiben zu können, benötigen wir erstmals zwei
Ziffern, nämlich zusätzlich zur
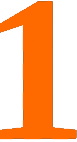 auch noch die
auch noch die
 :
:
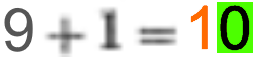
... wobei die Kombination der beiden Ziffern 1 und 0 in der Schreibweise 10 Folgendes bedeutet: 1 • zehn + 0 • 1
Die
 und
die
und
die
 sind also die
Atome (Urelemente), aus denen sich
alle anderen Zahlen (Moleküle
sind also die
Atome (Urelemente), aus denen sich
alle anderen Zahlen (Moleküle
 ) zusammensetzen
lassen.
) zusammensetzen
lassen.
mit den Zahlen
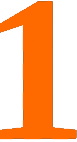 und
und
 kann man besonders einfach rechnen
kann man besonders einfach rechnen |
... und wider alle Erwartung
“warum mit einer 2 rechnen, wenn eine 0 oder 1 reicht?!“
Und wie wir gleich sehen werden, ist das Rechnen mit einer 0 sogar noch einfacher als das mit einer 1, woraus folgt:
 :
:
|
17 ,4183 + 1 = 18 ,4183 | |||
|
17 ,4183 - 1 = 16 ,4183 | |||
|
17,4183 • 1 = 17,4183 | allgemein: x • 1 = x |
besonders einfach
 |
|
|
17,4183 : 1 = 17,4183 | allgemein: x : 1 = x |
besonders einfach
 |
 :
:
|
17,4183 + 0 = 17,4183 | allgemein: x + 0 = x |
besonders einfach
 |
|
|
17,4183 - 0 = 17,4183 | allgemein: x - 0 = x |
besonders einfach
 |
|
|
17,4183 • 0 = 0 | allgemein: x • 0 = 0 |
besonders einfach
 |
|
|
17,4183 :
0 =
|
besonders schwierig: das Teilen durch 0 ist grundsätzlich verboten; aber dieser Fall kommt im Folgenden nie vor (sondern nur beim Tangens, Cotangens und gebrochen rationalen Funktionen) |
 ist naheliegend, die
ist naheliegend, die
 hingegen nicht - und deshalb genial.
hingegen nicht - und deshalb genial. :
:




 bzw.
bzw.
 ,
,
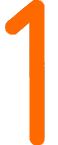
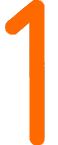 ,
,d.h. für jeden realen einzelnen Menschen
 eine
eine 
(vgl. eine
Frau, ein Mann,
ein Kind).
Ganz anders ist das aber bei der
 :
:Wieso sollte man
Um so genialer war es, das trotzdem zu tun
(und sich damit all die oben gezeigten Vorteile der 0 einzuhandeln).
Die Schreibweise
 ist äußerst passend: ein Loch ist
nichts mit etwas
drumherum:
ist äußerst passend: ein Loch ist
nichts mit etwas
drumherum:
Ich glaube tatsächlich, dass die Erfindung der
 eine der
eine der
 war
war
(was aber im üblichen Schulunterricht nie vorkommt).
Kein Wunder also, dass es
 nur
ein einz(!)iges Buch gibt:
nur
ein einz(!)iges Buch gibt:





 ..., absieht),
..., absieht), aber mindestens zehn Bücher:
aber mindestens zehn Bücher:










Mathematiker sind innig verliebt in Funktionen, die in zwei Formen vorkommen können:
Funktionsgleichungen
 ;
;Funktionsgraphen haben
Wichtig dabei ist: z.B. die Funktionsgleichung f: y = x2 und
der Funktionsgraph 
(es ist ja sowieso eine Hauptbeschäftigung der Mathematiker zu zeigen, dass
Da beide Darstellungsweisen ihre jeweiligen (nur umgekehrten) Vor- und
Nachteile haben, ist es ein zentrales Anliegen der Mathematiker bei Funktionen, die
beiden Schreibweise hin und her zu übersetzen. Vgl. ![]()
 oder
oder  .
.
Und jetzt tatsächlich endlich nähern (!) wir uns unserem eigentlichen Thema:
| einfache (?) Punkte im Koordinatensystem |
So ![]() sein mag, so macht es vielen Schülern doch immer wieder Schwierigkeiten,
und zwar gerade in den (scheinbar) einfachsten Fällen.
sein mag, so macht es vielen Schülern doch immer wieder Schwierigkeiten,
und zwar gerade in den (scheinbar) einfachsten Fällen.
Schauen wir uns an, wie es vermutlich zu diesen Schwierigkeiten kommt bzw. worin diese Schwierigkeiten bestehen.
Um zu einer vorgegebenen Funktionsgleichung den zugehörigen Funktionsgraphen zu finden
(ihn sich aber nicht gleich komplett vom Computer anzeigen zu lassen),
ist es ratsam,
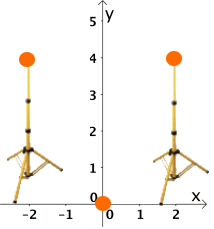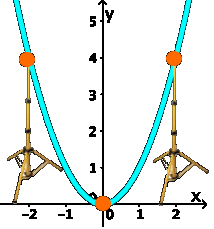
(wobei es hilfreich ist, schon vorweg zu wissen, wie die Funktionsgraphen bestimmter Funktionenklassen [z.B. quadratischer Funktionen] ungefähr aussehen [z.B. parabelförmig]).
Nun besteht ein (stetiger) Funktionsgraph allerdings aus unendlich vielen Punkten, womit sich die Frage stellt, ob es
(und wie viele),
(am besten möglichst wenige)
besonders geeignete Punkte gibt
(und was „besonders geeignet“ eigentlich bedeutet: zu was [besonders] geeignet?).
Oder vom Ende aus gefragt: in der Schule werden bis zum
 „Nullstellen“ berechnet. Aber
warum eigentlich bzw. warum gerade
diese?
„Nullstellen“ berechnet. Aber
warum eigentlich bzw. warum gerade
diese?
(... eine Frage, die im üblichen
Mathematikunterricht nie gestellt wird. Da fällt alles fertig vom Himmel
 und wird nicht
hinterfragt.)
und wird nicht
hinterfragt.)
Ein Beispiel für geeignete Punkte:
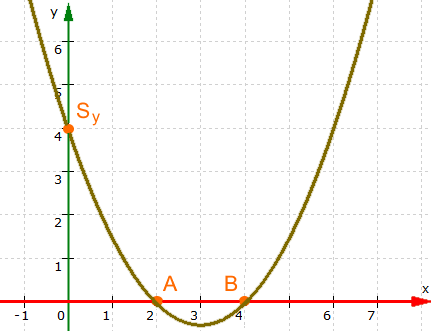
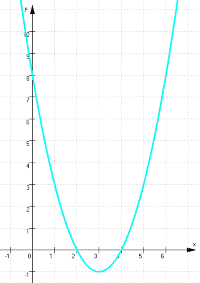
gegeben sei die Funktion mit der Funktionsgleichung y = 0,5x2 - 3x + 4
Da ist es hilfreich, vorweg (also ohne jede Rechnung) zu wissen:
(wobei wir allerdings noch nicht an der Funktionsgleichung ablesen können, wie weit die Parabel nach rechts verschoben wird).
Mit all dem kennen wir vorweg
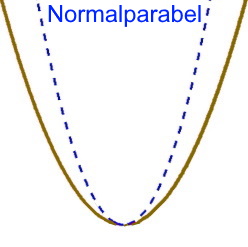 .
.
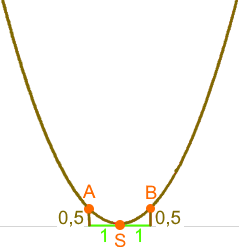
(abgesehen von seiner Rechtsverschiebung)
noch nicht seine genaue Lage:
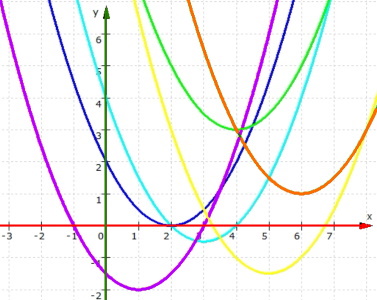
Alles wird aber ganz einfach, wenn wir den Scheitel-/Tiefpunkt S kennen, der also ein "besonders geeigneter" Punkt ist.
Diesen Scheitel- bzw. Tiefpunkt S kann man auf zwei Arten ermitteln:
Wenn man erstmal S ( 3 | - 0,5 ) kennt, ist das Zeichnen des Funktionsgraphen
(sowohl seiner Form als auch seiner Lage)
ganz einfach:
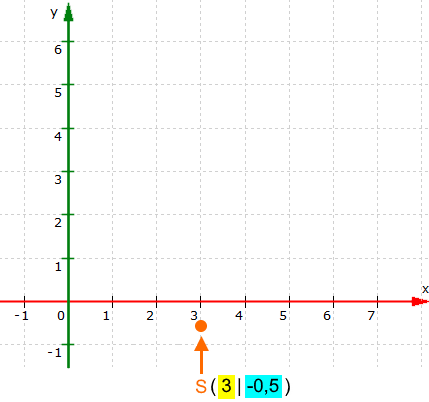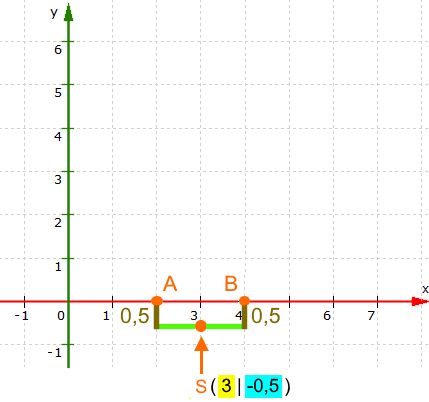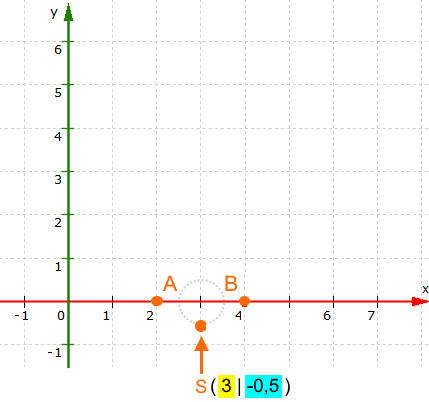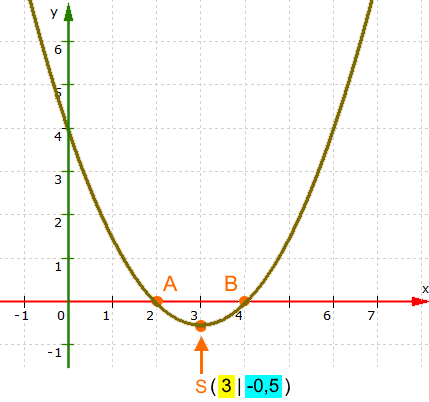
(Nebenbei:
Auf den irritierenden Umstand, dass
werden wir unten noch ausführlich zu sprechen kommen, ja, diese Irritation ist sogar das eigentliche Thema dieses Textes.)
Nun ist die Berechnung des Scheitel- bzw. Tiefpunkts S ( 3 | - 0,5 ) aber sehr umständlich - und hat noch andere Nachteile:
(wenn eine Funktion sie überhaupt hat)
überall im Koordinatensystem liegen, d.h. für ihre x- und y-Koordinaten gibt es keinerlei Systematik.
Nun lieben die Mathematiker aber systematische Vorgehensweisen, was im vorliegenden Fall bedeutet: Mathematiker wollen
(und Funktionen damit vergleichbar machen)
|
Solche „besonders geeigneten“ Punkte sind
|
(Kleiner Nachteil dieser Punkte: es gibt Funktionen,
Damit scheinen
gleichwertig zu sein - und ist erstmal unklar, weshalb im Mathematikunterricht
 .
.
Dafür gibt es zwei Gründe:
da Funktionen jedem x-Wert (hier x = 0) genau einen y-Wert zuordnen, können sie höchstens einen Schnittpunkt mit der y-Achse haben, aber durchaus mehrere Schnittpunkte mit der x-Achse (also mehrere Nullstellen):
 ;
;
nehmen wir z.B. nochmals die Funktion f mit der Funktionsgleichung y = 0,5x2 - 3x + 4.
Beim Schnittpunkt mit der y-Achse ist die x-Koordinate gleich 0 , also Sy ( 0 | ? ). Wenn wir nun für die x in der Funktionsgleichung jeweils 0 einsetzen, folgt:
y = 0,5 • 0 2 - 3 • 0 + 4 =
= 0,5 • 0 - 3 • 0 + 4 =
= 0 - 0 + 4 = 4
oder kurz y = 4 und somit Sy ( 0 | 4 ).
Wir hätten also überhaupt nicht rechnen müssen, sondern die 4 ganz hinten in y = 0,5x2 - 3x + 4 ablesen können.
hier ist y = 0 und somit N ( ? | 0), womit sich z.B. im Fall y = 0,5x2 - 3x + 4 ergibt:
0 = 0,5x2 - 3x + 4 ,
und das ist (nach Normierung) nur mittels
quadratischer Ergänzung bzw. der Formel
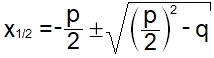 , also mit
erheblicher Rechnerei lösbar
, also mit
erheblicher Rechnerei lösbar
(und ergibt die Nullstellen A = N1 ( 2 | 0 ) und B = N2 ( 4 | 0 ) ).
Die Rechnungen sind aber so schwierig, weil in 0 = 0,5x2 - 3x + 4 das x sowohl quadratisch als auch einfach vorkommt.
Aber in diesem Text geht es mir gar nicht um Rechnungen, sondern um ein tieferes Verständnis von Schnittpunkten von Funktionsgraphen mit der x- und der y-Achse.
Rein innermathematisch haben die Punkte N1, N2 und Sy auf der x- bzw. y-Achse etwa in
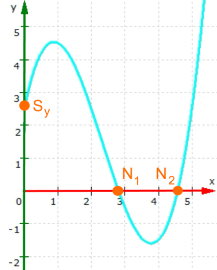
keine andere Bedeutung als eben die, dass sie auf der x- bzw. y-Achse liegen
(und deshalb eine ihrer beiden Koordinaten 0 ist, weshalb sich relativ einfach mit ihnen rechnen lässt).
Genauso gut könnte man auch jene Punkte betrachten, die auf dem Rand eines Smileys liegen
(wobei die Rechnungen allerdings ein bisschen schwieriger ausfallen würden).
Dabei wäre es - rein innermathematisch gesehen - völlig uninteressant, dass der Smiley lächelt: zur Berechnung der orangen Punkte würde allein der Außenkreis des Smileys interessieren:
Die Mathematik kann einem also jeden Spaß verderben:

Dass die Punkte N1, N2 und Sy in

auf der x- bzw.
y-Achse liegen, ist etwa so (un-)interessant
wie 
 .
.
Eine Bedeutung
in dem Sinne, dass etwas Anderes gemeint ist,
in dem Sinne, dass etwas wichtig ist,
gewinnen die Schnittpunkte mit der x- bzw. y-Achse aber überhaupt erst, wenn die Mathematik auf außermathematische Sachverhalte angewandt wird, also z.B.
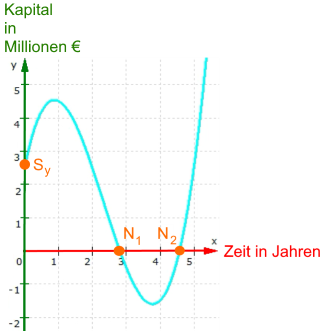
Die Grafik soll das Kapital einer frisch gegründeten Firma (neudeutsch: eines start-ups) im Laufe der Jahre darstellen:
Sy zeigt das Anfangskapital von ca. 2,6 Millionen € an
(das der Firmengründer von Mama und Papa geschenkt bekommen hat).
Anfangs steigt das Kapital noch, macht die Firma also (zusätzliche) Gewinne,
Nach ca. einem Jahr ist aber erste (lokale) Maximum erreicht, nach dem das Kapital abnimmt,
und in N1 , also nach ca. 2,8 Jahren, ist es völlig aufgezehrt, der Betrieb also pleite
(Tränen über Tränen: der Filius hat "mal eben" schlappe 2,6 Millionen € verbrannt).
Weil Mama und Papa gegenüber ihrem verwöhnten Sohnemann inzwischen vorsichtiger geworden sind und ihm nur noch einen (wenn auch zinslosen) Kredit geben, berappelt der Betrieb sich aber langsam wieder
und kommt er in N2 dann doch wieder in die Gewinnzone
(oh welche Erleichterung!).
Schüler haben selten Schwierigkeiten damit,
die Koordinaten eines im Koordinatensystems vorgegebenen Punkts abzulesen, also z.B.
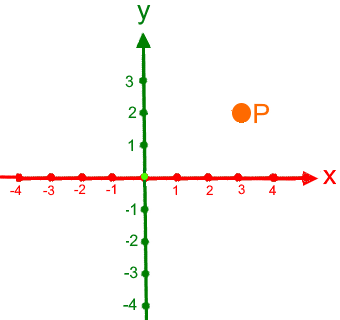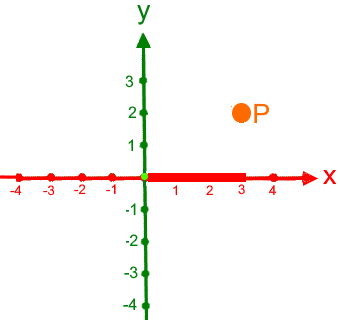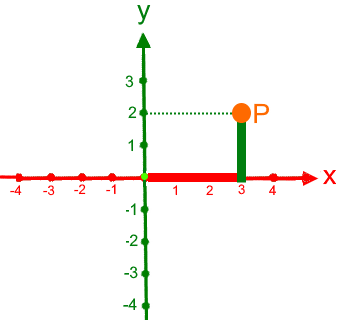
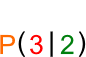
oder umgekehrt mit den vorgegebenen Koordinaten einen Punkt ins Koordinatensystem einzuzeichnen, also z.B.
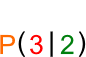

 .
.
Aber das fällt vielen Schülern nur so lange leicht, wie die Punkte NICHT auf den Koordinatenachsen liegen.
Wenn man sie aber bittet, zu einer vorgegebenen Funktion den Schnittpunkt Sy mit der y-Achse und die Schnittpunkte mit der x-Achse (Nullstellen) zu berechnen, stehen sie oft auf dem Schlauch:
entweder wissen sie überhaupt keinen Ansatz (dass eine der beiden Punktkoordinaten 0 ist),
oder sie wissen nicht, welche der beiden Punktkoordinaten 0 ist,
oder sie setzen die falsche Punktkoordinate gleich 0 .
Damit sind wir endlich beim eigentlichen, oben bereits kurz angedeuteten Thema dieses Aufsatzes, nämlich beim
"[...] irritierenden Umstand, dass
Fragt sich nur, warum viele Schüler so (scheinbar) blöd sind:

Dafür scheint es mir mehrere Gründe zu geben:
und vermutlich am wichtigsten: das Koordinatensystem ist nicht gründlich genug durchgenommen worden.
 vorausgesetzt statt mal gründlich auf seine Raffinesse hin
untersucht;
vorausgesetzt statt mal gründlich auf seine Raffinesse hin
untersucht;(hier leider nur einige Zwischenzustände statt kontinuierlicher Bewegungen):
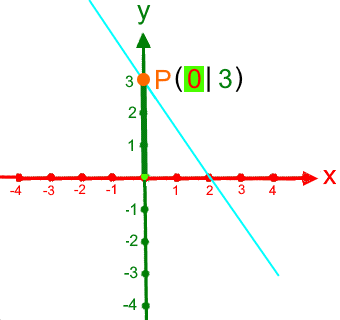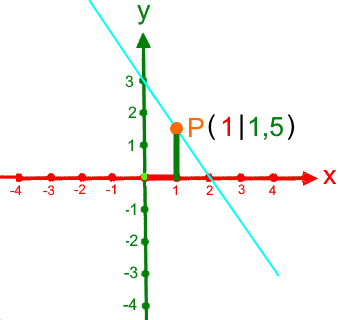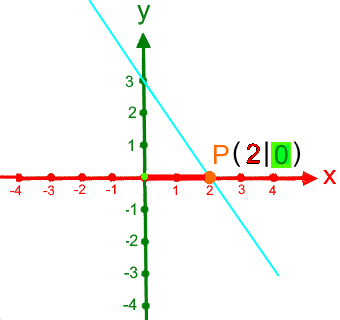 .
.
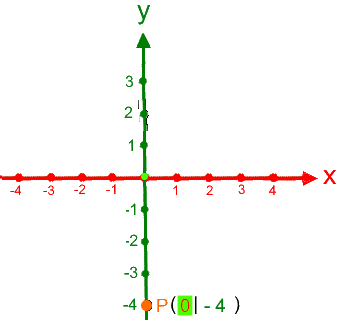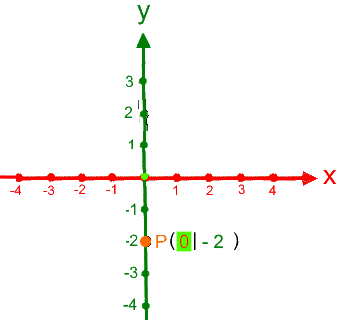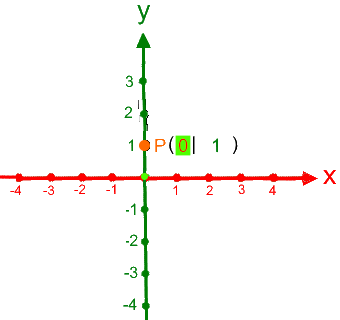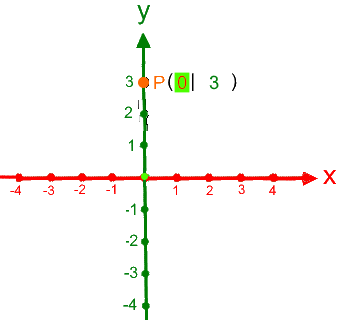
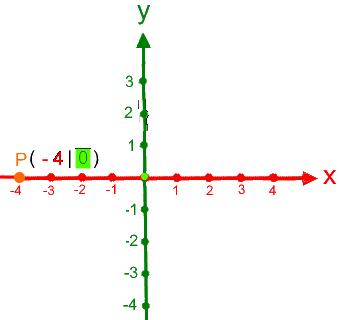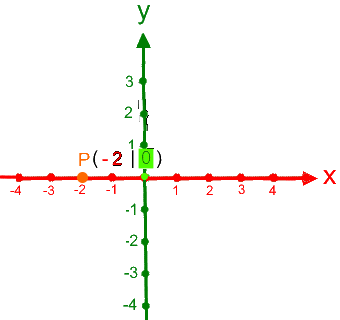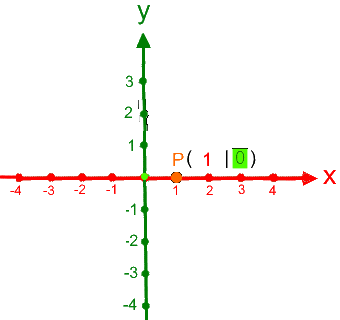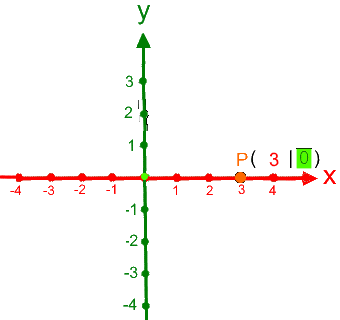
 durchgenommen
werden,
durchgenommen
werden,
wird all das irgendwann mal frisch erworbene Wissen später immer vorausgesetzt statt immer wieder aufs Neue durchgenommen.
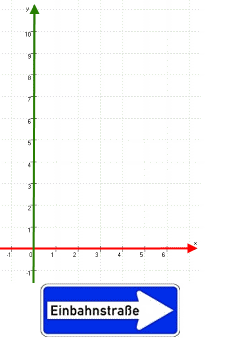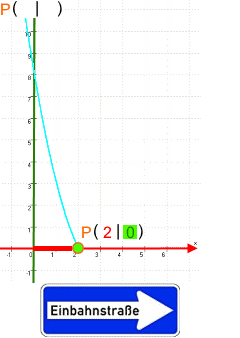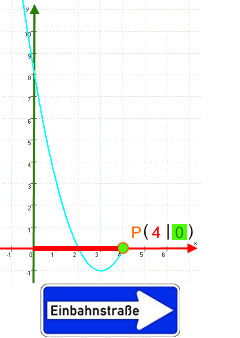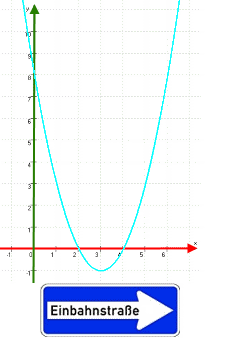
beherrschen die Schüler den exemplarischen Fall
 , weil sie da
die x- und y-Koordinate
TUN, also
, weil sie da
die x- und y-Koordinate
TUN, also
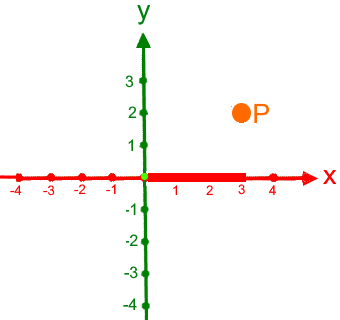 , also entlang
der x-Achse,
, also entlang
der x-Achse,
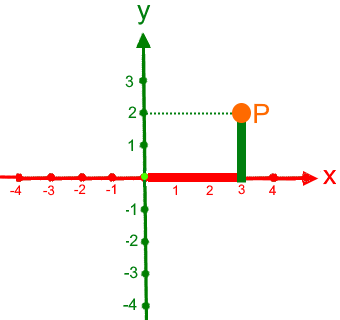 , also parallel
zur y-Achse.
, also parallel
zur y-Achse.
Hingegen gibt es
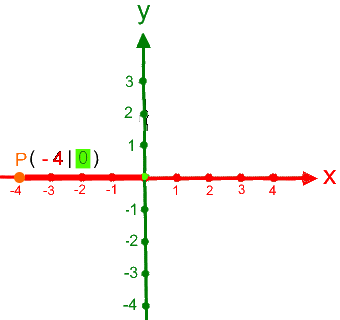 nur eine (!)
Bewegung auf der x-Achse (aber keine auf der y-Achse),
nur eine (!)
Bewegung auf der x-Achse (aber keine auf der y-Achse),
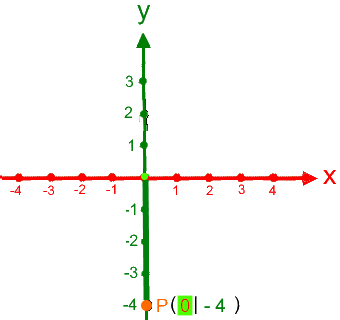 nur
eine (!) Bewegung auf der y-Achse (aber keine auf der x-Achse),
nur
eine (!) Bewegung auf der y-Achse (aber keine auf der x-Achse),d.h. die jeweils andere 0-Koordinate entsteht (?) durch ein Nichts-TUN.
("null" und "nichts" sind für Schüler bekanntermaßen schwer miteinander vereinbare oder schwer zu unterscheidende Begriffe: "bei der Gleichungslösung kommt nix raus" kann dann fallweise bedeuten
Entsprechend ist
 die
y-Koordinate UNSICHTBAR,
die
y-Koordinate UNSICHTBAR,
 die
x-Koordinate UNSICHTBAR.
die
x-Koordinate UNSICHTBAR.Was aber weder GETAN
wird noch SICHTBAR ist, bleibt abstrakt:

Ein anderer Zugang:
das zwei dimensionale
(kartesische) Koordinatensystem
dimensionale
(kartesische) Koordinatensystem
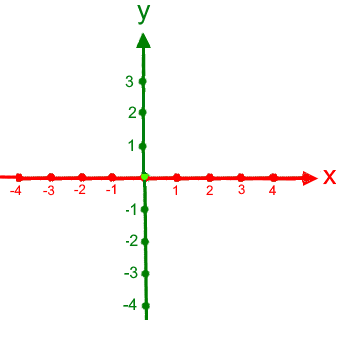 :
:
(jedem x-Wert wird genau ein y-Wert zugeordnet),
also reicht für die Graphen dieser Funktionen das zweidimensionale Koordinatensystem.
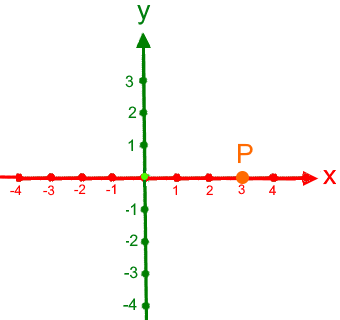
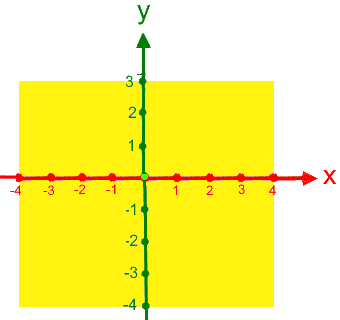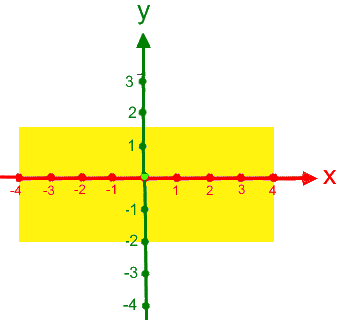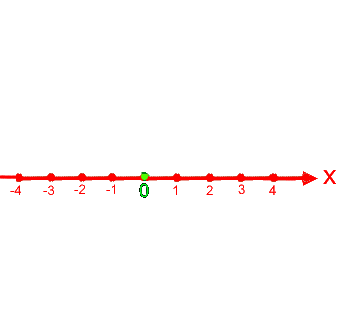
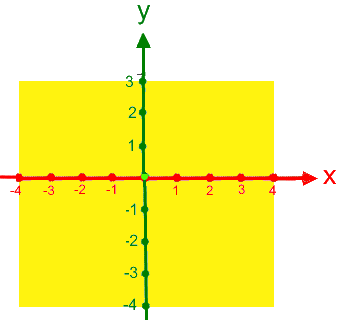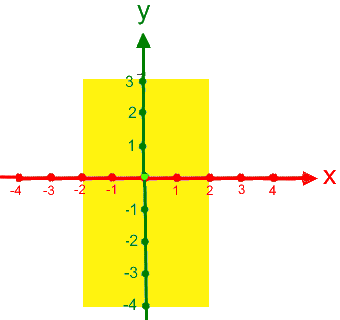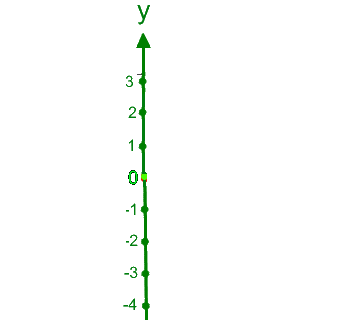
Da P auf der x-Achse liegt, brauchen wir die y-Achse eigentlich gar nicht:

Rückübersetzt ins zweidimensionale Koordinatensystem:
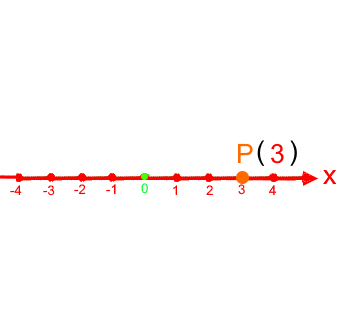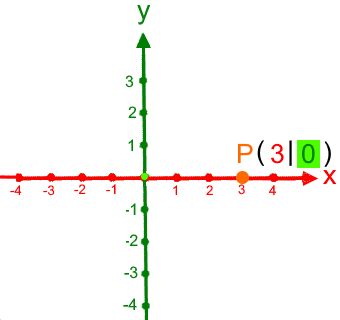
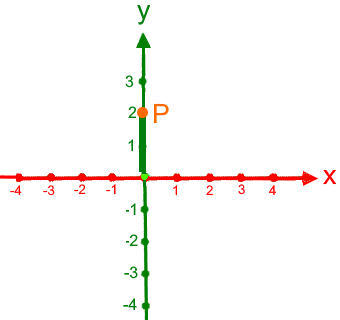
Da P auf der y-Achse liegt, brauchen wir die x-Achse eigentlich gar nicht:
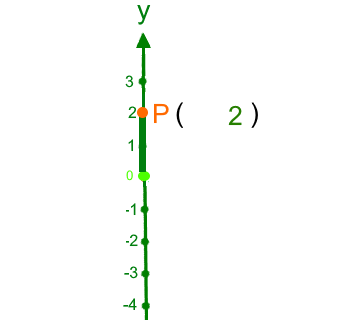
Rückübersetzt ins zweidimensionale Koordinatensystem:
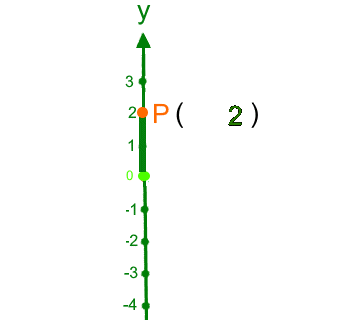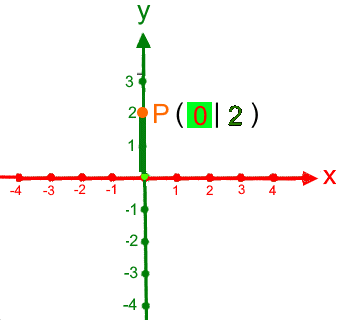
Wir hatten oben gesehen, dass das Rechnen mit 0 besonders einfach ist
(wenn man mal von der verbotenen Division durch 0 absieht):
3 + 0 = 3 4 + 0 = 4
3 - 0 = 3 4 - 0 = 4
3 • 0 =
0
4 • 0 = 0
 (die ausgleichende
Gerechtigkeit), wenn mit ihr multipliziert wird:
(die ausgleichende
Gerechtigkeit), wenn mit ihr multipliziert wird:
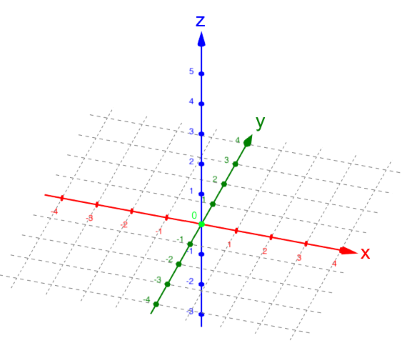
das drei dimensionale
(kartesische) Koordinatensystem
dimensionale
(kartesische) Koordinatensystem
 :
:
Um ein dreidimensionales Koordinatensystem zu erhalten,
 aus und fügen
diesem eine dritte, nämlich die z-Achse
hinzu,
aus und fügen
diesem eine dritte, nämlich die z-Achse
hinzu,Wenn wir uns das zweidimensionale Koordinatensystem so vorstellen, dass es wie in einem Schulheft auf einem Schreibtisch liegt, so kann das nur bedeuten, dass die z-Achse
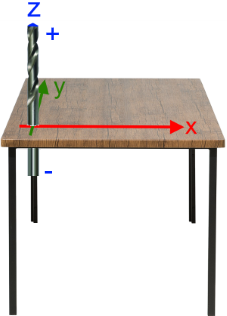
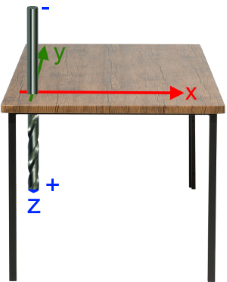 .
.
Wir wählen
 , weil es einfacher
ist, mit positiven Zahlen zu rechnen und wir diese gerne oberhalb
der Tischplatte haben.
, weil es einfacher
ist, mit positiven Zahlen zu rechnen und wir diese gerne oberhalb
der Tischplatte haben.
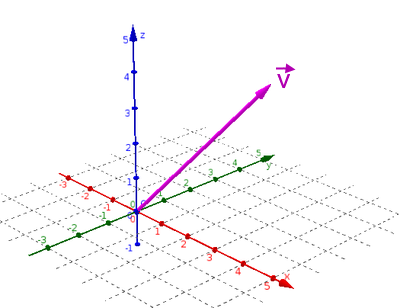
Nun ergibt sich allerdings ein Problem, wenn wir von oben auf den Schreibtisch herabsehen: die neue z-Achse kommt direkt auf unser Auge zu, d.h. für uns sieht die Achse aus wie ein Punkt im zweidimensionalen Koordinatensystem
(vgl. einen Pfeil
 , der direkt auf
uns zukommt
, der direkt auf
uns zukommt  ):
):
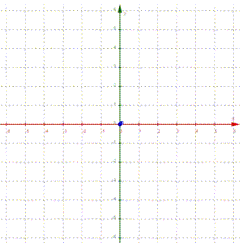
Erst wenn wir dieses Koordinatensystem
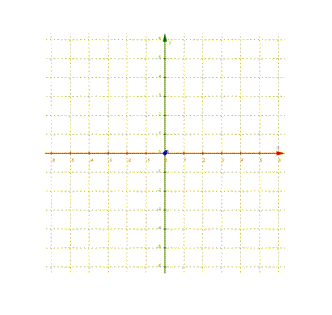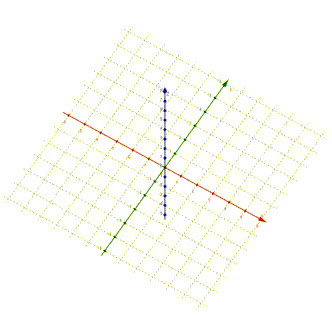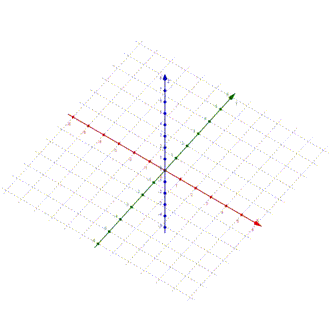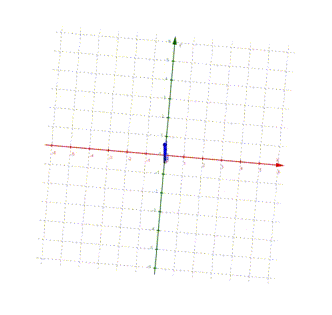
Aber nochmal kurz zur Sicht von oben: unsere Konstruktion des dreidimensionalen Koordinatensystems hat den Vorteil, dass
 sichtbar bleibt
sichtbar bleibt
Um sich die Richtungen der Achsen zu merken, gibt es eine schöne "Faustregel", nämlich die "Rechte[!]-Hand-Regel":
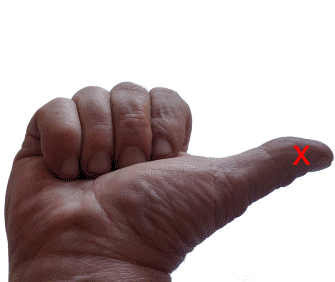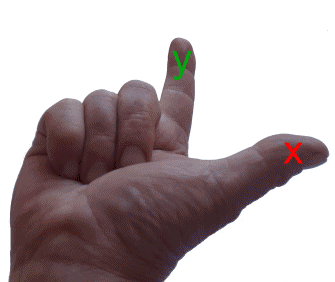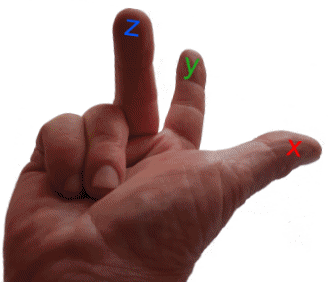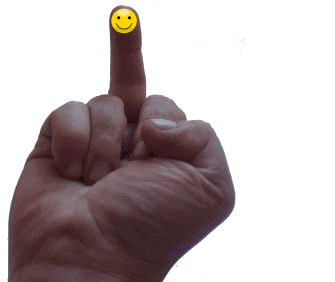
(Vgl. die "Rechte-Hand-Regel" in der Physik:
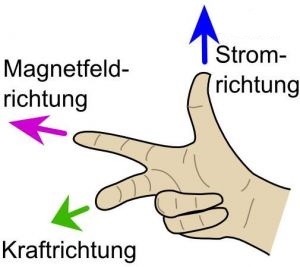 )
)
Wem die Computeranimation
 zu abstrakt ist
zu abstrakt ist
(denn sie ist ja doch wieder nur die zweidimensionale Projektion von etwas Dreidimensionalem),
der baue sich mal schnell dreidimensionale Modelle
(die ich hier aber auch wieder nur mit zweidimensionalen Fotos vorführen kann):
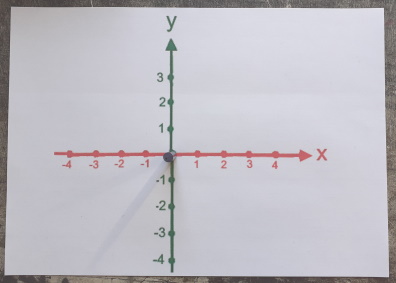 ↔
↔
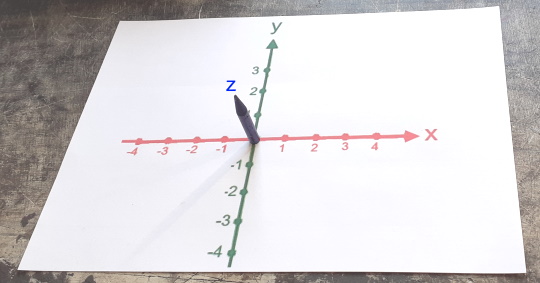 ,
,
 ,
,
 hilfreich,
hilfreich,

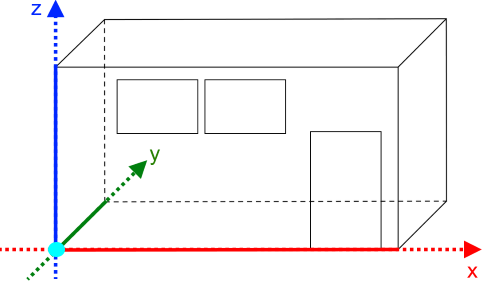
(Vgl. auch
![]()
 ; Foto während einer Klassenarbeit entstanden: die Ebenen und Geraden hatte ich
selbst vorher gespannt.)
; Foto während einer Klassenarbeit entstanden: die Ebenen und Geraden hatte ich
selbst vorher gespannt.)
Echte dreidimensionale Modelle haben allerdings einen entscheidenden Nachteil: es ist schwierig, in diesen Modellen Punkte zu markieren, wenn diese nicht in der xy- oder xz- oder yz-Ebene (s.u.), sondern "in der Luft hängen".
(Ich werde demnächst aber mal versuchen, ein dreidimensionales Modell zu entwickeln, in dem das möglich ist.)
Deshalb arbeitet man dann eben doch meistens mit zweidimensionalen Zeichnungen (Projektionen) dreidimensionaler Koordinatensysteme, also z.B.
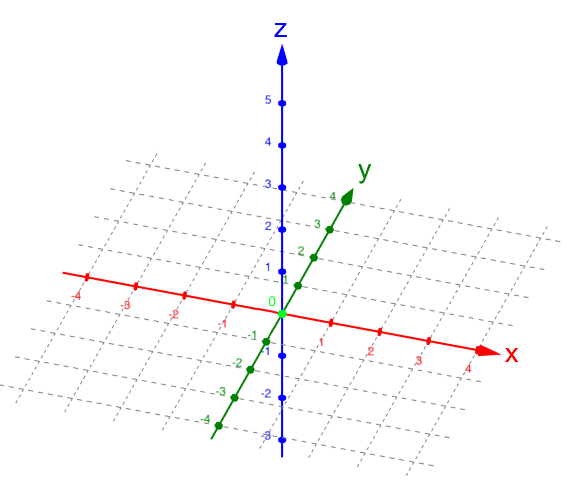 .
.
Da kann man zwar relativ einfach vorgegebene Punkte eintragen, nämlich z.B. P ( 2 | 3 | 4 ) :
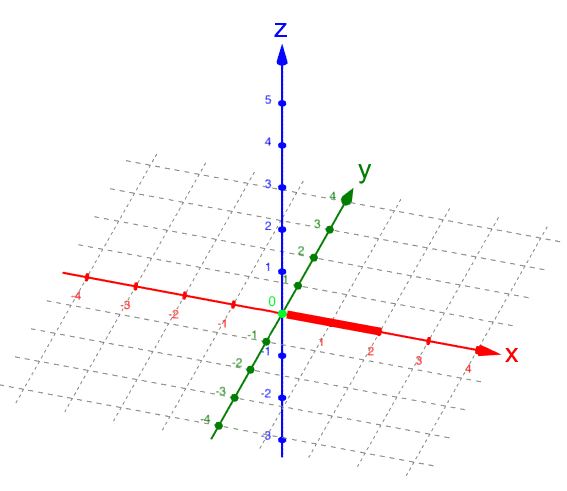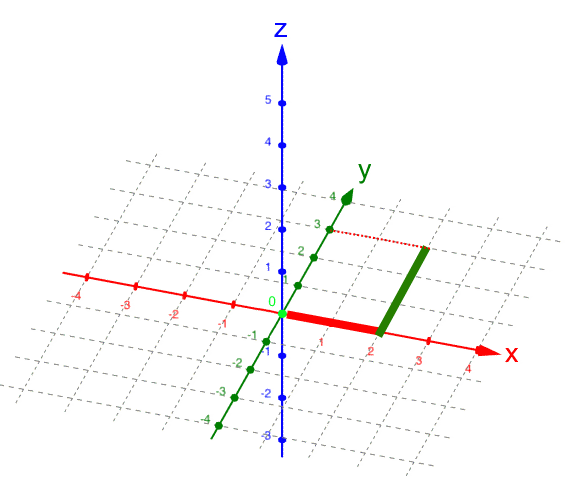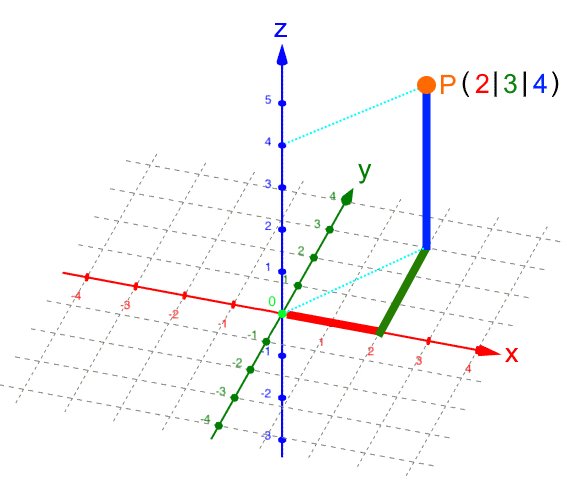
Man kann aber nicht (eindeutig) von einem im Koordinatensystem vorgegebenen Punkt dessen Koordinaten ablesen. Ein Beispiel ist da
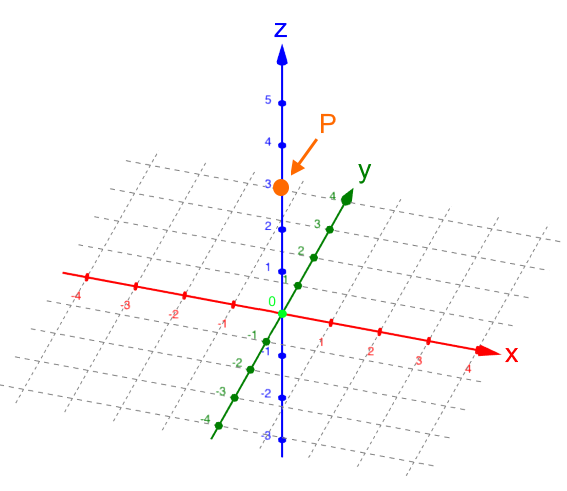
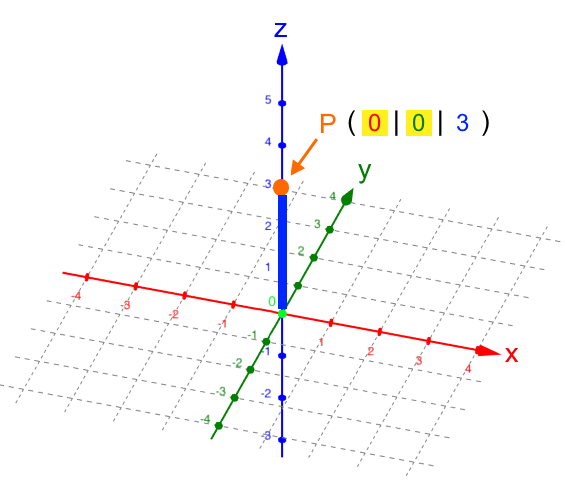
Genauso sind aber auch möglich:
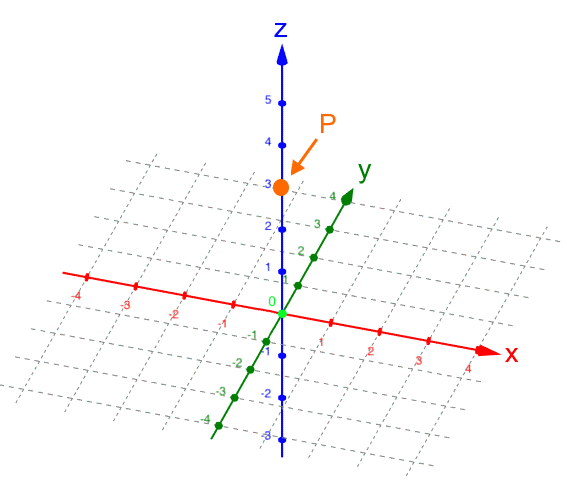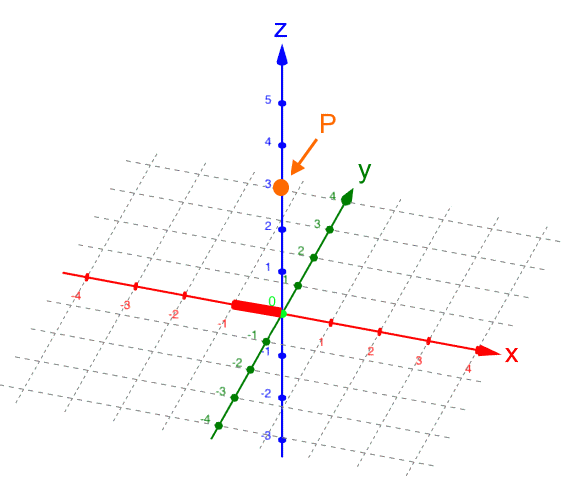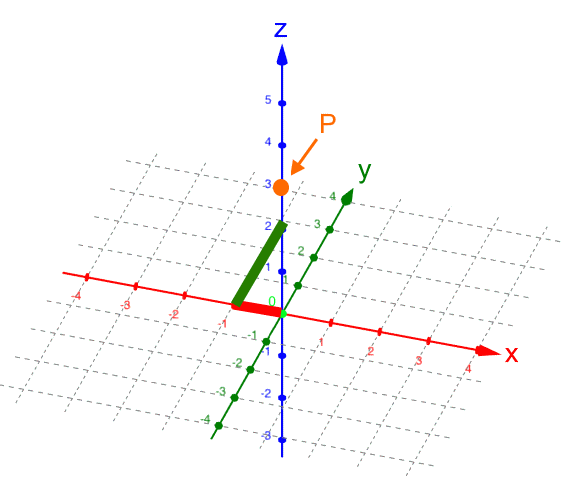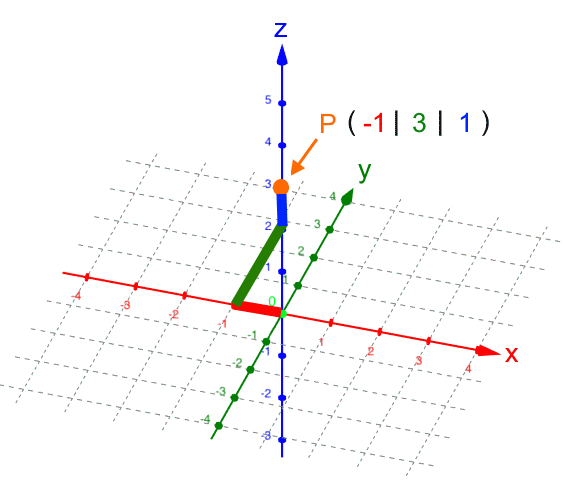 , d.h.
P liegt aus unserem Blickwinkel gesehen
hinter der z-Achse;
, d.h.
P liegt aus unserem Blickwinkel gesehen
hinter der z-Achse;
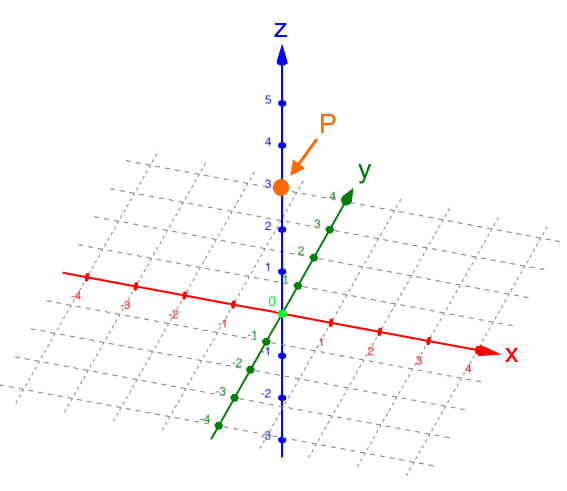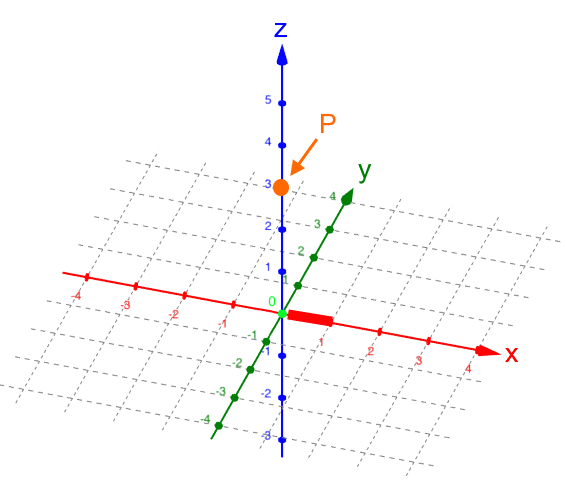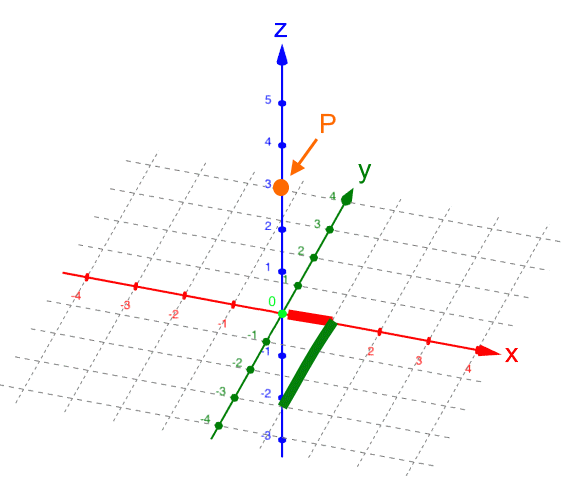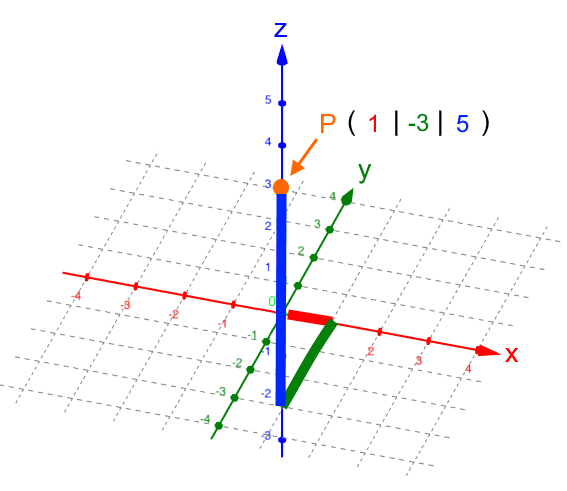 , d.h.
P liegt aus unserem Blickwinkel gesehen
vor der z-Achse.
, d.h.
P liegt aus unserem Blickwinkel gesehen
vor der z-Achse.
Mit P können also alle (unendlich viele) Punkte gemeint sein, die auf einer Geraden liegen, die von unserem Auge durch P geht
(bzw. P ist eine von hinten gesehene Gerade).
Dass drei unterschiedliche Punkte identisch aussehen, zeigt schon: die zweidimensionale Projektion des dreidimensionalen Koordinatensystems ist nicht „längentreu“, denn
Kurz gesagt: man kann aus der zweidimensionalen Projektion oftmals nicht reale Entfernungen ablesen.
Und genauso ist die zweidimensionale Projektion nicht „winkeltreu“. Z.B.
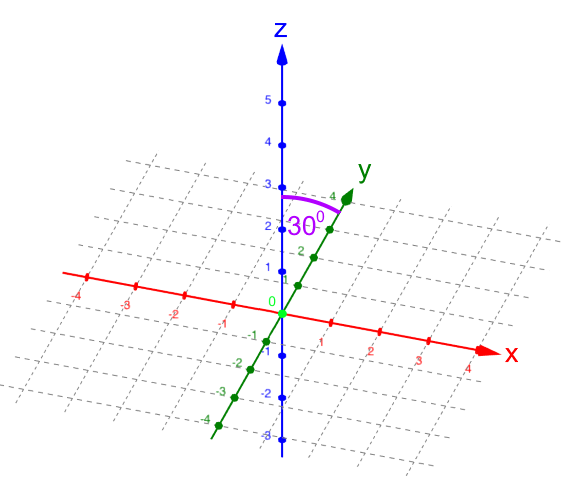 ,
,Kurz gesagt: man kann aus der zweidimensionalen Projektion oftmals nicht reale Winkel im Dreidimensionalen ablesen.
Die zweidimensionale Projektion des dreidimensionalen Koordinatensystems hat also fast nur schwerwiegende Nachteile. Um so dringlicher wäre also eigentlich ein dreidimensionales Modell. Und der Rest ist notgedrungen unanschauliches Rechnen.
Halten wir noch kurz fest:
 ,
,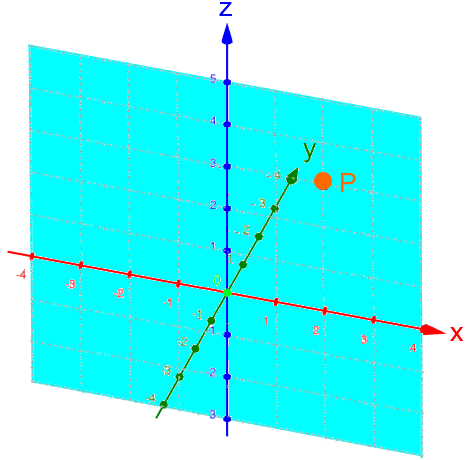 ,
,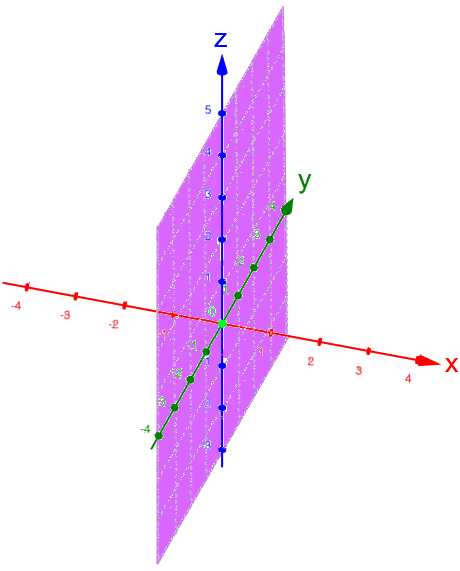 :
:
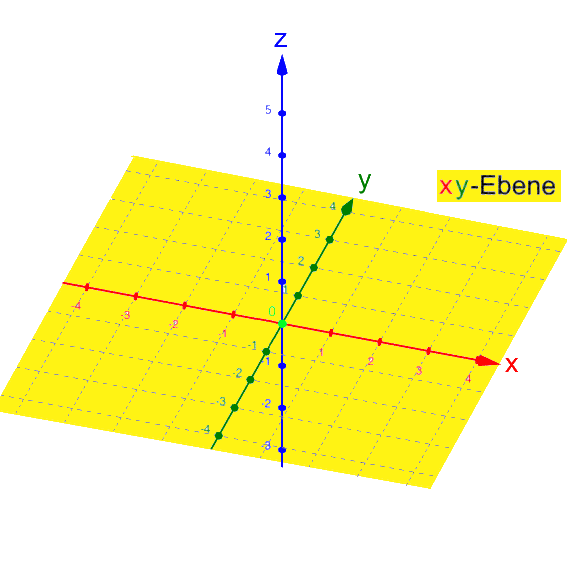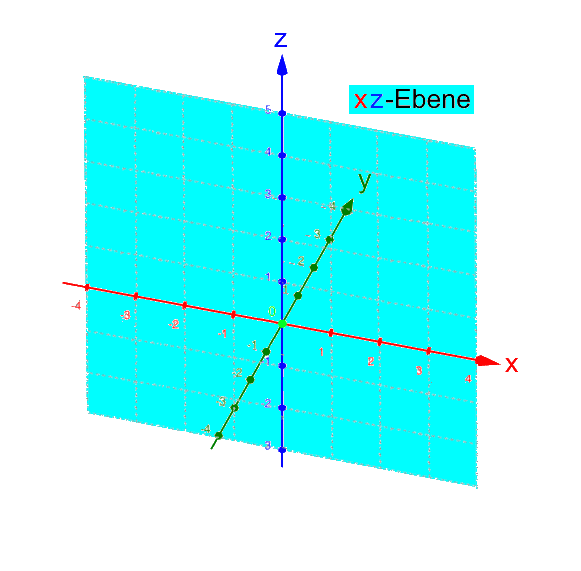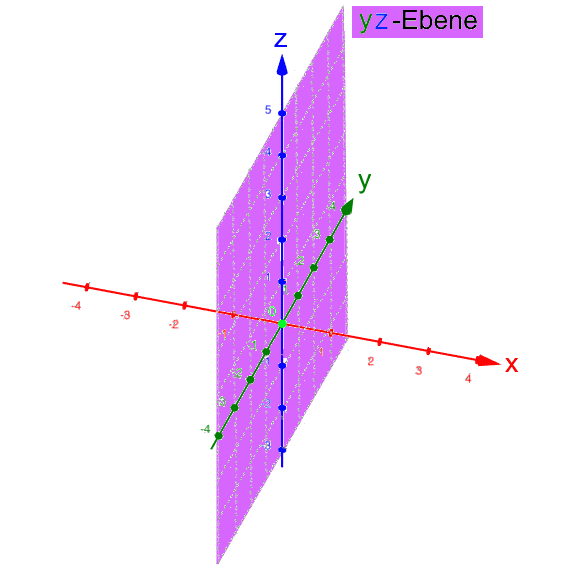
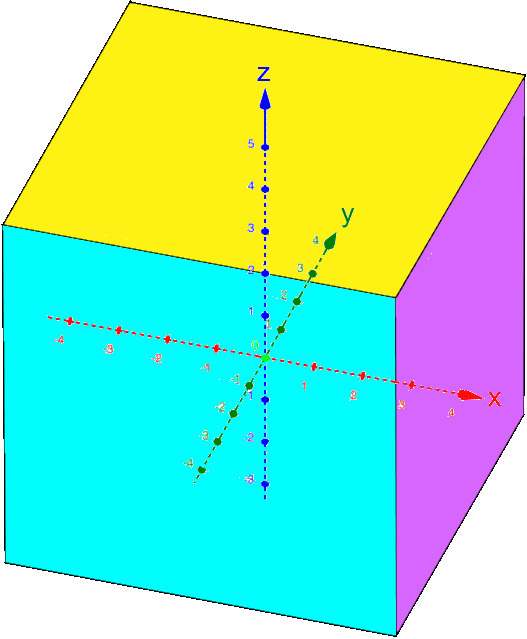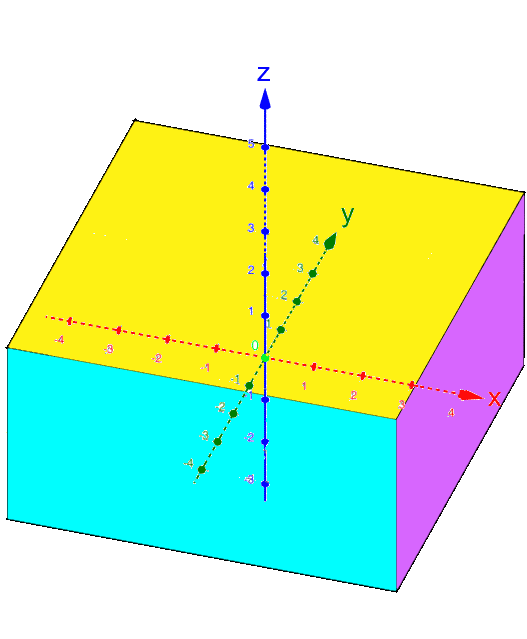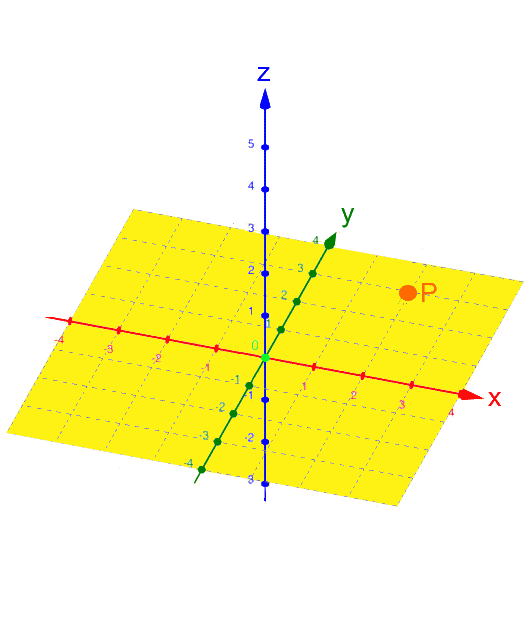
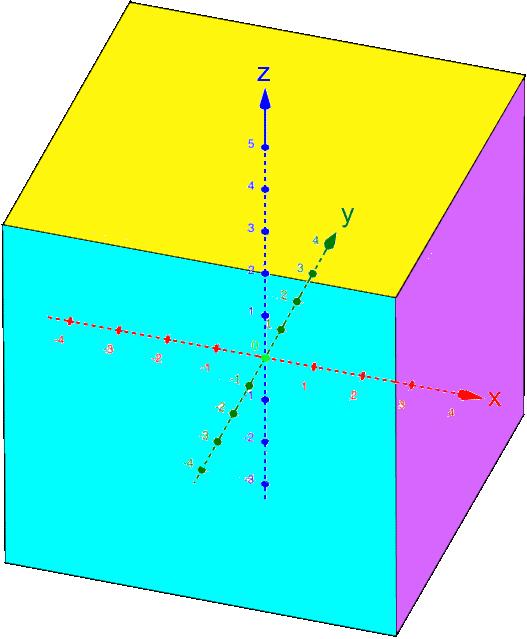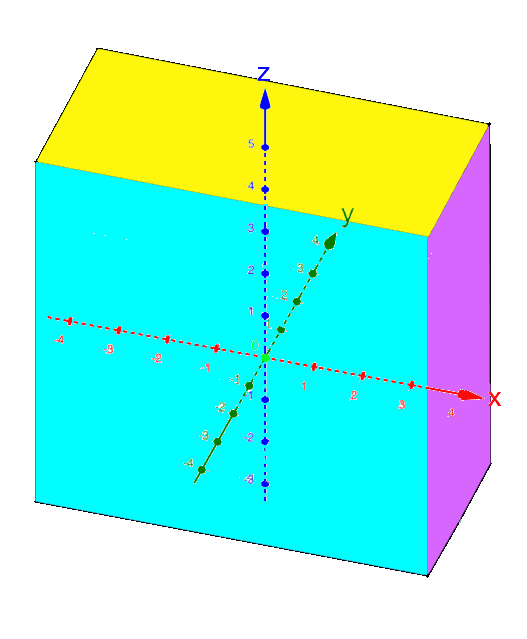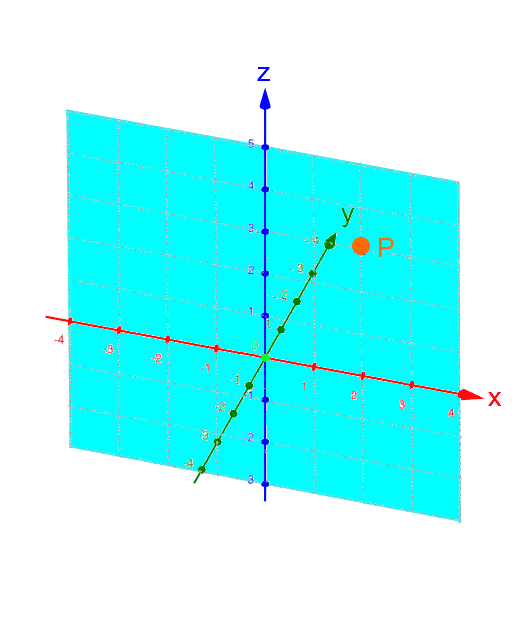
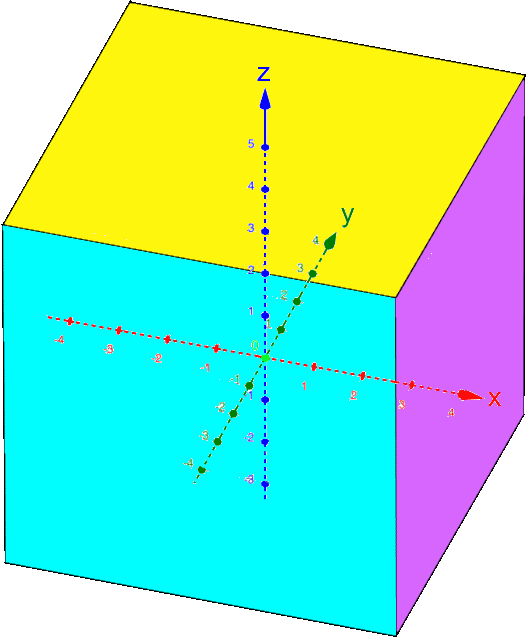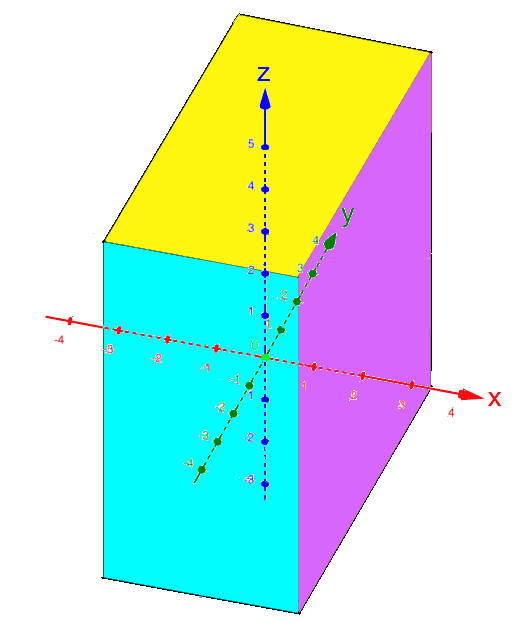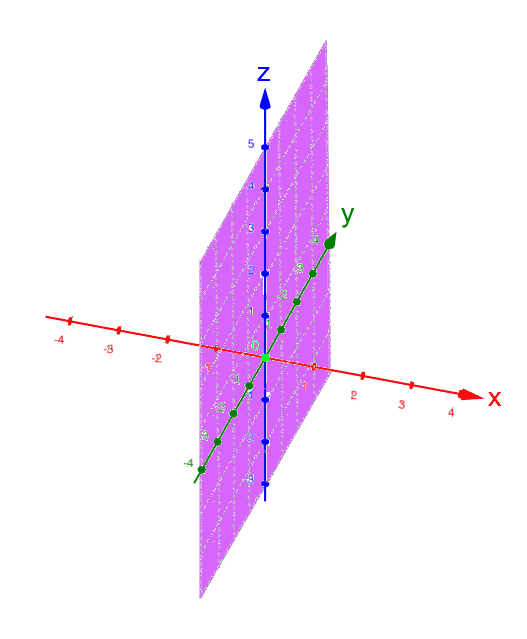
Ebenfalls noch kurz sei festgehalten, dass oftmals
genannt wird. Grund dafür ist vermutlich, dass damit im vierdimensionalen Koordinatensystem
(das aber sowieso nicht mehr gezeichnet werden kann)
auch eine x4-Achse möglich wird
(während das Alphabet nach dem Buchstaben z zu Ende ist).
Solche vierdimensionalen Koordinatensysteme braucht man beispielsweise in der Relativitätstheorie, wo auf der x4-Achse zusätzlich noch die Zeit eines Ereignisses notiert wird.
(Vgl.: bei einem Fußballspiel ist es nicht nur wichtig, wo der Ball im dreidimensionalen Raum ist, sondern auch, wann er dort ist, nämlich während der Spielzeit.)
In der Schule spielen solche vierdimensionalen Koordinatensysteme aber keine Rolle, und deshalb scheint mir die Umbenennung der Achsen auch unnötig und für Schüler evtl. verwirrend.
Oftmals werden die Koordinatenachsen dann auch anders angeordnet:
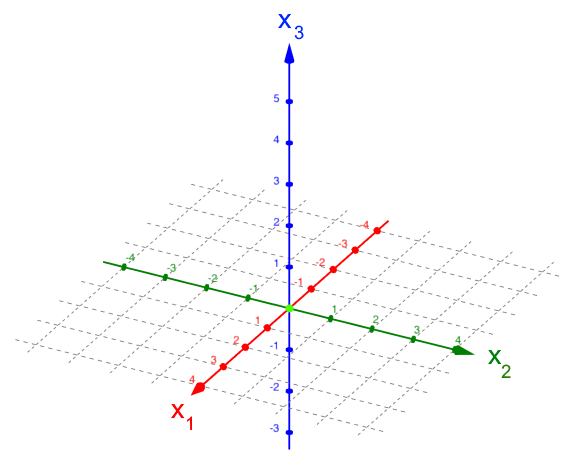
Ich mag diese neuen Richtungen nicht, weil damit die xy- bzw. x1x2-Ebene von oben gesehen zur eventuellen Verwirrung der Schüler
nicht mehr (wie im
Zweidimensionalen üblich) so 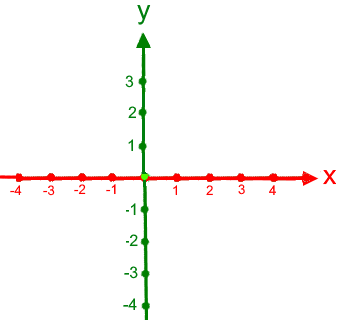 ,
,
sondern so 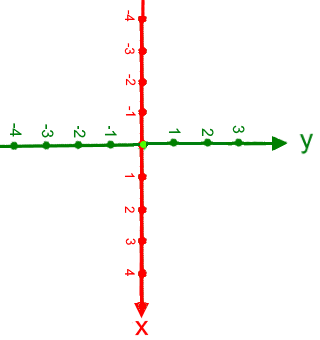 liegt.
liegt.
Hauptanwendungsgebiet von Koordinatensystemen sind Funktionen. Nun sind aber sämtliche in der Schule durchgenommenen Funktionen zweidimensional, ist so gesehen also gar kein dreidimensionales Koordinatensystem nötig.
Dennoch mal Beispiele für dreidimensionale Funktionen, bei denen aber
zugeordnet wird, so dass über/unter jedem Punkt der xy-Ebene immer nur ein Punkt des dreidimensionalen Funktionsgraphen liegt:
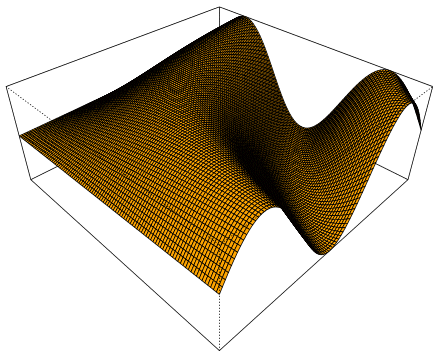
Da ist ein Funktionsgraph tatsächlich endlich mal schön, und schön ist erst recht die Bewegung, die sich durch eine Funktionenschar
(viele aufeinander folgende Funktionsgraphen)
ergibt:
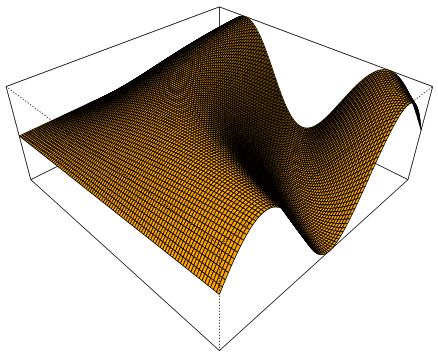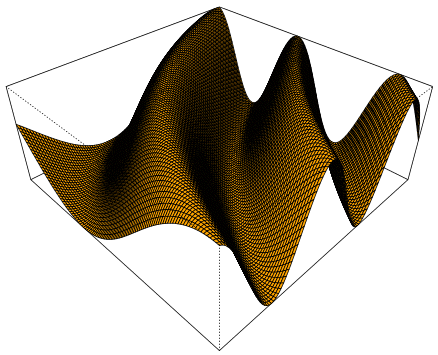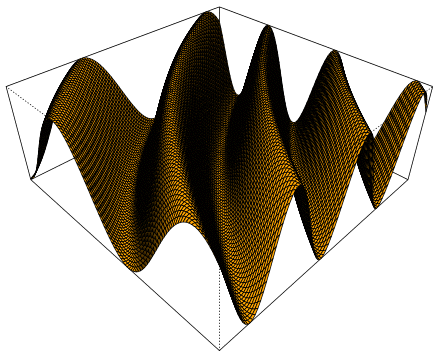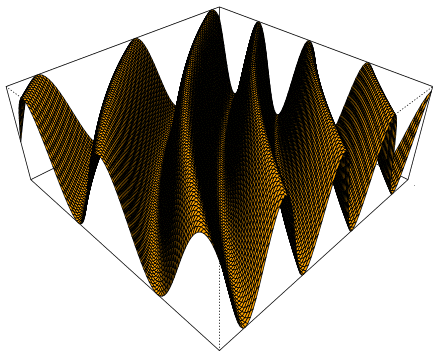
Das kann man sich auch so vorstellen, dass ein (Seiden-!)Tuch rechts immer schneller hoch und runter bewegt wird und diese Bewegungen sich in Raum und Zeit (!) ausbreiten (im Raum nach links):
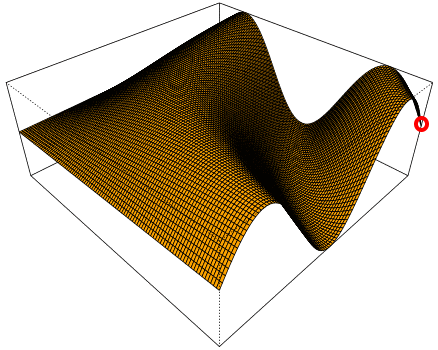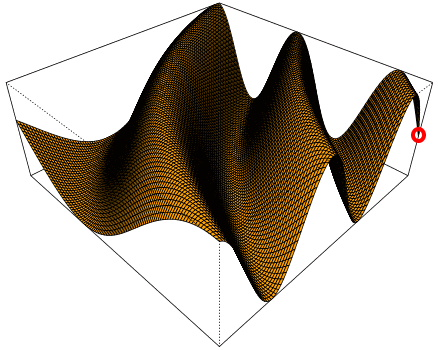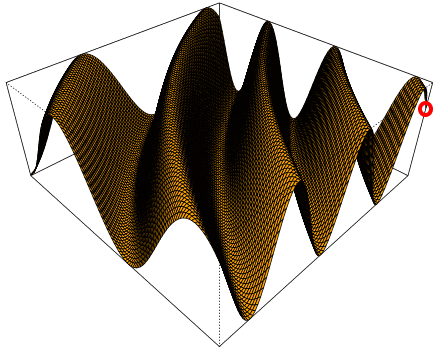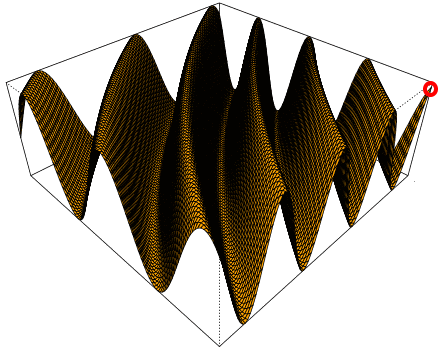
Da dreidimensionale Funktionen in der Schule allerdings nie vorkommen, bleibt dort "nur" ein anderes Anwendungsgebiet für das dreidimensionale Koordinatensystem, nämlich die Vektorgeometrie und da z.B.
 im
Dreidimensionalen (Raum):
im
Dreidimensionalen (Raum):
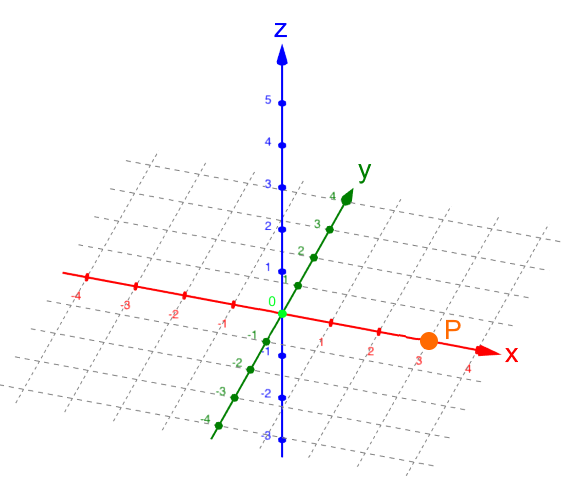
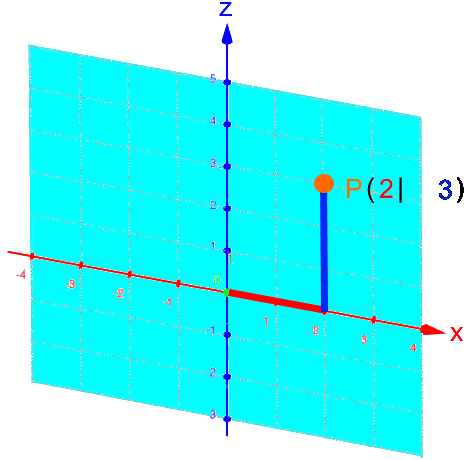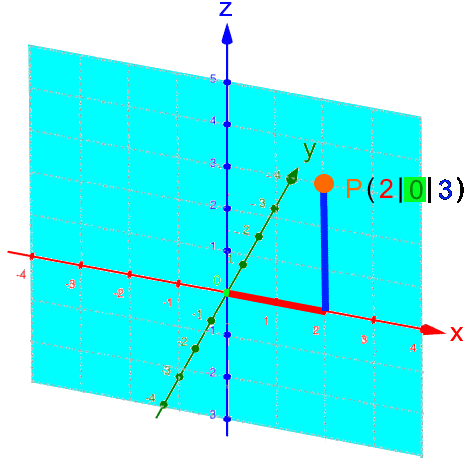
Da P auf der x-Achse liegt, brauchen wir die y- und die z-Achse eigentlich gar nicht:
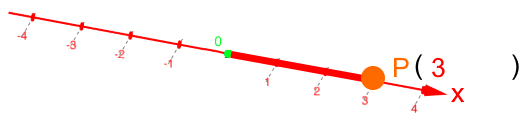
Rückübersetzt ins dreidimensionale Koordinatensystem:
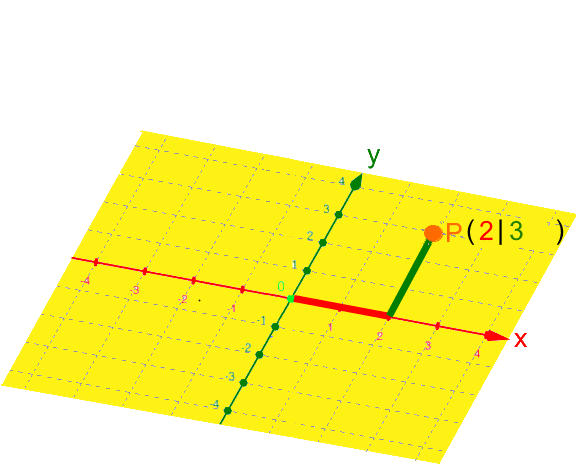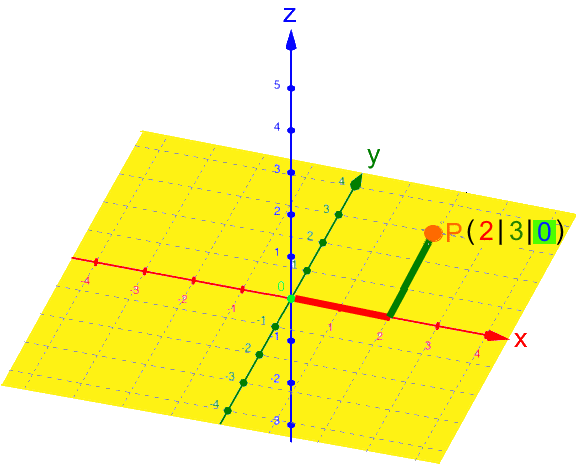
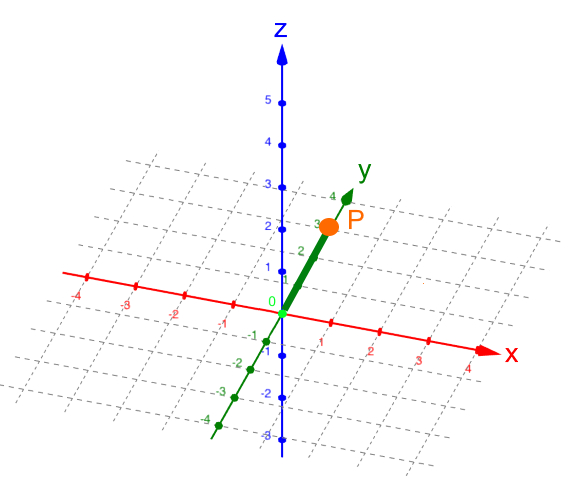
Da P auf der y-Achse liegt, brauchen wir die x- und die z-Achse eigentlich gar nicht:
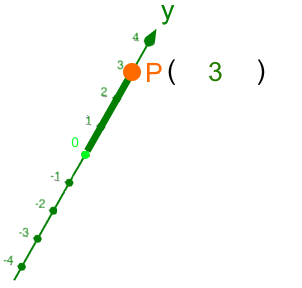
Rückübersetzt ins dreidimensionale Koordinatensystem:
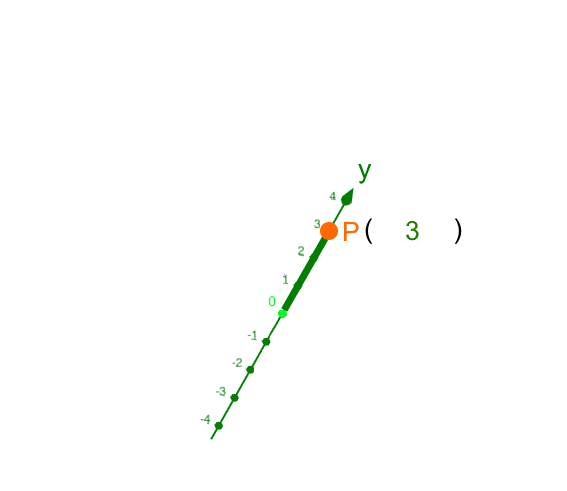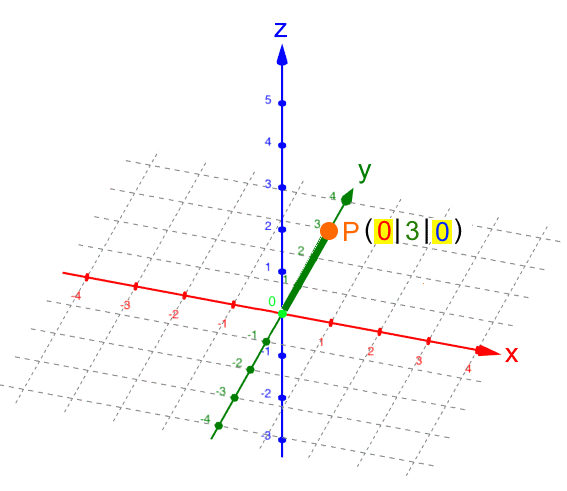
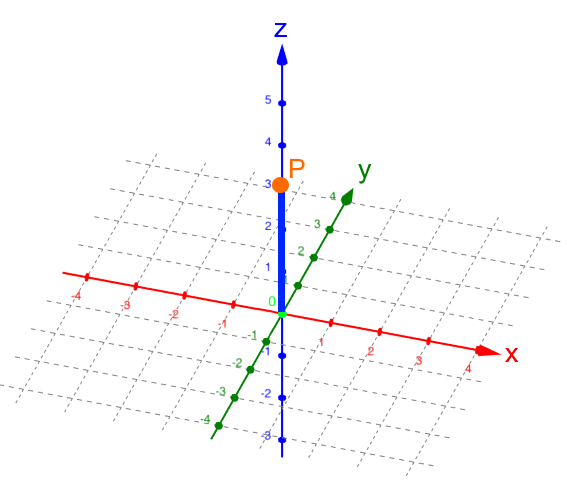
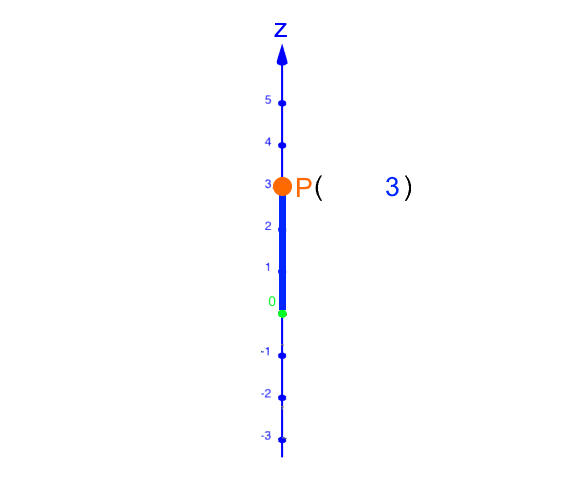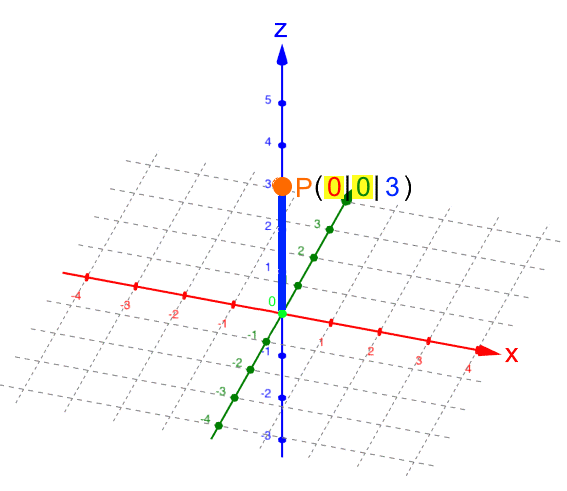
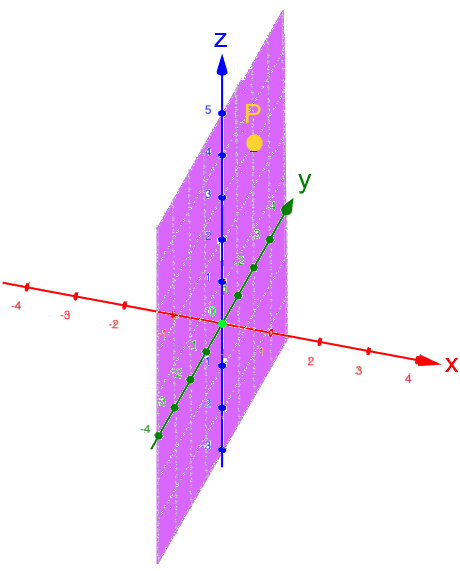
Da P auf der z-Achse liegt, brauchen wir die x- und die y-Achse eigentlich gar nicht:
.
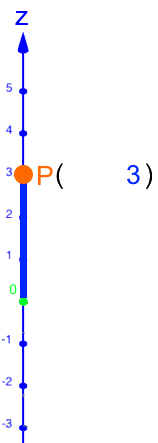
Rückübersetzt ins dreidimensionale Koordinatensystem:

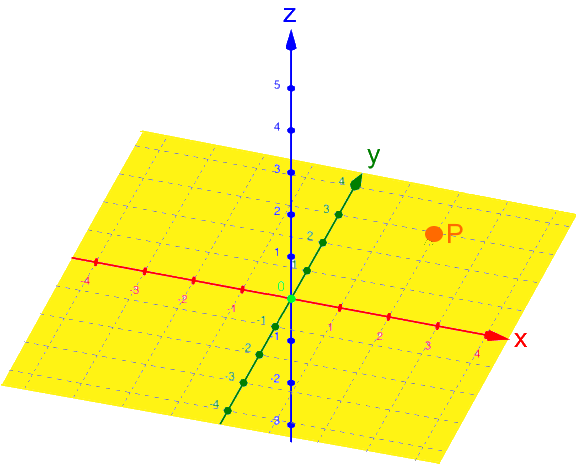
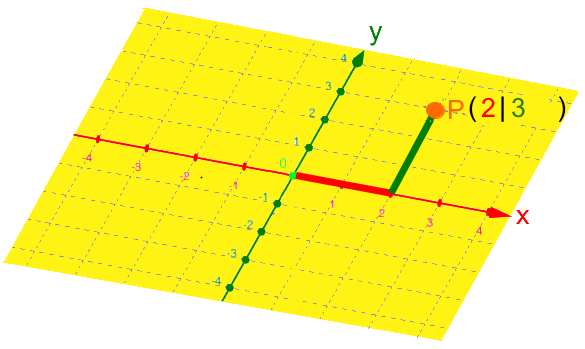
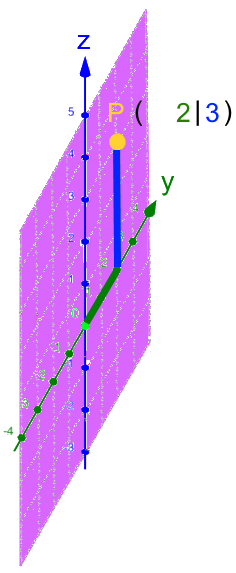
Da P in der xy-Ebene liegt, brauchen wir die xz- und die yz-Ebene eigentlich gar nicht:
. 
Rückübersetzt ins dreidimensionale Koordinatensystem:


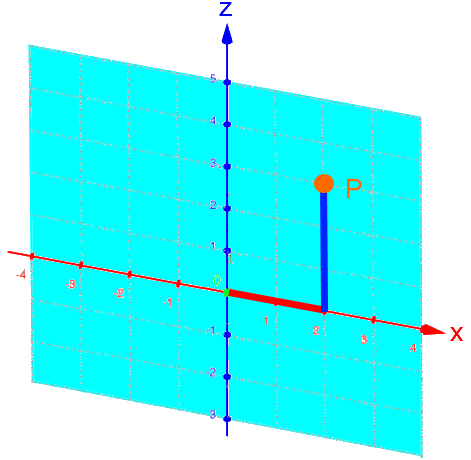
. .
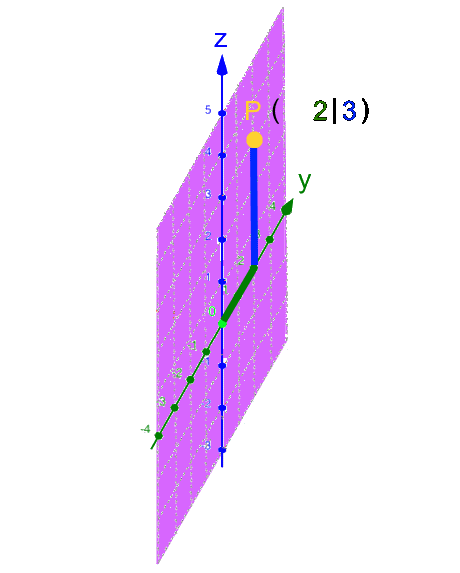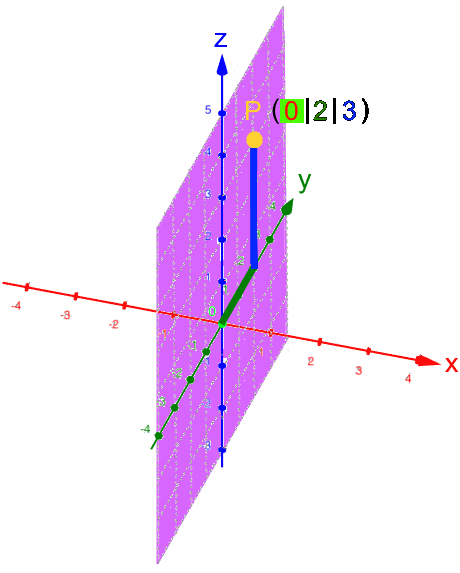

. .


Kurz zusammengefasst:

Aber wie soll man sich das alles merken??? - wenn man nicht ein (!) einfaches System dahinter entdeckt:
Es ist (sind)
immer die Koordinate(n) 0, die
links NICHT genannt wird (werden):
|
Schüler sollten sich eigentlich immer freuen, wenn der Lehrer so ausnehmend nett ist, in Aufgaben Punkte auf den Achsen bzw. in den von ihnen aufgespannten Ebenen vorzugeben, wird durch die Nullen das Rechnen
(vor allem mit sonst sehr mühsamen Gleichungssystemen)
doch erheblich einfacher.
Zuguterletzt sollte man auch die Umkehrung von

kennen (und üben), also
