
Beweisverfahren

Beweisverfahren
Beweise sind das Herz der Mathematik
(und überhaupt kann die Mathematik als einzige Wissenschaft hieb- und stichfeste Beweise führen, und das oftmals sogar für unendlich viele Fälle).
Da ist es doch schade, dass Beweise im heutigen Schulunterricht kaum mehr vorkommen
(schon gar nicht in einer übergeordneten Unterrichtseinheit "Beweisverfahren")
und den Schülern somit die eigentliche Mathematik vorenthalten wird.
Wann immer im Folgenden von Zahnradkonstellationen die Rede ist, sollte man Schüler zumindest anfangs mit echten, also z.B.

Lego®-Zahnrädern
hantieren lassen
Und am besten bauen die Schüler die unten gezeigten Konstellationen nicht einfach nur nach
(denn damit sind die wichtigsten Gesetze schon allzu suggestiv ausgewählt),
sondern probieren selbst verschiedene Kombinationen aus und entdecken dabei vielleicht auch Gesetze selbst
(evtl. wird man da als Lehrer vielleicht ein wenig nachhelfen müssen:
[evtl. gefolgt von dem Tipp, für das erste und letzte Zahnrad gleichgroße Zahnräder zu wählen, die sich dann leicht erkennbar gleichschnell drehen;
allerdings spielen die Aspekte c. und d. unten keine Rolle mehr;
und ebenfalls sei hier mal davon abgesehen, dass man Zahnräder auch
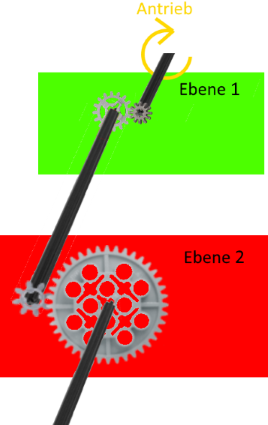 montieren kann, um die sich in d. zeigende Beschränkung aufzuheben,
montieren kann, um die sich in d. zeigende Beschränkung aufzuheben, (vgl.
u.a. Differentialgetriebe)]).
(vgl.
u.a. Differentialgetriebe)]).
 .
.
Von diesen zehn Zahnrädern wählen wir erstmal nur zwei aus:

oder kurz .
.
Dabei sei hier mal angenommen, dass Zahnrad 1 von einem Motor angetrieben wird und dann Zahnrad 2 mitdreht.
 . Dann dreht
sich Zahnrad 2 umgekehrt
gegen den Uhrzeigersinn
. Dann dreht
sich Zahnrad 2 umgekehrt
gegen den Uhrzeigersinn
 :
:

 . Dann dreht sich
Zahnrad 2 umgekehrt
im Uhrzeigersinn
. Dann dreht sich
Zahnrad 2 umgekehrt
im Uhrzeigersinn
 :
:

Aus beiden Fällen zusammen ergibt sich:
| Zwei benachbarte Zahnräder drehen sich in entgegengesetzte Richtungen. |
Wir werden darauf bald zurückkommen, aber vorerst noch etwas Anderes:
die Laufrichtung von Zahnrad 2 folgt (automatisch) aus der von Zahnrad 1. Genau solches "Folge(r)n" macht aber gerade mathematische Beweise aus:
(und evtl. unter Zuhilfenahme bereits anderweitig bewiesener mathematischer Sätze)
(und dann immer so weiter bis zum vollständigen Beweis).
Damit aber schon wieder zurück zu den Drehrichtungen von Zahnrädern:
sehen wir uns als Nächstes in der oben bereits gezeigten Konstellation
eine beliebige Kette vieler nebeneinander liegender Zahnräder an, also z.B.

oder kurz (und schon durchnummeriert):
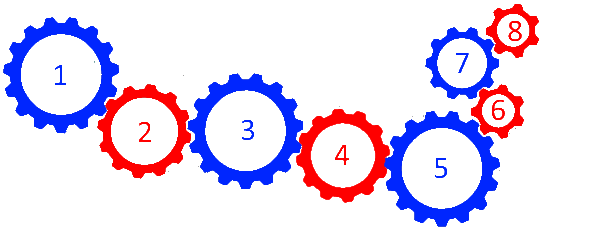
Nun ist es für die Funktionsweise des Zahnrad-Ensembles eigentlich unerheblich, ob die Zahnräder
Hauptsache, sie greifen nacheinander ineinander. Aber für


ordentliche Leute
ordnen wir die Zahnräder trotzdem mal horizontal an
(nebenbei: wenn uns im Folgenden die Drehrichtungen interessieren
[nicht aber die Drehgeschwindigkeiten],
könnten wir sogar alle Zahnräder sogar gleich groß machen - oder genauer: mit derselben Zähnezahl versehen):

Damit haben wir schon eine erste, wenn auch noch ziemlich langweilige Metapher für mathematische Beweise: hier wird in sieben (Zwischen-)Schritten aus der Tatsache 1 die Tatsache 8 hergeleitet, also Tatsache 8 bewiesen:
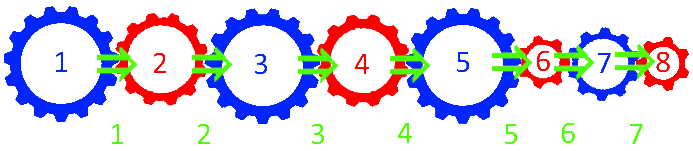
(Dass es egal ist, ob die Zahnräder teils vertikal versetzt oder alle horizontal nebeneinander sind, verweist auf das mathematische Gebiet der "Topologie".)
Allerdings sind Beweise nicht immer so linear (horizontal) hintereinander, sondern in einen Beweis können mehrere vorher bereits bewiesene mathematische Sätze eingehen:
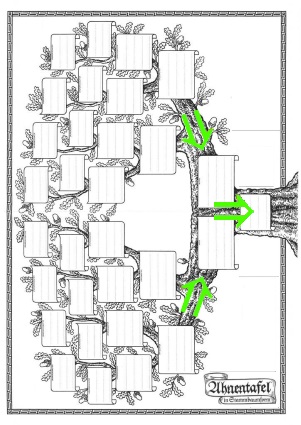
Und so kann sich aus wenigen Anfangsvoraussetzungen (Fundamenten, Axiomen) ein immer komplexeres Geflecht von nacheinander bewiesenen Sätzen ergeben:
Nun gibt es sehr lange mathematische Beweise, die aus mehreren hundert Zwischenschritten bestehen, aber Beweise sind natürlich notgedrungen endlich, denn sonst würde man ja nie mit ihnen fertig (und würde also auch nichts bewiesen).
Das wahrhaft Erstaunliche an der Mathematik ist aber, dass sie
(nochmals: als einzige Wissenschaft)
führen kann.
Beispiel sei da der Beweis des "Satz des Thales", der für
gilt. In der folgenden Version dauert der Beweis aber nur ein bisschen mehr als drei Minuten:
Interessanter wird's, wenn wir nun die Drehrichtungen in

betrachten.
Wieder sei davon ausgegangen, dass Zahnrad 1 angetrieben wird und dann sukzessiv die Zahnräder 2 bis 8 mitdreht.
Gehen wir nun von Folgendem aus:
|
Nun folgt immer mit 2.:
 dreht, dreht
sich Zahnrad 2 gegen den Uhrzeigersinn
dreht, dreht
sich Zahnrad 2 gegen den Uhrzeigersinn
 ,
, dreht, dreht sich
Zahnrad 3 im Uhrzeigersinn
dreht, dreht sich
Zahnrad 3 im Uhrzeigersinn
 ,
, dreht, dreht
sich Zahnrad 4 gegen den Uhrzeigersinn
dreht, dreht
sich Zahnrad 4 gegen den Uhrzeigersinn
 ,
, dreht, dreht sich
Zahnrad 5 im Uhrzeigersinn
dreht, dreht sich
Zahnrad 5 im Uhrzeigersinn  ,
, dreht, dreht sich Zahnrad 6
gegen den Uhrzeigersinn
dreht, dreht sich Zahnrad 6
gegen den Uhrzeigersinn
 ,
, dreht, dreht sich
Zahnrad 7 im Uhrzeigersinn
dreht, dreht sich
Zahnrad 7 im Uhrzeigersinn  ,
, dreht, dreht sich Zahnrad 8
gegen den Uhrzeigersinn
dreht, dreht sich Zahnrad 8
gegen den Uhrzeigersinn
 :
:
Zusammengefasst:
im Uhrzeigersinn
 drehen sich die Zahnräder 1,
3, 5 und
7, also alle Zahnräder mit ungeraden
Nummern,
drehen sich die Zahnräder 1,
3, 5 und
7, also alle Zahnräder mit ungeraden
Nummern,
gegen den Uhrzeigersinn  drehen sich die
Zahnräder 2, 4,
6 und 8, also alle Zahnräder mit
geraden Nummern.
drehen sich die
Zahnräder 2, 4,
6 und 8, also alle Zahnräder mit
geraden Nummern.
Oder anders gesagt:
|
(Diese allgemeinere Formulierung hat den Vorteil, dass sie
auch gilt, wenn das Zahnrad 1
gegen den Uhrzeigersinn
 gedreht wird. Aber
wir bleiben im Folgenden erstmal bei dem Fall, dass das
Zahnrad 1 im
Urzeigersinn
gedreht wird. Aber
wir bleiben im Folgenden erstmal bei dem Fall, dass das
Zahnrad 1 im
Urzeigersinn  gedreht wird.)
gedreht wird.)
Das Spielchen lässt sich natürlich immer weiter, also bis ins Unendliche
(bzw., wie es in dem Buch
 heißt, Aschgraue)
heißt, Aschgraue)
fortsetzen:
im Uhrzeigersinn
 drehen sich alle Zahnräder mit ungeraden Nummern, also z.B.
das
1079. Zahnrad,
drehen sich alle Zahnräder mit ungeraden Nummern, also z.B.
das
1079. Zahnrad,
gegen den Uhrzeigersinn
 drehen sich
alle Zahnräder mit geraden Nummern, also z.B. das
4528969730. Zahnrad,
drehen sich
alle Zahnräder mit geraden Nummern, also z.B. das
4528969730. Zahnrad,
Der Vorteil der gefundenen Regel
|
ist, dass wir wissen, wie sich jedes beliebige Zahnrad dreht, dafür aber nicht mehr herausfinden müssen, wie sich alle vorherigen Zahnräder drehen
(was nicht nur ewig lang dauern könnte, sondern ab einem Fehler bei einem einzigen Zahnrad zu Fehlern bei allen folgenden Zahnrädern führen könnte).
Das Verfahren
|
ist aber nichts Anderes als die sogenannte "vollständige Induktion", die eines der wichtigsten Beweisverfahren der Mathematik ist:
|
Wenn man in

alle Drehpfeile oben zeichnet, werden die entgegengesetzten Drehrichtungen schön deutlich, weil die orangen Pfeile nach rechts, die violetten Pfeile hingegen nach links zeigen.
Nicht so schön deutlich wird das, wenn man die orangen Pfeile oben und die violetten Pfeile unten einzeichnet:
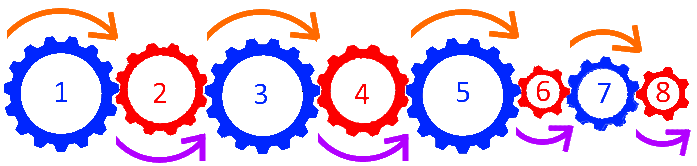
Nun zeigen sowohl die orangen als auch die violetten Pfeile nach rechts, was auf den ersten Blick zu dem Trugschluss führen könnte, alle Zahnräder würden sich in dieselbe Richtung drehen.
Dafür hat diese zweite Darstellungsweise einen anderen Vorteil:
angenommen, wir zeichnen nun die Pfeile näher an die Zahnräder dran

und lassen nun erst die Zahnräder weg

und dann auch noch alle Pfeile bis auf den letzten ganz rechts:

Dann zeigt sich, dass sich die Pfeile wie eine

Schlange
zwischen den Zahnrädern durchwinden, und zwar immer hübsch abwechselnd
 ),
), ):
):Das Sich-Durchwinden erinnert an die berühmte Maschinen-Szene aus Charlie Chaplins Film „Modern Times“:
An diesem Filmausschnitt wird deutlich: damit sich etwas zwischen den Zahnrädern durchwinden kann, dürfen sie sich nicht direkt berühren, d.h. die Zähne benachbarter Zahnräder dürfen nicht ineinander greifen. Dass aber die Kraft dennoch von einem Zahnrad auf das nächste übertragen wird, lässt sich mit einer Kette erreichen:
Mit Lego® ausgedrückt sieht

dann so aus:

Der interessanteste Aspekt von Zahnrad-Anordnungen im Hinblick auf mathematische Beweise ergibt sich aber, wenn man an der ursprünglichen Anordnung

folgenden Ausschnitt betrachtet:

oder kurz .
.
Hier könnte einem auffallen, dass die drei Zahnräder  in
in

eine Schlaufe bilden
(während die Zahnräder in

bzw.

alle hübsch brav hintereinander lagen:
 ).
).
Bevor wir uns nun aber überlegen, wie sich die Zahnräder in  bewegen, bauen wir uns einfach mal solch eine
schlaufenförmige Anordnung dreier Zahnräder mit Lego®, also z.B.
bewegen, bauen wir uns einfach mal solch eine
schlaufenförmige Anordnung dreier Zahnräder mit Lego®, also z.B.  oder
oder  .
.
Beim Versuch, bei diesen Lego®-Modellen eines der drei Zahnräder zu drehen, werden wir (bzw. Schüler) merken:
entweder ist es überhaupt nicht möglich, ein Zahnrad zu drehen,
oder, falls wir deshalb mal fester drehen
("wo rohe Kräfte sinnlos walten"),
die Zähne zweier benachbarter Zahnräder "ratschen" aneinander vorbei,
es brechen sogar Zähne von den Zahnrädern ab,
die Zahnräder springen von ihren Achsen ab,
die Achsen rutschen aus der roten Grundkonstruktion.
Gerade der Umstand, dass es auf praktischem Weg nicht möglich ist, die Zahnräder zu drehen, könnte aber dazu motivieren, sich mal theoretisch zu überlegen, warum das nicht möglich ist.
Nehmen wir bei  wieder an,
Zahnrad 1 werde durch einen Motor in Drehung
versetzt und dann würden nacheinander auch benachbarte Zahnräder angetrieben,
also z.B. so:
wieder an,
Zahnrad 1 werde durch einen Motor in Drehung
versetzt und dann würden nacheinander auch benachbarte Zahnräder angetrieben,
also z.B. so:

(Von wegen "z.B.": genauso gut könnten wir die
umgekehrte
Reihenfolge , betrachten.)
, betrachten.)
In  erfolgt der Antrieb also in der Reihenfolge
erfolgt der Antrieb also in der Reihenfolge
: Zahnrad 1,
: Zahnrad 2,
: Zahnrad 3,
: wieder Zahnrad 1
(Zahnrad 1 treibt sich über Zwischenstufen also selbst an, wobei hier noch unklar ist, was dieser "Selbst-Antrieb" bedeutet).
In diesem Sinne ist Zahnrad 1 also identisch mit Zahnrad 4:
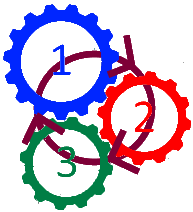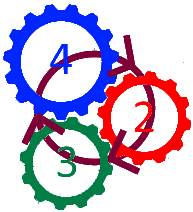
Erinnern wir uns nun an unsere obige Erkenntnis
|
alle Zahnräder mit geraden Nummern drehen sich in die entgegengesetzte Richtung [zur Drehrichtung des Zahnrades 1]. |
Daraus folgt insbesondere:
|
Zahnrad 4 dreht sich in die entgegengesetzte Richtung [zur Drehrichtung des Zahnrades 1]. |
Da nun aber Zahnrad 1 und Zahnrad 4 identisch sind, dreht sich also Zahnrad 1
sowohl in die eine
als auch in die andere Richtung
- und das heißt eben: Zahnrad 1 dreht sich gar nicht
(und in Folge davon drehen sich auch Zahnrad 2 und Zahnrad 3 nicht).
Bislang hatten wir offen gelassen, in welche Richtung das Zahnrad 1 durch den Motor gedreht wird
(es ist auch egal).
Um nun aber besser zu verstehen, was in unserer Argumentation
eben passiert ist, sei hier mal vorausgesetzt, dass das
Zahnrad 1 vom Motor im
Uhrzeigersinn  gedreht wird. Daraus hatten wir gefolgert, dass es (dann als
Zahnrad 4) über die
Zwischenstufen von Zahnrad 2 und
Zahnrad 3 gegen den Uhrzeigersinn
gedreht wird. Daraus hatten wir gefolgert, dass es (dann als
Zahnrad 4) über die
Zwischenstufen von Zahnrad 2 und
Zahnrad 3 gegen den Uhrzeigersinn
 gedreht wird.
gedreht wird.
Unsere Folgerung
 widersprach also
unserer Voraussetzung
widersprach also
unserer Voraussetzung  . Da aber unsere Argumentation durchaus logisch war, muss schon unsere
Voraussetzung
. Da aber unsere Argumentation durchaus logisch war, muss schon unsere
Voraussetzung  falsch gewesen sein.
falsch gewesen sein.
Das aber ist eine schöne Metapher für den mathematischen "Widerspruchsbeweis", bei dem man von einer (vermeintlich richtigen) Voraussetzung ausgeht und sie logisch zu einem Widerspruch zur Voraussetzung oder einer anderen mathematischen Tatsache führt, woraus folgt, dass die (vermeintlich richtige) Voraussetzung in Wirklichkeit falsch war.
Vielleicht der berühmteste Widerspruchsbeweis wird benutzt,
um zu zeigen, dass die ![]() eine irrationale Zahl ist
eine irrationale Zahl ist
In diesem Beweis wird aus Unkenntnis oder einfach mal
probeweise vorausgesetzt, dass
![]() eine rationale Zahl, also
als Bruch zweier ganzer Zahlen darstellbar ist. Außerdem wird als zweite
Tatsache vorausgesetzt, dass dieser Bruch bereits vollständig gekürzt ist.
Daraus wird logisch gefolgert, dass der Bruch nicht vollständig gekürzt war. Da
man aber unzweifelhaft jeden Bruch vollständig kürzen kann, muss schon die
Anfangsvoraussetzung (dass also
eine rationale Zahl, also
als Bruch zweier ganzer Zahlen darstellbar ist. Außerdem wird als zweite
Tatsache vorausgesetzt, dass dieser Bruch bereits vollständig gekürzt ist.
Daraus wird logisch gefolgert, dass der Bruch nicht vollständig gekürzt war. Da
man aber unzweifelhaft jeden Bruch vollständig kürzen kann, muss schon die
Anfangsvoraussetzung (dass also
![]() rational ist) falsch
gewesen sein.
rational ist) falsch
gewesen sein.
(Dass ![]() nicht rational ist, bedeutet aber noch lange nicht, dass
nicht rational ist, bedeutet aber noch lange nicht, dass
![]() eine irrationale Zahl ist.
Es müsste nämlich noch gezeigt werden, dass es die
eine irrationale Zahl ist.
Es müsste nämlich noch gezeigt werden, dass es die
![]() überhaupt gibt
[„Existenzbeweis“].)
überhaupt gibt
[„Existenzbeweis“].)
(Fast) Jedes Modell bzw. jede Metapher
(wenn es bzw. sie denn überhaupt im Hinblick auf das "Original"
[in unserem Fall ein mathematisches Beweisverfahren]
hilfreich ist)
hat im Hinblick auf das gemeinte „Original“ seine bzw. ihre Nachteile:
das Modell bzw. die Metapher kann nur partiell zutreffen;
das Modell bzw. die Metapher kann (deshalb) auch gründlich in die Irre führen.
Ein gutes Beispiel ist da  als Metapher für den mathematischen Widerspruchsbeweis
als Metapher für den mathematischen Widerspruchsbeweis
(hier
am Beispiel des Beweises, dass
![]() irrational ist).
irrational ist).
Halten wir die Parallelen nochmals in einer Tabelle fest:
| Spalte 1 | Spalte 2 | |||
| erste Voraussetzung: | Wenn in  Zahnrad
1 sich in eine Richtung dreht,
Zahnrad
1 sich in eine Richtung dreht, |
Wenn
|
||
| zweite Voraussetzung: | und wenn der Bruch vollständig gekürzt ist, | |||
| erste Folgerung: | dreht sich Zahnrad 4 (das identisch mit Zahnrad 1 ist) in die entgegengesetzte Richtung; | ist der Bruch nicht vollständig gekürzt. | ||
| zweite Folgerung: | Zahnrad 1 dreht sich gar nicht. |
|
Nun gilt Spalte 1
sowohl für den Fall, dass das
Zahnrad 1 im Uhrzeigersinn  gedreht wird (im Folgenden Spalte 1a),
gedreht wird (im Folgenden Spalte 1a),
als auch für den Fall, dass das
Zahnrad 1 gegen den
Uhrzeigersinn
 gedreht wird (im Folgenden
Spalte 1b):
gedreht wird (im Folgenden
Spalte 1b):
| Spalte 1a | Spalte 1b | |||
| erste Voraussetzung: | Wenn in  Zahnrad
1 sich im Uhrzeigersinn
Zahnrad
1 sich im Uhrzeigersinn
 dreht,
dreht, |
Wenn in  Zahnrad
1 sich gegen den Uhrzeigersinn Zahnrad
1 sich gegen den Uhrzeigersinn
 dreht, dreht, |
||
| erste Folgerung: | dreht sich Zahnrad 4 (das identisch mit
Zahnrad
1 ist) gegen den Uhrzeigersinn
 ; ; |
dreht sich Zahnrad 4 (das identisch mit
Zahnrad
1 ist) im Uhrzeigersinn  ; ; |
||
| zweite Folgerung: | Zahnrad 1 dreht sich gar nicht. | Zahnrad 1 dreht sich gar nicht. |
Entsprechend könnte man vermuten, dass oben auch Spalte 2 in beiden "Richtungen" funktioniert, also
sowohl für die Voraussetzung, dass
![]() rational ist (im
Folgenden Spalte 2a)
rational ist (im
Folgenden Spalte 2a)
als auch für die Voraussetzung, dass
![]() irrational ist (im
Folgenden Spalte 2b):
irrational ist (im
Folgenden Spalte 2b):
| Spalte 2a | Spalte 2b | |||
| erste Voraussetzung: | Wenn
|
Wenn
|
||
| zweite Voraussetzung: | und wenn der Bruch vollständig gekürzt ist, | und wenn der Bruch vollständig gekürzt ist, | ||
| erste Folgerung: | ist der Bruch nicht vollständig gekürzt. | ist der Bruch nicht vollständig gekürzt. | ||
| zweite Folgerung: |
|
|
Wir hätten dann zwei Widerspruchsbeweise mit den Ergebnissen
Beides zusammen könnte aber nur bedeuten:
Nun ist in der Argumentation 2b aber ein Fehler:
Obige Gedanken zu
 legen die
Vermutung nahe, dass Zahnrad-Schlaufen immer zu Blockaden führen.
legen die
Vermutung nahe, dass Zahnrad-Schlaufen immer zu Blockaden führen.
Schauen wir uns dazu nochmals die Zahnradkombination

an. Sie enthält noch eine andere Schlaufe, nämlich

oder kurz 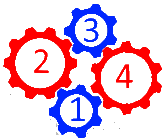 .
.
Angenommen wieder, dass Zahnrad 1 durch einen Motor angetrieben wird. Dann wird die Kraft über Zahnrad 2, Zahnrad 3 und Zahnrad 4 wieder zu Zahnrad 1 weitergegeben, das somit gleichzeitig Zahnrad 5 ist:
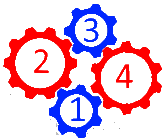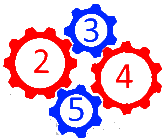
Nach der oben gefundenen Regel
| alle Zahnräder mit ungeraden Nummern drehen sich in dieselbe Richtung wie das Zahnrad 1 |
dreht sich nun aber Zahnrad 5
(das identisch mit Zahnrad 1 ist)
in dieselbe Richtung wie Zahnrad 1, kommt also keine Blockade zustande.
Und in der Tat lässt sich

problemlos drehen.
Die Schlaufe  wäre also nicht als Metapher für mathematische Widerspruchsbeweise geeignet.
wäre also nicht als Metapher für mathematische Widerspruchsbeweise geeignet.
Der Vorteil der Zahnradmetaphern ist, dass Schüler da mathematische Beweisverfahren wortwörtlich sehen und be-greifen können.
Und so können sogar schon Fünftklässler die Gedankengang der "vollständigen Induktion" und des Widerspruchsbeweises verstehen!