
wie die Mathematiker sich die Funktionen zurechtgeschnibbelt haben

Einer der zentralen Begriffe der Mathematik ist die "Funktion", die eine spezielle Art der Zuordnung ist.
Deshalb erstmal eine Erklärung der Zuordnungen:
man kann alles zu allem zuordnen bzw.
(schon mathematisch gesagt)
also z.B.
 (aus der Menge B der Knöpfe).
(aus der Menge B der Knöpfe).(Hier ist ein Einschub zu den
Zuordnungspfeilen
![]() nötig:
nötig:
vielleicht war es mir früher schonmal bewusst, habe ich es inzwischen aber wieder vergessen. Vielleicht fällt es mir aber überhaupt erst jetzt
[nach meiner Lehrertätigkeit und damit zu spät]
auf:
die Schwierigkeiten einiger Schüler mit
Zuordnungen und dann auch
Funktionen liegen vielleicht u.a. darin begründet, dass
Zuordnungspfeile
![]() in der Mathematik genau "andersrum" benutzt werden, als man es im Alltag tut.
in der Mathematik genau "andersrum" benutzt werden, als man es im Alltag tut.
Ein Beispiel:
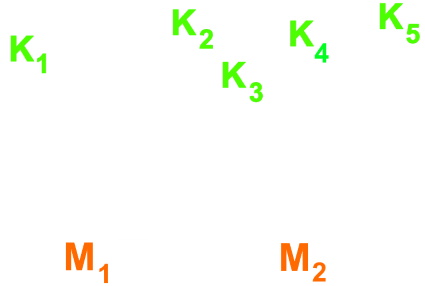
Deshalb hat er die Kinder aufgefordert:
"Liebe Kinder, geht doch bitte mal alle zu eurer Mutter."
Die wohlerzogenen Kinder haben dieser Bitte dann auch umgehend entsprochen, sind also zu ihrer jeweiligen Mutter gegangen
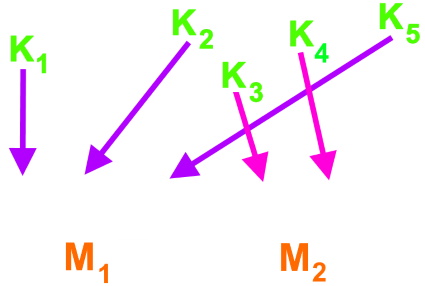 ,
,
so dass sie hinterher so standen:
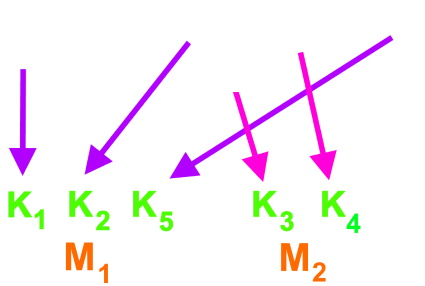
Da sind die Kinder also
auf ihre jeweilige Mutter
zu gegangen, und entsprechend haben die
Pfeile
![]() dann auch
zu den Müttern
hin gezeigt.
dann auch
zu den Müttern
hin gezeigt.
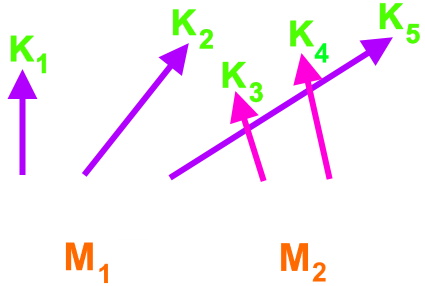
Leider zeichnen die Mathematiker die
Pfeile
![]() aber
genau andersrum, wenn sie den Müttern
ihre Kinder
zuordnen, nämlich nicht auf die Mütter,
sondern auf die Kinder
zu:
aber
genau andersrum, wenn sie den Müttern
ihre Kinder
zuordnen, nämlich nicht auf die Mütter,
sondern auf die Kinder
zu:
Mathematikern ist aber die Möglichkeit, alles zu allem zuzuordnen, aus mehreren Gründen viel zu kompliziert:
Folgerung:
(Schul-)Mathematiker interessieren sich nur für Zuordnungen von Zahlen zu Zahlen:
Zahlen (aus der Zahlenmenge A)Zahlen (aus der Zahlenmenge B)
also z.B. die Zuordnung
- Zahl (aus der Menge der ganzen Zahlen)
ihr Kehrwert (aus der Menge der rationalen Zahlen),
also z.B. 4

= 0,25
- Zahl (aus der Menge der ganzen Zahlen)
ihr Quadrat (aus der Menge der ganzen Zahlen),
also z.B. 3

= 9
Dabei bleibt natürlich alles Individuelle auf der Strecke, denn da wird dann z.B.
- nicht mehr konkret-individuellen Einzelschülern ihre jeweilige (evtl. zumindest in der Klasse ganz eigene und besondere) Schuhgröße zugeordnet (also z.B. Erwin die enorme Schuhgröße 49),
- sondern die SchülerInnen werden gnadenlos durchnummeriert (zu einer Nummer herabgewürdigt), und weil Erwin durch puren Zufall (Sitzreihenfolge) zum Schüler Nr. 17 wird, gilt nur noch
17
49
Wer da die außergewöhnliche Schuhgröße 49 hatte (und weshalb), ist überhaupt nicht mehr erkennbar.
Mehr noch: auch das Zuordnungsergebnis geht unter bzw. wird entwertet (ist nichts besonderes mehr), denn früher oder später ist nicht mal mehr erkennbar, dass es um Schüler und Schuhgrößen ging. Genauso gut könnte Lehrer Nr. 17 einen Intelligenzquotienten von 49 haben oder Atombombe 17 mit 49 Sprengköpfen versehen sein.
So gesehen hat Mathematik was Eiskalt-Abstrakt-Entwürdigendes.
(Oder ist sie doch "wertfrei" wie [angeblich] jede Technik?: z.B. mit einem Hammer kann man Gutes tun [das Foto eines geliebten Menschen befestigen], aber auch Böses [den Menschen erschlagen].)
auszuhalten:
Quadratzahl
ihre Wurzel
gibt es eigentlich zwei zugeordnete Zahlen, nämlich z.B.
9
3 [da 3 2 = 9]
und
9
- 3 [da auch (-3)2 = 9].
Weil Mathematiker solch eine Zweideutigkeit nicht mögen
(und dann die Wurzel-Zuordnung keine Funktion mehr wäre; s.u.),
lassen sie einfach die zweite Lösung - 3 unter den Tisch fallen und für Wurzeln nur noch positive Zahlen (3 bzw. +3) zu, also z.B.
ist eindeutig gleich +3 (und nicht auch -3)
Immerhin holen die Mathematiker die -3 mit einem hübschen Trick dann doch wieder "um die Ecke" rein:
- 3 = - (+3) = - (
) = -
(Man beachte, dass dabei
= + 3 positiv ist und bleibt und erst das Minus in -
daraus die negative Zahl - 3 macht.)
|
|
Erst wenn eine Zuordnung eindeutig ist, ist sie eine Funktion. |
Die Eindeutigkeit kann man sich besonders gut anhand des folgenden Beispiels merken:
(nebenbei:
"Eindeutige Zuordnung" bedeutet bei Funktionsgraphen,
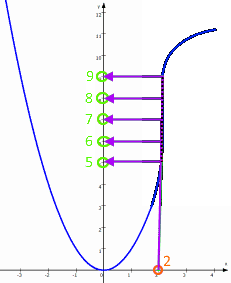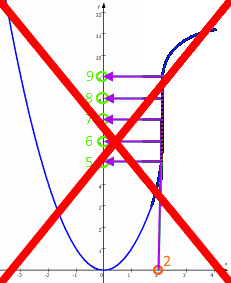 werden dann
x =
2 massenhaft y-Werte
zugeordnet, nämlich z.B.
y
= 5,
y =
6,
y =
7,
y =
8 und
y =
9
(und alle Zwischenwerte);
werden dann
x =
2 massenhaft y-Werte
zugeordnet, nämlich z.B.
y
= 5,
y =
6,
y =
7,
y =
8 und
y =
9
(und alle Zwischenwerte); werden
dann z.B. x = 1
zwei y-Werte
zugeordnet, nämlich
y = 1 und
y
= 10,5.
werden
dann z.B. x = 1
zwei y-Werte
zugeordnet, nämlich
y = 1 und
y
= 10,5.| 3. | Funktionen laufen nach einer einzigen Regel ab. |

"Vor dem
Gesetz sind alle gleich."
(oder sollten es sein)
(Allerdings kann man auch zwei verschiedene Funktionen wählen, von denen z.B. die eine nur die Wurzel zieht und die andere nur quadriert
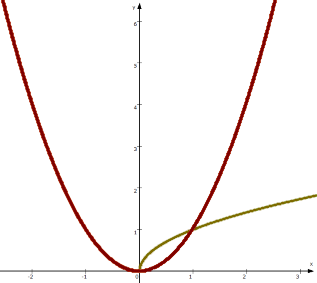 ,
,
und diese dann zu einer Gesamtfunktion zusammensetzen, indem man z.B. sagt, für negative Zahlen solle immer quadriert und für positive Zahlen immer die Wurzel gezogen werden:
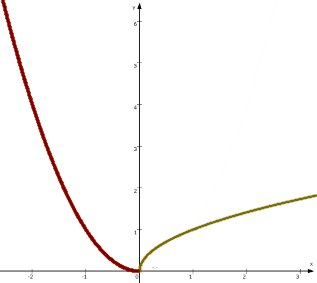
Man sagt dann auch, die Gesamtfunktion sei "stückweise" durch unterschiedliche Funktionen definiert
[was allerdings im Schulunterricht kaum jemals vorkommt].)
| 4.: | Funktionen sind nur von einer einzigen Variablen (meistens x) abhängig. |
Z.B. wird die Fläche F eines Rechtecks berechnet als F ( Länge , Breite ) = Länge • Breite.
Oder kurz: F ( l , b ) = l • b .
Dabei bedeutet F ( l , b ), dass die Fläche des Rechtecks
sowohl von der Variablen l
als auch von der Variablen b abhängig ist.
Wir können also



In allen drei Fällen wurde eine Verdopplung der Fläche von 20 cm2 auf 40 cm2 erreicht.
Wenn wir aber nur wissen, dass solch eine Verdopplung der Fläche erreicht wurde, wissen wir nicht, wie diese Verdopplung zustande gekommen ist:
Eine Analogie macht klar, warum solche Unklarheit ungünstig ist:
angenommen mal, die Schaltung eines Fahrrads funktioniert (!) nicht mehr richtig. Dann können wir an zwei Schrauben drehen:


 und
und
 gleichzeitig.
gleichzeitig.
Angenommen nun mal, wir haben an
 und
und
 gleichzeitig
gedreht (Fall c.).
gleichzeitig
gedreht (Fall c.).
(Oder genauer: erst an der vorderen Schraube und dann
[ohne zu überprüfen, ob das das Drehen vorne eine Verbesserung gebracht hat]
an der hinteren.)
Wenn das Drehen an beiden Schrauben zu keiner Beseitigung der Schaltprobleme geführt hat, bestünde die Möglichkeit, dass
das Drehen an
 (Fall a.) sehr
wohl zu einer Beseitigung der Probleme geführt hat,
(Fall a.) sehr
wohl zu einer Beseitigung der Probleme geführt hat,
diese Verbesserung aber
durch das Drehen an  (Fall b.) rückgängig gemacht wurde.
(Fall b.) rückgängig gemacht wurde.
Dann bemerken wir gar nicht die Verbesserung
durch das Drehen an  (Fall a.) - und suchen vielleicht nach einer anderen, evtl. gar nicht vorhandenen Fehlerursache.
(Fall a.) - und suchen vielleicht nach einer anderen, evtl. gar nicht vorhandenen Fehlerursache.
Daraus folgt die alte Handwerkerregel:
| Drehe nie an mehreren Schrauben gleichzeitig! | |
|
Bei Funktionen kommt hinzu, dass sämtliche Gesetze, die man im Unterricht kennengelernt hat (also z.B. die pq-Formel
nur für Gleichungen funktionieren (!), in denen nur noch eine einzige Variable (meistens x) vorkommt! |
Fassen wir also zusammen, wie die Mathematiker ihr Blickfeld immer
weiter eingeengt haben
 :
:
| 0. | Man kann
|
 |
| 1. | Mathematiker interessieren sich nur für
Zuordnungen
|
|
| 2. | Erst wenn eine Zuordnung eindeutig ist, ist sie eine Funktion. | |
| 3. | Funktionen laufen nach einer einzigen Regel ab. | |
| 4. | Funktionen sind nur von einer einzigen Variablen (meistens x) abhängig. |