Heiner Stauff - anschauliche Mathematik

... was natürlich nur die drittbeste Lösung ist:

die (erst-)beste Lösung wäre, dass der Leser ein echtes, be-greifbares Daumenkino mit Funktionsgraphen durchblättern würde, was virtuell-online allerdings nicht möglich ist;
die zweitbeste Lösung wäre, dass ich ein echtes Funktionen-Daumenkino bastle und hier immerhin einen Film davon einstelle ... was mir allerdings zu aufwendig ist;
die drittbeste Lösung ist eben, (wie oben unschön geschehen) mittels Bildbearbeitung in einen fertigen Daumenkino-Film Funktionsgraphen einzumontieren;
die viertbeste und damit schlechteste, weil völlig unanschauliche Lösung wäre aber, das Daumenkino gar nicht zu zeigen, sondern nur "drüber" zu reden.

Schauen wir uns zuerst eine einzelne Funktion, nämlich z.B. f: y = , an: sie ist eine Maschine

x rein →

Bild

→ y =

raus

(vgl. )

mit zwei widersprüchlichen Eigenschaften:

einerseits ist sie strubbeldumm, kann nämlich nichts Anderes als ewig nur quadrieren,
andererseits ist sie geradezu übermenschlich allmächtig, kann nämlich alle reellen, also unendlich viele Zahlen quadrieren

(solch eine Funktion erinnert an Computer, die

gleichfalls dumm sind, aber immerhin
extrem schnell rechnen können;

und dennoch hinkt [wie wir noch sehen werden] der Vergleich mit Computern, da diese zwar rasend schnell, aber - im Gegensatz zu Funktionen - nicht mit unendlich vielen Zahlen rechnen können).

Bleiben wir kurz bei

"kann [...] ewig nur quadrieren" und
"kann [...] unendlich viele Zahlen quadrieren".

Hier stellt sich die uralte Frage nach dem - anspruchsvoll gesagt - "aktual" oder "potentiell" Unendlichen:

kann (könnte = Irrealis) die Funktion

(wie ein Mensch oder auch ein Computer)

nur vom Prinzip her alle (= unendlich viele) reellen Zahlen quadrieren, würde dafür aber doch ewig brauchen (= potentiell unendlich),

oder tut sie es tatsächlich in endlicher Zeit, nämlich sogar in einem einzigen Augenblick, also im selben Moment, in dem sie "geboren" wird (= aktual unendlich)?

(Dabei wäre das "aktual Unendliche" doch geradezu skandalös paradox: wie soll es denn möglich sein, in endlicher Zeit

[oder noch unglaublicher: in einem Augenblick, also einer Zeitspanne der Länge Null]

unendlich viele Fälle

[beim Augenblick sogar gleichzeitig]

"abzuhaken"???

Und doch ist genau das der Kern der Mathematik, der sie von allen anderen Wissenschaften unterscheidet: dass sie z.B. in endlicher Zeit [ca. 30 Sekunden] beweisen kann, dass in allen (= unendlich vielen) ebenen Dreiecken die Winkelsumme 180⁰ ist!!!)

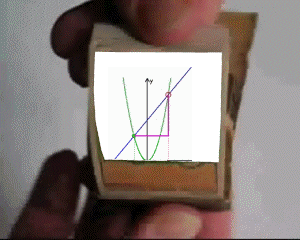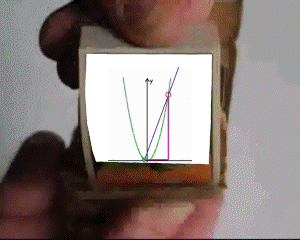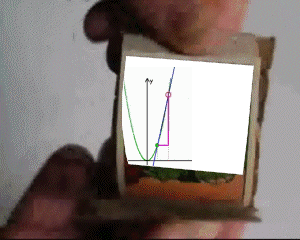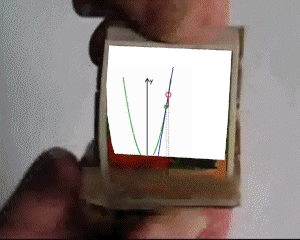
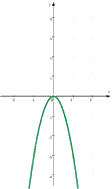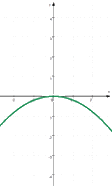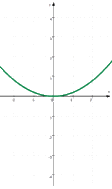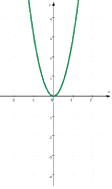
Ich meine in der Tat, dass die Quadriermaschine f aktual unendlich ist, und zwar sogar in einem einzigen Augenblick: die Funktion f mit der Funktionsgleichung y = "ist" nämlich gleichzeitig ihr Funktionsgraph

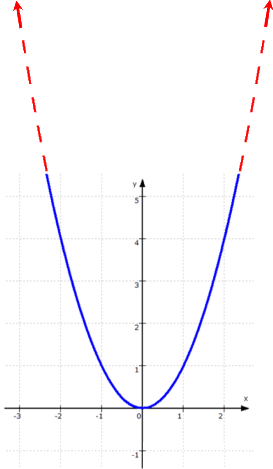
Und selbst wenn die beiden "Arme" nicht unendlich hoch steigen, wenn also nicht sehr große negative oder positive x berücksichtigt wurden, können wir uns diese "Arme" eben doch dazu denken.

Vor allem aber ist der gezeichnete Graph "stetig", d.h. mit einem durchgehenden Strich gezeichnet, und das heißt, dass bereits in diesem kleinen Intervall unendlich viele reelle Zahlen berücksichtigt wurden.

(Unsere Phantasie reicht da weiter als unsere Rechenfertigkeiten oder die eines Computers: wir selbst wie auch ein Computer berechnen natürlich immer nur einige wenige [endlich viele] Punkte des Graphen - und verbinden/t sie dann mit einem durchgehenden Strich

[der Computer berechnet viel mehr Punkte als wir und verbindet sie dann mit sehr kurzen [geraden!] Strecken, die aber so klein sind, dass wir alle zusammen für eine gebogene Kurve halten]).

Und selbst wenn die Punkte des Graphen nacheinander eingezeichnet werden

(also nacheinander die y- zu den wachsenden x-Werten berechnet werden),

entsteht eine stetige Linie mit unendlich vielen dichtgepackten Punkten

(auch das ist wieder "nur" theoretisch möglich).

Bereits dadurch wäre für jede Einzel-Funktion

(hier f: y = )

ein Daumenkino möglich:

(Hier ist Zeit, sich statt des Daumenkinos einen Film[-ausschnitt] vorzustellen:

Der nötige Film-Transportmechanismus müsste dabei

[wie bei echten Filmprojektoren]

einerseits bei jedem Einzelbild kurz anhalten,
andererseits danach den Film bis zum nächsten Bild weiterziehen,
und beides rasend schnell abwechselnd:

Das aber wäre

- wenn überhaupt - nur mit größtem mechanischem Aufwand machbar
und auch kaum ein geeignetes geistiges Veranschaulichungsbild.)

Aus zwei Gründen halte ich wenig davon, wenn SchülerInnen sich fertige

Parabelschablone(n)

kaufen:

sind diese Parabelschablonen eben fertig, d.h. die SchülerInnen lernen nicht, wie der Funktionsgraph im Koordinatensystem entsteht und wie man ihn sehr einfach konstruieren kann:

zeigt die Parabelschablone nur den Graphen der "Normal"-Parabel, also der Funktion f: y = , und somit

nur einen einzigen Funktionsgraphen, obwohl es doch
unendlich viele quadratische Funktionen gibt.

Nun sind aber MathematikerInnen, wenn irgend möglich, nie an Einzelfällen, sondern an weitest möglichen Verallgemeinerungen interessiert, also z.B. an

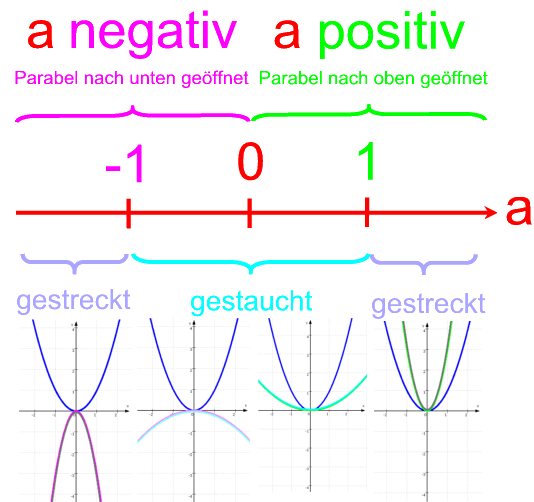
allen (also unendlich vielen) quadratischen Funktionen

(wie sich zeigen lässt, sind sie alle ebenfalls "parabelförmig", wenn auch evtl. gestreckt oder gestaucht [siehe B.], und ihre Funktionsgleichungen haben die Form f: y = ax² +bx + c)

oder zumindest an allen (auch schon unendlich vielen) quadratischen Funktionen, die ihren Scheitelpunkt im Ursprung des Koordinatensystems haben.

Zu A.: hier tauchen in f: y = ax² +bx + c drei sogenannte "Formvariable" auf

(was genau darunter zu verstehen ist, wird weiter unten gezeigt),

nämlich a, b und c, und da es nicht möglich ist,

an allen dreien gleichzeitig und dennoch systematisch zu "drehen",
ein (!) Daumenkino dafür zu bauen,

sei diesem Fall A. hier nicht weiter nachgegangen.

Zu B.:, also allen (unendlich vielen!) quadratischen Funktionen,
die ihren Scheitelpunkt im Ursprung des Koordinatensystems haben:

Wir schauen uns hier im Ball B. nur die quadratischen Funktionen mit den Funktionsgleichungen f: y = an, also ohne die Folgeterme bx + c aus A.

(... was nebenbei auch deshalb "sinnig" ist, weil

[wie sich zeigen ließe]

die Folgeterme bx + c

nichts mehr an der Form des Graphen von f: y = ,
sondern nur noch dessen Lage verändern

[vertikale und/oder horizontale Verschiebung]).

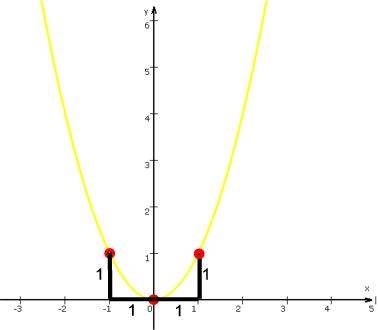
Schauen wir uns nun f: y = genauer an, und zwar erstmal nur für den Spezialfall a = 3, also f: y = . Dabei

gibt der Bestandteil die grunsätzliche Form einer quadratischen (Normal-)Parabel vor:

sorgt der Bestnadteil 3 "nur" dafür, dass jeder Wert der (Normal-)Parabel verdreifacht wird, die Ergebnisparabel also drei Mal so hoch liegt:

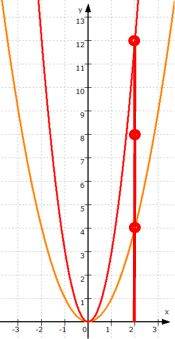
(Vorsicht: "drei Mal so hoch" heißt

nicht "um 3 höher"

[was insbesondere bedeuten würde, dass auch der Scheitelpunkt um 3 nach oben wandern würde; vielmehr gilt ... ],

, ... dass der Scheitelpunkt der neuen Parabel im Ursprung bleibt;

vgl. )

In

ist also die Normalparabel zur Ergebnisparabel gestreckt worden.

Im Schnelldurchgang:

jede Parabel mit der Funktionsgleichung f: y = ist

(im Vergleich mit der Normalparabel)

gestreckt für |a| > 1 :

Bild

gestaucht für |a| < 1 :

Bild

nach oben geöffnet für positive a, also für a > 0 ,
nach unten geöffnet für negative a, also für a < 0 ,

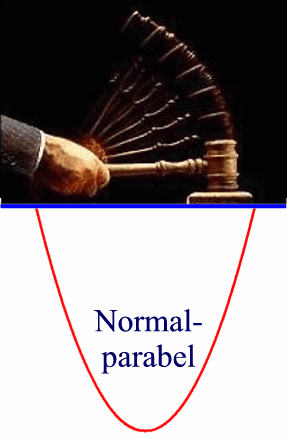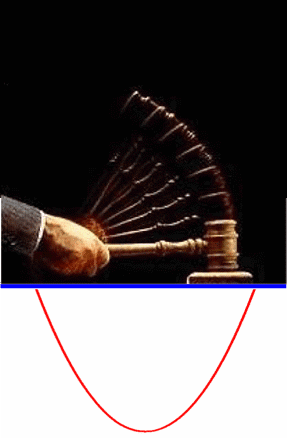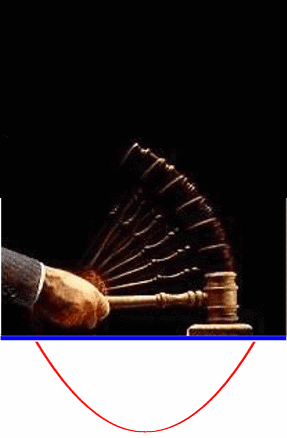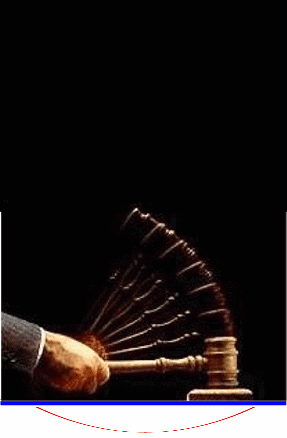
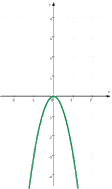
so dass sich insgesamt ergibt:

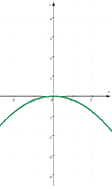
(jeweils im Vergleich mit der Normalparabel)

Wenn wir nun jeweils die Normalparabel weglassen, so ergibt sich von links nach rechts, also für wachsendes a

,

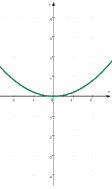
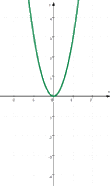Diese vier Parabeln kann man nun auch in ein einziges Koordinatensystem zeichnen:

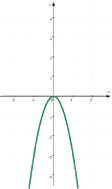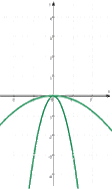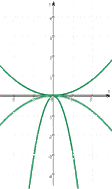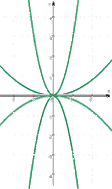
Möglichkeit: man läst die vorherigen Graphen stehen:

Möglichkeit: man zeichnet jeweils nur einen Graphen, löscht also die vorherigen:

Auch wenn hier bislang nur vier Zustände eingezeichnet sind, sieht es doch schon so aus, als wenn

sich da eine einzige Parabel (allerdings noch sehr "ruckelig") immer mehr nach oben öffnet und "der Sonnen engegenstreckt"

,

die einzelne Parabel sich also bewegt (vgl. ).

In den beiden Fällen 1. und 2. stellt sich gleichermaßen die Frage, was passieren würde, wenn man alle (= unendlich viele!) Parabeln einzeichnen würde, die ihren Scheitelpunkt im Ursprung des Koordinatensystems haben. Wir werden unten darauf zurückkommen, stellen aber vorerst mal klar:

für jedes einzelne a entsteht mittels f: y =

eine eigene Parabel, also z.B.

für a = 1 die Normalparabel,
für a = 3 eine gestreckte , nach oben geöffnete Parabel,
für a = - 0,2 eine gestauchte, nach unten geöffnete Parabel.

Insgesamt entstehen also

für die unendlich vielen möglichen a
auch unendlich viele Parabeln.

In all diesen unendlich vielen Fällen liegen quadratische Parabeln vor. Ansonsten entscheidet sich die Form

(gestreckt/gestaucht, nach oben/unten geöffnet)

der jeweiligen Parabel aber an dem a, weshalb man es auch "Formvariable" nennt.

Wenn also die Funktionsgleichung f: y =

auftaucht,

wählt man zuerst für die Formvariable a einen beliebigen konkreten Wert, also z.B. a = - 7,
und erhält dann die zugehörige konkrete Funktionsgleichung, also z.B. f: y =

(immer in dieser Reihenfolge!).

Durch die allgemeine Gleichung f: y =

entstehen also unendlich viele Parabeln, und man spricht dann auch von einer Funktionen- bzw. Parabelschar.

Wir können also festhalten:

durch f: y = entstehen unendlich viele Parabeln , und
in jede einzelne Parabelgleichung (z.B. für a = -7) kann man wiederum unendlich viele x einsetzen und somit die zugehörigen y erhalten:

Funktionenscharen handeln also von unendlich mal unendlich vielen bzw. unendlich² Fällen!

(... womit sich ein hochinteressantes mathematisches Thema andeutet, nämlich eine

[für den "gesunden Menschenverstand" doch allemal unvorstellbare bzw. blödsinnige]

Steigerung von "unendlich": "unendlich, unendlicher, am unendlichsten"??? Vgl. )

Unsere gesamte Überlegungen würde also bedeuten, dass wir zur Darstellung von "unendlich mal unendlich"

zu jeder möglichen Einzelfunktion ein Daumenkino der Art , also schon allein hierfür unendlich viele Daumenkinos und
nochmal ein (einziges) Daumenkino der Art brauchen würden.

Schon allein der Fall a. ist unmöglich: wir können nicht

(wenn wir es überhaupt wollten)

unendlich viele Daumenkinos herstellen, ja, selbst die Herstellung von - sagen wir mal - "nur" 100 Daumenkinos wäre allzu umständlich.

(Genau genommen können wir ja nicht mal

[und zwar aus mehreren, unten noch genauer zu betrachtenden Gründen]

das eine Daumenkino aus b. mit allen, also unendlich vielen Einzelparabeln herstellen.)

Aber die Grenzen des Modells liegen auch noch woanders: es wäre ja nicht so, dass wir

erst à la das Entstehen aller Einzelparabeln und
danach mittels deren Bewegung nach oben zeigen müssten,

sondern der korrekte Verlauf wäre ja wohl:

Entstehen der ersten Parabel,
Entstehen der zweiten Parabel,
Entstehen der dritten Parabel
...

Wegen der zwischenzeitlichen langwierigen Entstehung jeder Einzelparabel würde dadurch aber der Effekt der sukzessiven Bewegung der aufeinander folgenden Einzelparabeln zu lange unterbrochen und somit "unsichtbar".

Damit aber zurück zu Fall 1., also :

Hier sieht es (anders als in Fall 2.) eher so aus, wie es tatsächlich ist:

da bewegt sich nicht eine einzige Parabel,
sondern es werden nacheinander weitere Parabeln dazu gezeichnet.

(... weshalb der Plural "Funktionenschar" angebracht ist).

Obwohl es technisch nicht möglich ist, wäre dennoch die Frage interessant, was passieren würde, wenn wir alle, also unendlich viele Parabeln einzeichnen würden:

würde, da ja Funktionen vorliegen, keine der möglichen Parabeln senkrecht, d.h. es liegen (außer dem Ursprung) keine Punkte auf der y-Achse;
kann man sich streiten, ob man im Fall a = 0, also für f: y = = 0 , überhaupt noch von einer "Parabel" sprechen möchte, da der Funktionsgraph von f: y = = 0 eine Gerade auf der x-Achse ist, also nichts Parabelförmiges mehr an sich hat; wir entscheiden uns hier mal dafür, in diesem Fall nicht von einer Parabel zu sprechen, die Gerade (x-Achse außer Ursprung) also nicht einzuzeichnen;
werden ansonsten aber alle Punkte des Koordinatensystems durch irgendeine Parabel durchlaufen.

Aus A. bis C. würde folgen, dass alle Parabeln zusammen so aussehen:

:

das Koordinatensystem wäre komplett ausgefüllt - mit zwei Ausnahmen:
nur die x- und die y-Achse blieben leer,
dennoch wäre aber auch der Ursprung (= einzelner Punkt!) des Koordinatensystems "ausgefüllt".

Besser verdeutichen lässt sich das mit einem Negativ, auf dem nur die Punkte weiß bleiben, durch die keine einzige der vielen Parabeln geht:

Wenn man aber die Gerade als vollends plattgestauchten Spezialfall der Parabeln akzeptiert, sieht das Gesamtergebnis so aus:

Und nun (nochmal) zum 2. Fall, also :

Hier sieht es - wie schon oben erwähnt - so aus, als wenn

nicht mehrere (vier) Parabeln nacheinander erscheinen,
sondern eine einzige Parabel sich (wenn auch noch sehr abgehackt) immer mehr nach oben öffnet

(weshalb man auch im Singular von einer "Funktionsschar" sprechen könnte).

Und schon sind wir bei den typischen Grenzen bzw. gefährlich suggestiven Irrwegen von Modellen: natürlich ist der Eindruck, dass sich da eine einzige Parabel bewegt, schlichtweg falsch.

Und doch hat die Darstellung auch ihre Vorteile:

wir haben mit ihr zum ersten Mal in der "Funktionenlehre" , d.h.
die Graphen stehen nicht mehr so apathisch in der Landschaft rum

(wenn sie auch noch immer abgenagt-magersüchtig sind, nämlich theoretisch die Breite Null haben; das ändert sich erst bei Fraktalen: );

ist schlichtweg ästhetischer und vermutlich deshalb auch besser merkbar.

Wirklich interessant wird ein Veranschaulichungsmittel wie eben hier

das Daumenkino

aber erst, wenn es nicht in einem Einzelfall wie z.B. Funktionenscharen hilfreich ist, sondern ein mehrfach anwendbares Prinzip bzw. eine grundlegende mathematische Denkweise verdeutlicht:

"The branch of mathematics called calculus was introduced by Newton and Leibniz precisely to permit a rigorous analysis and an accurate modeling of both motion and change. By now, this incredible tool has become so potent and all encompassing that it can be used to examine problems as diverse as the motion of the space shuttle or the spreading of an infectious disease. Just as a movie can capture motion by breaking it up into a frame-by-frame-sequence, calculus can measure change on such a fine grid that it allows for the determination of quantities that have only a fleeting existence, such as instantaneous speed, acceleration, or rate of change."
(zitiert nach , wobei mir an diesem Zitat zweierlei bemerkenswert erscheint:

, dass da - wie so oft - ein Autor vorher etwas Ähnliches wie ich geschrieben hat, ich es aber erst nachher erfahre;
, dass das Zitat für mich fast Anlass wäre, einen eigenen Essay mit dem Titel "die Pracht der Mathematik" zu schreiben: ist es nicht schier unfassbar, was der "calculus" alles leisten kann?! [Und nebenbei: mir gefällt natürlich ungemein das leider veraltete Wort "Pracht.)

Livio macht also darauf aufmerksam, dass eine der Großtaten der Mathematik, nämlich das Differenzieren, auch mit einem Film bzw. Daumenkino veranschaulicht werden kann: