Origami und 
Pop-up'sin den Matheunterricht!
Origami und Pop-up's
in den Matheunterricht!
(... wobei ich hier in der Überschrift bewusst keine
mathematischen Gegenstände,
sondern Dinosaurier gewählt habe.)
Zwei Wege haben mich zu diesem Aufsatz geführt:
ist mein Sohn derzeit auf dem Astronautentripp und wollte daher, seitdem er es einmal in einer Buchhandlung gesehen hatte, ein Buch haben, das er nach langem Quengeln dann auch tatsächlich bekommen hat - und zwar letztlich wohl, weil es auch dem "Kind im Manne" des Vaters so gut gefiel:
"Pop up" bedeutet dabei, dass in den Büchern "Gegenstände" zusammengefaltet sind, die sich beim Öffnen der Buchseiten automatisch entfalten.
Faszinierende Beispiele aus dem "Mondlandung"-Buch sind
zusammengefaltet:
auseinandergefaltet:
.
Aber wieso sind solche Pop-up-Büchern eigentlich so faszinierend?: weil
(also sozusagen aus dem zwischen zwei Seiten verborgenen Nichts)
Dreidimensionales entstehen kann und
(man beachte den Gegensatz "mühelos ↔ komplizierteste"!).
Vgl. auch
Paul Jackson: The Pop-Up Book;
Step-By-Step Instructions for Creating Over 100 Original Paper Projects; Henry Holt
The POP-UP World of Ann Montanaro
die (nicht meine) Entdeckung, dass die klassischen (und klassisch angeblich unlösbaren) Probleme "Winkeldreiteilung" und "Würfelverdopplung" sehr wohl, wenn auch auf "unklassische" Art lösbar sind, und zwar mittels Origami
(vgl. 
),
womit Origami für mich erstmals nicht mehr
(wie ich bis dahin gedacht hatte)
nur das neckische Basteln hübscher Blüten 
war.
Das in westlichen oder zumindest deutschen Ohren Abstoßendste
(und das hat vermutlich sogar pädagogische Konsequenzen; s.u.)
oder zumindest Irreführendste ist der niedlich vokalschwangere Name "Origami".
"Origami (jap. 折り紙, von oru = falten + kami = Papier) ist die Kunst des Papierfaltens.
Ausgehend von einem zumeist quadratischen Blatt Papier entstehen allein durch Falten 2- oder 3-dimensionale Objekte wie z. B. Tiere, Vögel, Oriplane [= Papierflieger], Gegenstände und geometrische Körper. Dabei sind speziell im westlichen Kulturkreis Schere und Klebstoff zum Teil absolut verpönt."
(Quelle: ; beachte dort auch erste weiterführende Hyperlinks)
"Niedlich" ist es nämlich keineswegs immer, was da zustande kommt, sondern teilweise
(allerdings dann oftmals doch mit Schneiden und Kleben)
überaus erstaunlich:
Wenn ich Origami und Pop-up-Bücher in den Mathematikunterricht bringen will, so vor allem aus nur indirekt mathematischen Gründen: weil ich mir dadurch bei den SchülerInneN
größere Sorgfalt und
ein besseres räumliches Vorstellungsvermögen,
aber auch Spaß am und Stolz auf das Selbstgemachte
erwarte.
Und ich wette, dass solch ein "indirekter" Matheunterricht um die Ecke dann eben doch sehr viel mehr für
brächte als monatelanger Standardunterricht!
Für solch ein Projekt sollte viel Zeit zur Verfügung stehen, und dafür kann meinetwegen massenhaft stumpf durchgepaukter Standardstoff inkl. der Klassenarbeiten ausfallen.
Wie oben schon angedeutet, glaube ich aber nicht, dass die SchülerInnen bei solch einem Unterrichtsprojekt unisono "Hurra!" schreien würden:
: "das ist gar keine Mathematik, und wenn ich Mathematik bezahlt habe, kann ich auch verlangen, dass Mathematik drin ist";
, weil so ein Projekt allzu sehr von dem gewohnten Standard-Stumpf-Mathematik-Unterricht absticht,
weil die SchülerInnen nicht weniger, sondern mehr tun müssten
(Schulstunden nicht abhängen, sondern in ihnen basteln, ja sogar zu Hause weiterbasteln),
ungeliebte und nicht als sinnvoll erkannte handwerkliche Qualitätsansprüche,
: "schon meine Großmutter war handwerklich vollständig unbegabt",
: "pisseliges Basteln [z.B. mit Peddingrohr] ist mir zu unmännlich bzw. Konstruktives zu unweiblich".
Einen Vorteil haben Origami und Pop-up's aber allemal: im Gegensatz zu sonstigem, allemal in Schulen wünschenswertem Modellbau-Basteln
ist das Material
(Papier, Pappe)
spottbillig
und braucht man auch kein großartiges Werkzeug
(fürs hardcore-Origami höchstens ein Lineal, ansonsten nur Schere und Kleber),
das nunmal in vielen Schulen nicht vorhanden ist.
Mit "Winkeldreiteilung" und "Würfelverdopplung" war allerdings auch schon angedeutet worden, dass zumindest Origami auch direkt mathematisch ist. Ein Beispiel ist das oben bereits gezeigte
,
also schlichtweg ein "Buckyball", der nicht nur ästhetisch, sondern auch mathematisch und physikalisch-nanotechnisch hochinteressant ist:
Wir bauen einen Buckyball!
Fullerene
Richard Buckminster Fuller
Zum Origami und seinen mathematischen Aspekten vergleiche auch:
Origami & Math
Math and Origami
Mathematics of paper folding
Origami Deutschland e.V.
Geomancy
Der Pool von Origami Around the World
Eigentlich müßig, es überhaupt zu erwähnen: natürlich sollen die SchülerInnen in der hier angedachten Unterrichtseinheit nicht nur fertige Origami-Figuren und Pop-up-Bücher konsumieren, sondern diese sind überhaupt nur als Appetizer sowie dazu gedacht, von ihnen Tricks (Falttechniken ...) abzukupfern.
Danach werden zuerst nach fertigen Bauplänen, später aber vielleicht auch frei geplant erst einfache, dann zunehmend komplexe Figuren selbst gebastelt.
(Und die Ergebnisse werden später - solange sowas sein muss - im Range von Klassenarbeiten benotet!)
PS:
meine Faszination für Papierfalttechniken stammt schon aus meiner Kindheit, wenn ich da auch noch gar nicht das "richtige" Origami kannte: ich habe damals sehr gern aus Papier und Pappe Gegenstände (Kästchen, Gebäude) gebaut und mir dabei selbst eine geradezu
(den Begriff kannte ich natürlich auch noch nicht:)
topologische Beschränkung auferlegt: dass zwar
(im Gegensatz zum hardcore-Origami)
geschnitten und geklebt werden durfte, aber alles aus einem einzigen, zusammenhängenden Stück Papier bzw. Pappe sein musste, und ich empfand es damals als regelrechte Herausforderung, was sich so alles unter dieser rigiden Voraussetzung (nicht) herstellen ließ.
Ein schönes Problem in genau diesem Sinne wäre gewesen: ist es möglich, einen
Würfel mit "Tunnel" mittendurch,
und zwar mit ausgekleideten Seitenwänden
aus einem einzigen, zusammenhängenden Stück Pappe zu bauen?
Ich sowie andere Mathematiklehrer hielten das auf Anhieb für aus topologischen Gründen unmöglich, wurden dann aber von der Schülerin Viola Ackfeld eines Besseren belehrt:
Der "Trick" besteht dabei darin, dass man die Tunnelwände nicht aus den Seitenwänden des Würfels herausarbeitet
(was natürlich nicht funktioniert),
sondern ihn "umwickelt":
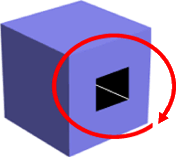
Eine von Niklas Muckermann gefundene weitere Lösung:
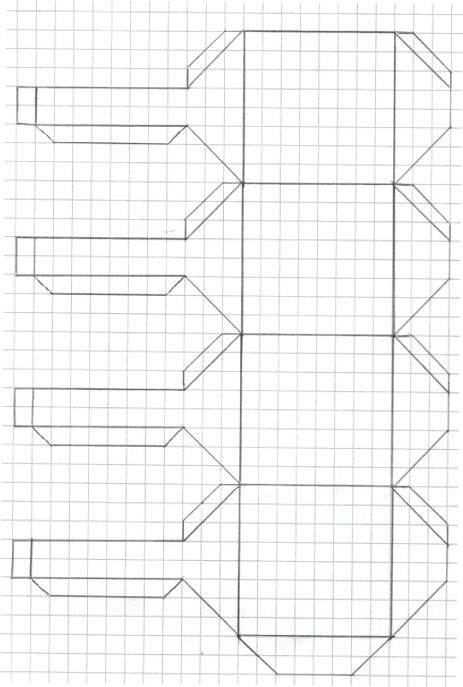
Bei solch frühkindlichen Faszinationen wie eben meiner für Origami ist allerdings pädagogische Vorsicht geboten: SchülerInnen sind nicht dazu da, die persönliche Nostalgie des Lehrers auszuleben. Man kann von ihnen keine spezielle Begeisterung verlangen, nur weil man selbst sie mal gehabt hat.
Vgl. auch
("Kunst im öffentlichen Raum" in New York)