die vielfältige mathematische Nützlichkeit der

	"Die Schlangen-Linie halte ich für ein Buch für die dienlichste, und ich hatte schon in dieser Linie geschrieben, [...] ehe Tristram Shandy seine Manier en Ziczac oder Ziczac à double Ziczac bekannt machte, so ohngefähr: ." (Georg Christoph Lichtenberg)
(Michelangelo: Sixtinische Kapelle)	"Und Gott der HERR pflanzte einen Garten in Eden gegen Osten hin und setzte den Menschen hinein, den er gemacht hatte. Und Gott der HERR ließ aufwachsen aus der Erde allerlei Bäume, verlockend anzusehen und gut zu essen, und den Baum des Lebens mitten im Garten und den Baum der Erkenntnis [...] Aber die Schlange war listiger als alle Tiere auf dem Felde, die Gott der HERR gemacht hatte, und sprach zu dem Weibe: Ja, sollte Gott gesagt haben: ihr sollt nicht essen von allen Bäumen im Garten? Da sprach das Weib zu der Schlange: Wir essen von den Früchten der Bäume im Garten; aber von den Früchten des Baumes mitten im Garten hat Gott gesagt: Esset nicht davon, rühret sie auch nicht an, daß ihr nicht sterbet! Da sprach die Schlange zum Weibe: Ihr werdet keineswegs des Todes sterben, sondern Gott weiß: an dem Tage, da ihr davon esset, werden eure Augen aufgetan, und ihr werdet sein wie Gott und wissen [...]." (Genesis 2,8 und 3,1)
	"Eine Schlange schlängelt sich so durch's Leben, ihr natürlicher Lebensraum ist an der Aldi-Kasse [...] Und eigentlich ist sie eine verdammt arme Kreatur, denn sie hat so gar keine Beine. Und Arme fehlen ihr auch, der Armen." (zitiert nach )
	"Als ich sechs Jahre alt war, sah ich einmal in einem Buch über den Urwald, das »Erlebte Geschichten« hieß, ein prächtiges Bild. Es stellte eine Riesenschlange dar, wie sie ein Raubtier verschlang. In dem Buche hieß es: »Die Boas verschlingen ihre Beute als Ganzes, ohne sie zu zerbeißen. Daraufhin können sie sich nicht mehr rühren und schlafen sechs Monate, um zu verdauen.« Ich habe damals viel über die Abenteuer des Dschungels nachgedacht, und ich vollendete mit einem Farbstift meine erste Zeichnung. Meine Zeichnung Nr. 1. So sah sie aus: Ich habe den großen Leuten mein Meisterwerk gezeigt und sie gefragt, ob ihnen meine Zeichnung nicht Angst mache. Sie haben geantwortet: »Warum sollten wir vor einem Hut Angst haben?« Meine Zeichnung stellte aber keinen Hut dar. Sie stellte eine Riesenschlange dar, die einen Elefanten verdaut. Ich habe dann das Innere der Boa gezeichnet, um es den großen Leuten deutlich zu machen. Sie brauchen ja immer Erklärungen. Hier meine Zeichnung Nr. 2: Die großen Leute haben mir geraten, mit den Zeichnungen von offenen oder geschlossenen Riesenschlangen aufzuhören und mich mehr für Geographie, Geschichte, Rechnen und Grammatik zu interessieren. So kam es daß ich eine großartige Laufbahn, die eines Malers nämlich, bereits im Alter von sechs Jahren aufgab. Der Mißerfolg meiner Zeichnungen Nr. 1 und Nr. 2 hatte mir den Mut genommen. Die großen Leute verstehen nie etwas von selbst, und für die Kinder ist es zu anstrengend, ihnen immer und immer wieder erklären zu müssen ."

"Die großen Leute haben mir geraten, mit den Zeichnungen von offenen oder geschlossenen Riesenschlangen aufzuhören und mich mehr für Geographie, Geschichte, Rechnen und Grammatik zu interessieren."

für mich ist

• einerseits das "Hantieren" mit Schlangen,
• andererseits "Rechnen" (also "richtige" [???] Mathematik)

kein Widerspruch, sondern Mathematik heißt eben

• nicht nur rechnen,
• sondern auch, anschauliche "Archetypen" entwickeln bzw. mit einbeziehen.

... womit ich natürlich auf die Archetypen-Idee C.G. Jungs anspiele

(und man muss ja nicht an "die" Psychoanalyse bzw. all ihre Ausläufer glauben, um doch immerhin diese Idee in Erwägung ziehen zu können):

Ar|che|typ [auch: ar...; gr.-lat.; "zuerst geprägt; Urbild"] der; -s, -en u. Archetypus der; -, ...pen: 1. Urbild, Urform. 2. Komponente des kollektiven Unbewußten im Menschen, die die ererbte Grundlage der Persönlichkeitsstruktur bildet (C. G. Jung; Psychol.). [...]
(Duden Herkunftlexikon)

Und einer dieser Archetypen scheint eben die Schlange zu sein

(vgl.

"Schlange, ein Symboltier von größter Zwiespältigkeit in der Wertung. In vielen archaischen Kulturen wird sie als Symbol der Unterwelt und des Totenreiches aufgefaßt, wohl wegen ihrer Lebensweise im Verborgenen und in Erdlöchern, zugleich aber auch wegen ihrer Fähigkeit, sich durch Häutung scheinbar zu verjüngen. [...] Tod und Leben sind in dieser Tiergestalt auf so einzigartige Weise symbolisch angedeutet, daß es kaum Kulturen gibt, die der Schlange keine Beachtung geschenkt hätten. [...]"
[Lexikon der Symbole: Schlange. Knaurs Lexikon der Symbole, S. 935]).

Diese Schlange mag viele mythologische Bedeutungen haben (z.B. auch gespaltene Zunge/Falschheit), aber manchmal ist sie vielleicht auch "nur" ein Ordnungsmuster

(vgl. auch das Ordnungsmuster "Symmetrie").

Die ist vor allem ein idealer Handschmeichler und eine wunderschön suggestive Herausforderung zu spielerischen Erkundungen: ich habe noch keinen (auch Erwachsenen) erlebt, der nicht sofort ihre faszinierend elegant-fließenden Bewegungsmöglichkeiten ausprobiert hat

(und einige wollen dann auch prompt das Konstruktionsprinzip herausfinden; s.u.).

Die ist aber außerdem ein in vielfacher Hinsicht äußerst hilfreiches Bild in der Mathematik:

1. im Hinblick auf den Funktionenbegriff, nämlich denn die Schlange ist der Inbegriff von "Differenzierbarkeit" (keine Knicke) und "Stetigkeit" (keine Sprünge)

... wobei gerade die Grenzen und Besonderheiten des Modells interessant sind:

• Angenommen, wir haben keine Schlange, sondern einen

Regenwurm:

entwickelt sich, wenn man ihn bösartig "unstetig" macht, also durchschneidet, aus beiden Enden wieder ein jeweils neuer, vollständiger ("stetiger") Regenwurm?

• Wenn die Schlange sich so

oder so

schlängelt, liegen zwar keine Funktionen mehr vor, aber ergeben sich doch gleich andere hochinteressante Fragestellungen

(Nicht-Funktionen, um das Charakteristische an Funktionen besser zu lernen):

1. die Kreisgleichungen:

"Koordinatengleichung

[...] Der Kreis mit dem Mittelpunkt M( x_M | y_M ) und dem Radius r lässt sich (in der Ebene) wie folgt durch eine Koordinatengleichung ausdrücken:

(x − x_M)² + (y − y_M)² = r²

Diese allgemeine Kreisgleichung ergibt sich unmittelbar aus der Kreisdefinition (siehe oben) und dem Satz des Pythagoras. x und y sind die Koordinaten eines beliebigen Punktes auf dem Kreis.

Ein wichtiger Spezialfall ist die Koordinatengleichung des Einheitskreises:

x² + y² = 1.

Funktionsgleichung

Da der Kreis kein Funktionsgraph ist, lässt er sich auch nicht durch eine Funktionsgleichung darstellen. Behelfsweise kann ein Paar von Funktionsgleichungen verwendet werden:

für den Einheitskreis vereinfacht sich dieses zu

(zitiert nach )

2. "Eine Lemniskate ist die Figur einer liegenden 8 (∞). Diese Figur ist als Symbol für Unendlichkeit und Unbegrenztheit bekannt. Mit dem Begriff »Lemniskate« wird jedoch meist nicht das Unendlichkeitssymbol, sondern eine geometrisch definierte Lemniskatenkurve bezeichnet. Die bekannteste dieser Kurven ist die Lemniskate des Bernoulli.

   

   Gleichungen der Lemniskate des Bernoulli

   • Kartesische Koordinaten:
   • Polarkoordinaten:
   • Parametergleichung: "

   (zitiert nach )

(Nebenbei: "Das Symbol [nämlich ∞ ] selbst steht für einen unendlichen Prozess, vielleicht eine Schlange [!], die sich selbst verschlingt."
[zitiert nach Leonard M. Wapner: Aus 1 mach 2; Wie Mathematiker Kugeln verdoppeln; Spektrum])

Und diese "Lemniskate" schreit ja wiederum nach dem

Möbiusband.

 

• Speziell die Holzschlange ist

(anders als eine richtige Schlange)

eben nicht vollständig "glatt", also differenzierbar, sondern besteht aus kleinen linearen Stückchen:

(woran man auch ansatzweise auch das Konstruktionsprinzip erkennen kann:
beidseitig an ein schmales Gewebemittelband sind kleine Stückchen angesetzt,
zwischen denen kleine Lücken sind, damit die Schlange biegbar ist)

Aber auch in dieser "Stückelung" kann man einen Vorteil sehen, nämlich eine "Propädeutik" der Infinitesimalrechnung, deren Geniestreich ja gerade darauf hinausläuft, mit immer kleinerer linearen Stückchen zu hantieren!

2. weitere "Anwendungsgebiete" von Schlangen:

• Sinus, Cosinus,
• ,
• 
  
• 

Am interessantesten ist die Schlange natürlich in Bewegung, und dabei fasziniert mich am meisten folgender Effekt: es gibt eine (einzige!) bestimmte Art, die Schlange kontinuierlich umzubiegen:

Meine Hände können diesen Effekt problemlos herstellen, aber mir fehlen die Worte, ihn genau zu beschreiben (vgl. ).

Nur soviel ist allerdings klar: weil die Schlange andauernd stramm gespannt ist, besteht sie jeweils aus Teilen von Kreisbögen.

Und damit wird's dann schon ein wenig deutlicher, wie der Effekt funktioniert:

Es ist also ein Tanz von Kreisen umeinander, wobei ab und zu einer auf der einen Seite verschwindet und auf der anderen wieder auftaucht:

Oder vielleicht noch deutlicher mit Zahnrädern:

Und wenn man hier die Bilder nacheinander stehen lässt, erkennt man auch halbwegs, wie die Kreise bzw. Zahnräder sich (auch im Verhältnis zueinander) bewegen, nämlich

• zeitweise parallel nach links oben,
• kurz parallel nach links unten:

Unbefriedigend bleibt aber, dass ich  damit noch immer keine klare mathematische Regel für diese Bewegungen gefunden habe.

Wenn wir uns aber nochmals

anschauen, so wird daran immerhin zweierlei deutlich:

1. stoßen zwei Kreise aneinander, wo ein Wendepunkt der Schlange von einer Links- in eine Rechtskurve bzw. umgekehrt besteht,
2. entsteht ein neuer Kreis auf der anderen Seite, wenn ein erneuter Wendepunkt der Schlange entsteht.

Damit das Schlangenbild auch ja hübsch hängen bleibt und somit allzeit mathematisch nutzbar ist:

(Rubens: Das Haupt der Medusa)

Und um jetzt alles prompt wieder zu vergessen:

in der griechischen Antike war die Schlange das Symbol der Lethe, also des Flusses in der Unterwelt, aus dem die Verstorbenen das Wasser des Vergessens trinken.

Außer den Schlangen gibt es natürlich auch noch andere mathematisch hilfreiche Archetypen bzw. Ordnungs- und Strukturmuster:

• Spiegel

  (
    genauso wie Kongruenzabbildungen oder das Kommutativgesetz),

• Waagen (Gleichungslehre inkl. Termumformungen),
• Spiralen (vgl.  )
• Heinzelmännchen (Variable),
• Lokomotivengestänge (Sinus und Cosinus),
• Propeller (ganzrationale Funktionen ungeraden Grades, aber auch Tangens und Cotangens),
• Brücken (Parabeln),
• Scheibenwischer (Scherung),
• Scheinwerfer oder ein Kopierer, mit dem man vergrößern und verkleinern kann (Streckung, Strahlensätze),
• "Stacheliges" (vgl. und )
• Bergwanderungen (Funktionsverläufe)
  
• 
  
• 
  
• 
  
• und
  
• die Rotation:
  
• "Blüten" in
  
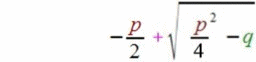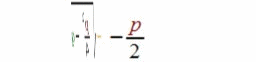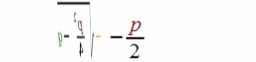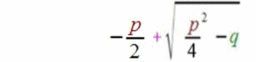
• vgl.
  
  
• ...

(Am interessantesten sind dabei all jene "Strukturmodelle", die [wie pars pro toto Spiegel] mehrfach verwendbar sind, und ich behaupte mal, dass sie es potentiell alle sind

[das ja eben macht Mathematik aus: dass Ihre Erkenntnisse "mehrfach verwendbar" sind; vgl. ):

Und am besten sind die "Strukturmodelle" natürlich in Bewegung: beispielsweise ist eine sich "schlängelnde" Schlange nicht nur staunenswerter, sondern auch - etwa im Hinblick auf den Funktionsgraphenverlauf beim Sinus - aussagekräftiger als eine starre [tote]; vgl. .)

Hilfreich ist dabei zweierlei:

1. das, was kleine Kinder als einzige Spielzeuge brauchen, nämlich massenhaft "Küchenutensilien"

(und die sollten reichlich in   vorhanden sein!),

2. die (zu übende) Fähigkeit, diese Utensilien jederzeit erkenntnisleitend in der Mathematik parat zu haben.

Vgl. "Anschauung statt Anwendung".

Ich versuche hier also, ein wenig bei autistischen Rechenkünstlern abzukupfern

(... wobei reines Rechnen noch lange keine Mathematik ist!):

"[...] Der Brite Daniel Tammet, 28, rechnet präzise wie eine Maschine, und er muss sich nicht einmal anstrengen. Der Mann wartet einfach, bis in seinem Kopf die Lösung erscheint. Eine bunte Landschaft hat er da vor Augen, ein surreales Flirren und Blitzen, in dein er allerlei Zahlen erkennt. Von dieser inneren Szene liest Tammet das Ergebnis ab wie andere Leute von ihrem Taschenrechner.
Immer schon hatte der Rechenmeister Zahlen im Kopf, und sie erschienen ihm in vielerlei Gestalt. „Die 9 ist groß und dunkelblau", sagt er, „die 5 ein Donnerschlag, die 87 wie fallender Schnee."
Wenn Tammet mit seinen Zahlen rechnet, geraten die wundersamen Lichtspiele in Bewegung. Die Bilder zerfließen, kreiseln ineinander, formen sich um und erstarren am Ende zum Resultat, meist begleitet von einem gewissen Britzelgefühl.
Tarnmet hat ein Buch geschrieben über seine Begabung und das Theater der Zahlen in seinem Kopf (am 20. August [2007] erscheint es im Patmos-Verlag auf Deutsch [ ]). Der Titel: „Born on a Blue Day", geboren an einem blauen Tag. Es war ein Mittwoch, als Tammets Mutter den kleinen Daniel bekam, von neun Kindern ihr erstes, das fortan schier unablässig schrie. Und der Mittwoch ist für Tammet eindeutig blau.
Daniel Tammet ist, was Forscher einen Synästhetiker nennen. Menschen seines Schlages sehen Farben, wenn sie an Zahlen oder Daten denken; andere hören Töne dabei. Es gibt auch welche, die ein herzhaft gewürztes Huhn automatisch als spitz empfinden. Bei Synästhetikern sprechen Sinnesbereiche, die sonst getrennt sind, auf einzelne Reize gemeinsam an.
In milder Form kennt diesen Übersprung in der Wahrnehmung jeder. Auch prosaische Menschen sprechen von schreienden Farbtönen, einem scharfen Käse, einem süßen Blick.
[...]"
(zitiert nach )

Und so synästhetisch erlebe ich ja manchmal auch Musik, nämlich mit einem Bilder-Bombardement. überhaupt glaube ich, dass man z.B. auch Gedichte nur "verstehen" kann, wenn sie gleichzeitig auch Musik (Rhythmus, Lautmalerei, Alliterationen ...) und Bildergalerien sind.

Ein erhellendes Beispiel für Ordnungsmuster/Archetypen sind einige "Begebenheiten" um den Physik-Nobelpreisträger Wolfgang Pauli, der sich sozusagen aus beruflichen und privaten Gründen ausgiebig mit der Psychoanalyse Jungs beschäftigt hat, lange Zeit in Behandlung durch Jung-"Schülerinnen" stand sowie einen ausgiebigen Briefwechsel mit Jung geführt hat. Insbesondere ging es da um eine ganze Traumserie Paulis.

(Nebenbei: viele Deutungen dieser Träume durch Pauli selbst, aber auch durch Jung bleiben mir fremd; und überhaupt ist Paulis wissenschaftliche Leistung bis heute hoch anerkannt, während viele Wissenschaftler über seine "psychoanalytischen Ausflüge" dezent hinwegsehen):

• "beruflich", weil die Quantentheorie, die Pauli maßgeblich mitentwickelt hatte, massiv den Beobachter wieder einbezieht und der nunmal ein psychisches Wesen ist

(die erkenntnistheoretischen Banausen unter den Neurobiologen hingegen erklären - u.a. mangels Kenntnis der Quantentheorie! - inzwischen die Psyche wieder als reine Ausdrucksform der Physik);

• "privat", weil Pauli nach einer schweren Lebenskrise Hilfe bei Jung gesucht hat.

In der Physik ergibt sich immer wieder die Frage nach der (einer sehr abstrakten) Symmetrie, und insbesondere beim Beta-Zerfall war das lange Zeit ein Problem.

(Pauli hatte erkannt, dass beim Beta-Zerfall ein bis dahin unbekanntes Elementarteilchen, nämlich das Neutrino, zustande kommen müsste, das dann auch kurze Zeit später nachgewiesen.)

Pauli war immer der festen überzeugung, dass auch der Beta-Zerfall "symmetrisch" sei. Als dann - welche Ironie! - 1957 in den USA nachgewiesen wurde, dass der Beta-Zerfall doch nicht symmetrisch ist, fand Pauli zweierlei bemerkenswert:

1. , dass er sich zufällig wenige Jahre vorher in das Symmetriethema gestürzt hatte

(zufällig?; anscheinend stand es ja gerade an, nämlich auch für die amerikanischen PhysikerInnen),

2. , dass seiner eigenen wissenschaftlichen Beschäftigung mit der Symmetrie Träume vorausgegangen waren, die von Symmetrie handelten, ja, dass überhaupt erst aus diesen Träumen das Bedürfnis entstanden sei, sich auch mathematisch-physikalisch mit Symmetrie zu beschäftigen.

(Hier kann man sich natürlich fragen, was eher war, das Ei oder die Henne: sind Paulis allemal schon vorher vorhandenen naturwissenschaftlichen Kenntnisse zur Symmetrie ihm dann eben auch in die Träume gerutscht?)

Dass die von Pauli erwartete Symmetrie dann doch widerlegt wurde, könnte man als (wichtigen!) Hinweis darauf verstehen, dass Archetypen

(wenn es denn überhaupt welche sind)

manchmal erkenntnisfördernd, manchmal aber auch erkenntnisbehindernd sein können. Vgl. etwa die archetypischen (?) Kreise Platos, die bis hin zu Kepler verhindert haben, dass man die Planetenbewegung einfach (?), nämlich durch Ellipsen, erklären konnte.

Aber gab es überhaupt Alternativen?: bis zur Widerlegung der Symmetrie des Beta-Zerfalls sah die Welt (also auch ohne Archetypen bemühen zu müssen) doch tatsächlich ausnahmslos symmetrisch aus, und die meisten Planetenellipsen sind doch täuschend kreisähnlich.

PS:

zurück zum "Schlangentext"

PPS:
PPPS:
PPPPS:	Vgl. auch