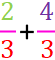 ist besser als 2 :
3 +
4 :
3
ist besser als 2 :
3 +
4 :
3oder
der Vorteil der Bruchschreibweise
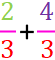 ist besser als 2 :
3 +
4 :
3
ist besser als 2 :
3 +
4 :
3
oder
der Vorteil der
Bruchschreibweise
Zu einem Vorteil der Dezimalzahlen vgl.
![]()
![]()
![]()
Brüche
(nicht zu verwechseln mit der unten genauer erklärten Bruchschreibweise)
haben im Vergleich mit Dezimalzahlen mal Vor-, mal Nachteile:
 wohl 0,5
m einstellen, nicht aber
wohl 0,5
m einstellen, nicht aber
jede „rationale“ Zahl ist
Z.B. ist ![]() =
0,142857 142857 142857 142857 142857 ... = 0,142857. Allerdings
=
0,142857 142857 142857 142857 142857 ... = 0,142857. Allerdings
(wenn man
das ist so selbstverständlich, dass man da nichtmal rechnen muss),
Allerdings können umgekehrt Brüche auch
komplizierter als Dezimalzahlen sein. Z.B. ist der
scheußliche Bruch
 als Dezimalzahl
schlichtweg 3.
als Dezimalzahl
schlichtweg 3.
Ganz nebenbei habe ich eben schon einen ersten, mir seit Ewigkeiten bekannten Vorteil der Bruchschreibweise erwähnt:
(woraus ganz simpel folgt: ).
Damit aber zum zweiten Vorteil der Bruchschreibweise.
(Schade, dass mir dieses Licht erst jetzt aufgegangen ist, denn sonst hätte ich den zweiten Vorteil der Bruchschreibweise während meiner Lehrerzeit auch den Schülern vermitteln und ihnen das Erlernen der Brüche vielleicht vereinfachen können.)
Der Bruchstrich in
![]() bzw.
bzw.
![]() ist nur ein
anderes Zeichen für die Division, d.h. man
könnte genauso gut 2 :
3 bzw.
4 :
3 schreiben, also
ist nur ein
anderes Zeichen für die Division, d.h. man
könnte genauso gut 2 :
3 bzw.
4 :
3 schreiben, also
![]() = 2 :
3 bzw.
= 2 :
3 bzw.
![]() =
4 :
3
=
4 :
3
Der Vorteil der Bruchschreibweise zeigt sich aber erst, wenn man mit mehreren Brüchen rechnen möchte, also z.B.
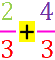 = 2 :
3 +
4 :
3 .
= 2 :
3 +
4 :
3 .
Eine Bruchrechenregel besagt nun:
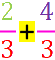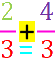 ,
,so dass sich insgesamt
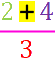 ergibt.
ergibt.
In Kurzform: 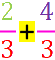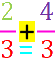 =
= 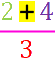 bzw.
bzw.
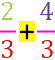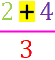 .
.
(Damit ist aus der Addition zweier
Brüche
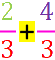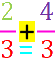 die einfache
Addition 2 +
4 zweier natürlicher Zahlen geworden und
können wir weiterrechnen:
die einfache
Addition 2 +
4 zweier natürlicher Zahlen geworden und
können wir weiterrechnen:
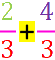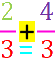 =
=
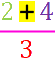 =
=
![]() =
6 :
3 = 2
=
6 :
3 = 2
oder kurz
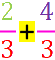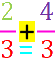 =
2 .
=
2 .
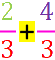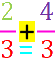 ist also nur eine
ziemlich umständliche Schreibweise für die simple natürliche Zahl
2.)
ist also nur eine
ziemlich umständliche Schreibweise für die simple natürliche Zahl
2.)
Nun sind die Schritte a. und c. aber besonders einfach, wenn
hübsch übersichtlich
direkt nebeneinander
stehen: 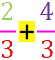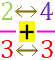
In der alternativen Schreibweise 2 : 3 + 4 : 3 ist dieses übersichtliche Nebeneinander aber nicht gegeben, sondern muss man Umwege gehen, weil nicht zusammenhängende Zahlen im Wege stehen:
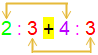
| Das gezeigte Nebeneinander zusammengehöriger Zahlen (der Zähler bzw. der Nenner) bei mehreren Brüchen ist vermutlich der entscheidende Grund gewesen, überhaupt die Bruchschreibweise einzuführen. |
Die Bruchschreibweise ist so schön übersichtlich, dass nur für Brüche Rechenregeln entwickelt wurden, nicht aber z.B. für 2 : 3 + 4 : 3 .
Denselben Vorteil wie bei der Addition hat die Bruchschreibweise auch bei der Subtraktion, Multiplikation und Division.
Eine andere Bruchschreibweise als 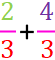 ist 2/3 +
4/3
ist 2/3 +
4/3
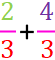 ist aber auch besser als 2/3 +
4/3
, weil bei 2/3 +
4/3 die
zusammenhängenden Zahlen ebenfalls nicht nah
beieinander stehen, sondern man auch hier Umwege
gehen muss:
ist aber auch besser als 2/3 +
4/3
, weil bei 2/3 +
4/3 die
zusammenhängenden Zahlen ebenfalls nicht nah
beieinander stehen, sondern man auch hier Umwege
gehen muss:
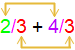
Es gibt allerdings (leider) einen (einzigen) guten Grund, dennoch die Schreibweise
2/3 +
4/3
statt 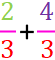 zu benutzen:
zu benutzen:
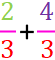 ,
, möglich ist.
möglich ist.