Lernspiralen
echte
Lernspiralen | und | Wissensnetze |
| Warum ins Übertragene und Virtuelle schweifen, "Wenn alles, was in der Welt geschieht, in das System einiger weniger Naturgesetze gefasst werden kann, dann müssen viele anscheinend verschiedene Erscheinungen miteinander in Beziehung stehen. Und tatsächlich ist die Welt, so wie die Physiker sie sehen, wie ein großes, in sich zusammenhängendes Netzwerk. Angefangen bei dem, was unseren Sinnen unmittelbar zugänglich ist, wird dieses Netzwerk, je weiter wir es verfolgen, immer enger, bis schließlich jeder Faden an einem der [...] großen physikalischen Prinzipien endet.
|
![]() Klarstellung
Klarstellung
![]() Inhalt = Methode
Inhalt = Methode
![]() Spiralen
Spiralen
![]() Netze
Netze
Was hier nicht gemeint ist:
Spiralen als in der Tat höchst interessanter thematischer Exkurs im Mathematikunterricht, vgl.
Johanna Heitzer: Spiralen; ein Kapitel phänomenaler Mathematik; Klett
und schon gar nicht gruppendynamischer "Ringelpiez mit Anfassen"
(die Methode nur um der Methode willen, und Hauptsache, wir fühlen uns im Matheunterricht alle ungemein wohl),
wie er letztens auf einer Tagung ernsthaft auch für den Mathematikunterricht vorgeschlagen wurde:
FRIEDENSNETZ
Wir knüpfen aufeinander zu,
wir knüpfen aneinander,
wir knüpfen miteinander,
Schalom, ein Friedensnetz.
Wir knüpfen aufeinander zu,
wir knüpfen aneinander,
wir knüpfen miteinander,
Schalom, eine Friedensnetz.
(nunja, Jugendliche dürfen das, sie brauchen solche Harmonieseligkeit)
Sondern:
|
| Auch wenn man es nicht immer so leicht übertragen kann, sollte man es vielleicht dennoch probeweise zum Kriterium einer sinnvollen Methode machen, dass
|
Um es an o.g. Beispiel klar zu machen:
 ist - und deshalb ein Spiralcurriculum nötig wäre
ist - und deshalb ein Spiralcurriculum nötig wäreDie erste Frage muss also sein, ob der Inhalt der (Schul-)Mathematik spiral- bzw. netzförmig ist.
Mir aber scheint, es gibt überhaupt kein anderes Fach, das so netzförmig ist wie die Mathematik
(mit allen
- Vorteilen, d.h. klarer Logik und Verlässlichkeit,
- Nachteilen, d.h. langweiliger Erwartbarkeit, aber auch gnadenlosem Aufeinanderaufbauen
[wenn man auch nur ein einziges wichtiges Element verpasst hat, hat man später kaum eine Chance mehr bzw. muss zumindest hart nacharbeiten].)
Die ![]() "mathematische Strenge" besagt ja
"mathematische Strenge" besagt ja
(wenn man jetzt mal von erkenntnistheoretischen Problemen absieht, die es durchaus auch in der Mathematik gibt),
dass die gesamte Mathematik über vorher lückenlos bewiesene Zwischenschritte aus den wenigen unzweifelhaften (aber auch unbeweisbaren) Anfangspostulaten bzw. -axiomen aufgebaut werden soll, so dass sich etwa folgendes mathematisches Gebäude ergibt:
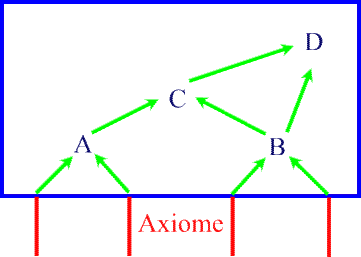
Unter der Voraussetzung, dass die Zwischenschritte tatsächlich lückenlos und logisch sind, ist dieses mathematische Gebäude also sozusagen "unkaputtbar" und "atombombensicher".
(Dabei sei hier mal das Problem weggelassen, dass die Fundamente, also Axiome wackeln könnten bzw. dass, wers aufs Gesamtgebäude abgesehen hat, am besten Sprengsätze an den Fundamenten anbringe, wie es ja beispielsweise auch Lobatschewski und Riemann mit ihrer nichteuklidischen Geometrie getan haben, indem sie das Parallelenaxiom weggesprengt und ohne es eine ganz neue [Parallel-]Mathematik aufgebaut haben, die erst Felix Klein wieder in eine Gesamtmathematik einbauen konnte.)
Während in der Illustration der Einfachheit halber nur vier mathematische Fakten gezeigt wurden (A, B, C und D), sind es in Wirklichkeit natürlich zigtausende, wobei - sobald sie bewiesen sind - ausnahmslos alle über Zwischenschritte auf die untersten Wurzeln rückführbar sind.
(Isolierte Fakten, die noch nicht auf vorher bewiesene und letztlich auf die Fundamente zurückführbar sind, sind bislang nur Vermutungen.
Und wirklich interessant wirds erst bei Gödel, der - vereinfacht gesagt - bewiesen hat, dass es mathematische Fakten gibt, die man [innerhalb des Gebäudes] niemals wird beweisen können, die aber dennoch richtig sein können, denen man aber - so Alan Turing - vor einem eventuellen Beweis auch nicht ansehen kann, ob sie überhaupt beweisbar sind.)
| Die Illustration zeigt also, dass die Mathematik "von Natur aus" und in ihrem Innersten netzförmig, also im Grunde ein großer Text (denn lat. textum = Gewebe) ist (und Teil eines viel umfassenderen Kultur- bzw. Wissensnetzes). |
Interessant dabei ist, dass sich - wie alle Wissensgebiete heutzutage - auch die Mathematik innerlich immer mehr in Spezialgebiete aufspaltet, die derart weit voneinander entfernt liegen (deren gemeinsame Wurzeln derart weit zurück liegen), dass wohl kaum jemand mehr einen Gesamtüberblick hat.
Es ist mal behauptet worden, der Mathematiker Jules Henri Poincaré (1845 - 1912) sei der letzte gewesen, der noch grade einen Gesamtüberblick über die seitdem maßlos explodierende Mathematik gehabt habe.
Um so erstaunlicher
(oder doch aufgrund der gemeinsamen Fundamente gar nicht so erstaunlich?)
ist es, dass
ab und zu auch weit entfernte Zweige der Mathematik einander befruchten können, d.h.
auf dem einen Gebiet erkannte Tatsachen mittels gewisser Grundprinzipien auch auf ein anderes, scheinbar sehr fernes Gebiet übertragbar sein können
(vgl. ![]() ),
),
eben doch einige Grundprinzipien (rote Fäden) die Gesamtmathematik durchziehen
(ein - wenn auch außerschulisches - Beispiel ist da die "Gruppen"-Theorie).
| Die Mathematik ist zudem "von Natur aus" nicht nur netz-, sondern auch spiralförmig |
(und das eben keineswegs nur für angeblich begriffsstutzige SchülerInnen,
denen man alles doppelt und dreifach erzählen,
und wozu man außerdem aufgrund totaler Vergesslichkeit andauernd bei Adam und Eva ganz von vorne anfangen muss).
In der Illustration oben war das bei der Herleitung von Punkt D angedeutet worden, wozu man
nicht nur auf Punkt C eine Ebene tiefer,
sondern sogar ganz nach unten auf A zurückgreifen muss:
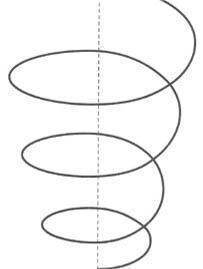 | D C A |
Viele spätere (weiter oben liegende) Fakten bauen auf viel Früherem auf, und zudem wird der Baum/die Spirale nach oben hin immer breiter.
Die Mathematik befindet sich also genauso in (kultureller) Evolution wie auch Lebewesen, die sich immer weiter ausdifferenzieren, aufeinander aufbauen und parallel existieren.
| Da also der Gegenstand (die Mathematik) ein Netz bzw. eine Spirale ist, liegt es nahe, ja scheint es nur folgerichtig, auch die Methode netz- bzw. spiralförmig aufzubauen. |
Dafür scheint es noch einen anderen Grund zu geben: wie beispielsweise Alexander R. Lurija in

gezeigt hat, scheinen sogenannte "Gedächtniskünstler" ein "ganz einfaches" (?) Mittel für ihre Gedächtnisleistungen zu haben: sie ordnen die Einzelfakten wortwörtlich in imaginäre Räume (beispielsweise auch die Geschichte eines Spaziergangs) ein, die sie dann "nur" noch (beispielsweise auch in einer freien Rede) abzugehen haben. Man könnte auch sagen, dass ihnen die Fakten nicht äußerlich bleiben (nur kurzfristig auf Prüfung hin eingepaukt, aber letztlich zum einen Ohr rein, zum anderen raus), sondern dass sich diese "Gedächtniskünstler" mitten in den Dingen bewegen.
| Die Mathematik scheint mir viel eher für jahrgangsübergreifende Großspiralen bzw. -netze als für kleine |
Der gesamte Kanon der Schulmathematik wäre dringendst nach folgenden Kriterien zu durchforsten - und radikal auszumisten!:
Was ist innermathematisch nötig, d.h.
führt zu einer für die Mathematik bezeichnenden (Einzel-)Erkenntnis,
wird später noch mal gebraucht:
nur sporadisch oder sogar ein einziges Mal,
mehrfach oder sogar immer wieder,
ist Teil eines wichtigen, immer wieder auftauchenden roten Fadens?
Was wird außermathematisch (in anderen Fächern und evtl. auch späteren Anwendungsberufen) gebraucht?
(also die angeblich ach so wichtige Prozentrechnung und der ebenfalls ganz ungemein bedeutsame Dreisatz?)
Wer A sagt (was nötig ist), muss auch B sagen (was zugunsten von A weggelassen werden kann - und muss!).
(Um gleich "Butter bei de Fische" zu geben, z.B.
im Zeitalter des Taschenrechners weitgehend die Logarithmenrechnung.)
(Das ist genauso wie mit den derzeit explodierenden neuen Arbeitsbelastungen für LehrerInnen: solche einzuführen hat überhaupt nur ein Recht, wer auch sagt, wo er konkrete und gleichwertige Entlastungen [von bisherigen Tätigkeiten] durchsetzt.)
Im Folgenden soll es mir nur um 1., also das innermathematisch Notwendige gehen.
Hier wäre wohl zu differenzieren nach
dem mathematisch wirklich Bezeichnenden, d.h. den Stoffen, die zentrale mathematische Ideen bzw. ![]() Denkweisen verdeutlichen,
Denkweisen verdeutlichen,
den (dafür) nunmal unabdingbaren Techniken.
Nur diese Dinge (oben 1c) sollten - wenn überhaupt - von der Kultusbürokratie bzw. Fachkonferenzen verpflichtend gemacht werden, was u.a. hieße, die ellenlangen Rahmenrichtlinien auf wenige Seiten (und ganz wenige Punkte pro Schuljahr) "einzudampfen".
Zweifelsohne muss es gerade dann, wenn man eine - wie unten angedeutet - jahrgangsübergreifende Spirale aufmachen will, aber zumindest schulintern einen Minimalkonsens geben. Um es nur an einem einzigen Punkt zu verdeutlichen:
wenn man den Satz des Pythagoras als wichtig genug ansieht, ihn mit einem Stammplatz in der Spirale zu beehren, dann muss sich einE nachfolgendeR LehrerIn z.B. der Oberstufe auch darauf verlassen können, dass ihre/sein VorgängerIn ihn auch tatsächlich gründlich in der 9. Klasse durchleuchtet hat.
All das heißt gerade nicht, dass andere Punkte verboten wären. Sondern im Gegenteil eröffnen sich da vielfältige Möglichkeiten für Exkurse (siehe 1a) und Projekte:
| etwas bislang schier Undenkbares müsste ermöglicht werden: die MathematiklehrerInnen erhalten Entscheidungsspielraum, und man traut ihnen "eigenverantwortliches" Handeln (im Hinblick auf die Mathematikspirale) zu. |
Wichtig ist noch die Unterscheidung zwischen dem, was (s.o. unter 1.)
später nur sporadisch oder sogar ein einziges Mal,
mehrfach oder sogar immer wieder
gebraucht wird.
Angenommen mal, man braucht den Strahlensatz Jahre später nur noch ein einziges Mal (und dann auch nur sehr kurz) bei der Einführung der trigonometrischen Funktionen. Unter dieser vielleicht zweifelhaften, aber doch gängigen Voraussetzung gehört er nicht in die eigentliche Spirale, sollte man also auch nicht darauf vertrauen bzw. gar vorwurfsvoll bestehen, dass die SchülerInnen ihn noch erkennen und beherrschen, sondern einfach nur kurz nachschlagen.
Es darf eben nicht alles, was irgendwann (vor Jahren) mal da war, seitdem aber nie wieder benutzt wurde, als selbstverständlich vorausgesetzt werden - wie es beispielsweise in Parallelklausuren in der 10. Klasse passiert, wenn da urplötzlich wieder die ach so wichtige Prozentrechnung auftaucht, die seit Jahren nicht wieder durchgenommen bzw. benutzt wurde.
| Wenn etwas aber wichtig genug erscheint, in der Spirale aufzutauchen, dann wird Vorsorge getroffen werden müssen, dass es tatsächlich immer wieder (unscheinbar und variiert) auftaucht. |
Im Folgenden sehe ich mal von allen technischen Schwierigkeiten ab, also z.B.
wie eigentlich baut man eine metergroße Spirale, wo nimmt man sie her?
(was ja immerhin mal Anlass wäre, Spiralen zum mathematischen Thema zu machen und - wie ein Kollege es mal an meiner Schule gemacht hat - sie selbst zu bauen)
Klassenraumwechsel und (insbesondere in der Oberstufe) Neuzusammensetzung von Klassen und Kursen,
leichtfertiger bis geradezu grob zerstörerischer Umgang der SchülerInnen mit der spirale und dem Netz
(vermutlich insbesondere dann, wenn der Klassenraum auch von anderen Klassen/Kursen benutzt wird, die nicht - wie die Originalklasse - ihr "Herzblut" in die Spirale bzw. das Netz investiert und deren Wert erkannt haben).
Solche Schwierigkeiten lassen sich gewiss überwinden - wenn man nur will.
Zudem könnte beispielsweise ein Klassenraumwechsel oder die Neuzusammensetzung eines Kurses ja sogar eine Chance sein: dann fängt man halt mit der (sukzessiven) Rekonstruktion einer Spirale oder eines Netzes an, was ja immerhin eine schöne strukturierende Wiederholung und Selbstvergewisserung wäre.
Es wäre also durchaus denkbar, dass eine große Spirale (evtl. sogar mit Jahrgangsbezeichnungen versehen) wie ein Tannebaum in der Klassenraumecke steht
und daran immer wieder mittels Fäden Verbindungen quer über die "Stockwerke" vorgenommen werden (s.u. bei den Netzen).
Allerdings sollte (wie im Folgenden die Netze) die Spirale wohl eher langsam "mitwachsen", damit sie für einen Anfänger nicht frustrierend endlos erscheint (mit dem allzu vagen Versprechen von oftmals verschwindend geringem oder völlig verstelltem "Licht am Ende des Tunnels").
| Wichtig (auch bei Netzen) ist, dass
|
scheinen mir nun doch sinnvoller und praktikabler als Spiralen.
Dabei ist heute wohl dringend darauf hinzuweisen:
"Vernetzung" (hier nicht von Computern, sondern des Wissens) ist zu einer Floskel verkommen ist, die etwa gleichbedeutend mit "Ganzheitlichkeit" ist:
"alles hängt irgendwie, irgendwo, irgendwann mit allem zusammen,
aber nix Genaueres weiß man nicht".Um so notwendiger ist es, das "Netz" wieder - wie hier - wortwörtlich zu verstehen und zu gestalten.
Oftmals wird ja tatsächlich in geradezu religiösen Tönen eine soziale und geistige Vernetzung mittels des "www", also "World Wide Web" = "Weltweites Netz" = Internet prophezeit. Mir scheint da - schon allein aufgrund der Masse - hingegen nur (kreatives?) Chaos zu herrschen: unter einem Netz versteht man ja kaum eine wüste, unentwirrbare Ansammlung von losen Fäden, sondern eine überschaubare Anordnung:
es sollten zumindest klare Substrukturen erkennbar bzw. - ggf. mit einiger Mühe - herauszuarbeiten sein (z.B. einerseits die Längs-, andererseits die Querverbindungen),
die dann allerdings untrennbar zu einem Größeren verbunden sind (kein Netz nur aus Längs- bzw. nur aus Querfäden: es bliebe alles nur eindimensional, erst die Verbindung von Längs- und Querfäden ergibt das zweidimensionale Netz).
Ein schönes Beispiel für verbundene Substrukturen ist Literatur.
Hier seien kurz stichwortartige Ideen für ein reales Netz im Unterrichtsraum entwickelt:
das Netz schwebt wenig störend und dennoch permanent sichtbar unter der Decke des Klassenraums
(evtl. an einer Reihe von Haken ringsum an allen Wänden),
es wird grundsätzlich von hinten (aus der Vergangenheit) nach vorne (zur Tafel hin, in die Zukunft) aufgebaut
(womit schon eine Hierarchisierung und Nacheinanderordnung des Wissens stattfindet),
es ist dreidimensional, so dass erheblich einfacher als bei ![]() verschiedenartigste Querverbindungen hergestellt werden können,
verschiedenartigste Querverbindungen hergestellt werden können,
evtl. bedarf es eines möglichst unscheinbaren/unsichtbaren Trägernetzes,
das Netz wird niemals vorgegeben, sondern grundsätzlich gemeinsam geplant
(wobei - s.u. - die Lehrkraft ein gewisses Mitsprache- und Vetorecht hat),
zu Beginn der 5. Klasse könnten in einem Rückblick die Erkenntnisse der Grundschule in das Netz eingearbeitet werden, damit die Kontinuität deutlich wird,
überhaupt wäre zu Beginn jeder Klasse ein Rückblick sinnvoll,
das Netz ist nie fertig, sondern wird
immer weiter ausgebaut
(und dazu evtl. verkleinert oder auf die wichtigsten Elemente reduziert),
mit neuen (evtl. nachträglich erkannten) Querverbindungen versehen,
ggf. umsortiert,
überschaubarer angeordnet, wenn es zu unübersichtlich wird,
aussortiert
(eine früher nur scheinbar wichtige Erkenntnis erweist sich im Nachhinein als nebensächlich oder wird durch eine allgemeinere, weiterreichende ersetzt),
beispielsweise in der 5. Klasse kann das Netz in zwei noch unverbundenen Ecken (Algebra, Geometrie) anfangen, die erst nach und nach (z.B. bei der Winkelsumme) zusammenwachsen, ja spätestens etwa bei der Analysis untrennbar bzw. ununterscheidbar geworden sind,
mit besonders starken, verschiedenfarbigen Fäden werden (mit Bezeichnungen versehene!) "rote Fäden" markiert, also z.B. "Zahlbereiche", "Verbindungen Algebra/Geometrie", "Funktionenbegriff" ...
jede Verbindung bzw. jeder Faden ist zu verbalisieren
(dranschreiben!),
die "Knoten" (Einzelfakten) werden mit Schildern versehen, auf denen ihr Name (also z.B. "Assoziativgesetz") steht, evtl. aber auch (etwa in einem Briefumschlag) mit den (Rechen-)Regeln, so dass man jederzeit Vergessenes nachschlagen kann,
denkbar sind auch auffällige Warnschilder bei (bitter selbst gemachten) Standardfehlern oder bedeutsamen Einschränkungen
(z.B. "Pythagoras NUR bei RECHTWINKLIGEN Dreiecken, ansonsten ggf. mittels Höhe in rechtwinklige Dreiecke zerlegen!"),
es können mobileartig Subnetze untergehängt werden
(z.B. zur Satzgruppe des Pythagoras; die geradezu handwerkliche Anfertigung solch eines Subnetzes kann zudem Referatthema für EinzelschülerInnen sein),
manchmal (z.B. beim "Pythagoras") sind auch Illustrationen (Graphen) sinnvoll,
nach Erarbeitung eines Subnetzes muss grundsätzlich wieder "aufgetaucht", müssen also die Details ins Gesamtnetz eingeordnet werden
(vgl. etwa eine Gedichtinterpretation, die bei aller Detailgenauigkeit dennoch mit einem Gesamteindruck enden sollte),
es kann durchaus auch die Zukunft eingehen:
z.B. (etwa in mausgrau) die wichtigsten Fakten einer (wenn auch den SchülerInnen vermutlich noch wenig sagenden) Schuljahrsvorwegplanung,
Fernziel "wir »wollen«alles berechnen können [exakt erhalten], was wir auch zeichnen können [was uns anschaulich ist] - und umgekehrt",
weiterführende Erkenntnisse, die sich schon angedeutet haben
(z.B. das Integrationsverfahren, wenn man die Kreisfläche berechnet hat),
sich im Unterricht ergebende, aber noch nicht auflösbare Desiderate (ausdrückliche Fragen)
(z.B., dass man schon mittels der Winkelsumme drei Winkel und mit der Satzgruppe des Pythagoras drei Seiten, aber - vor den trigonometrischen Funktionen - noch nicht Winkel und Seiten miteinander in Verbindung bringen kann;
oder: wir können zwar schon das Minimum [Scheitelpunkt] einer Funktion zweiten, nicht aber das einer Funktion dritten Grades berechnen),
durchaus auch schon mal Hinweise der Lehrkraft, wo ein derzeitiger Stoff später nochmals wichtig wird bzw. hinführt
("non vitae, sed scholae discimus"; an solchen schon ansatzweise inhaltlich gefüllten statt nur benannten Vorausblicken sind SchülerInnen durchaus interessiert: z.B. konstruieren auch Sechtsklässler schon mal gerne irrationale Zahlen à la 0, 1 0 11 0 111 0 1111 0 ... und sind dann mächtig stolz, wenn man ihnen sagt, dass sie ja "eigentlich" erst Stoff der 9. Klasse;
und solche Vorausblicke sind manchmal durchaus nötig, damit sich bei SchülerInnen nicht Einseitiges oder gar Falsches festsetzt [z.B. "mit den rationalen hat man auch schon alle Zahlen"] und sie sich später nicht reingelegt fühlen ["es gibt doch noch mehr Zahlen"]):
Jeder Unterricht sollte ab und zu derart in seine eigene Zukunft blicken
(z.B. sollten 10-Klässler wissen, was in einem eventuellen Leistungskurs auf sie zukommt - und ob sie das überhaupt interessiert),
Mit solch einem Blick in die Zukunft wird das Netz zu einem erkenntnisleitenden und vielleicht auch motivierenden Forschungsvorhaben!
es sind Inseln (Exkurse), aber auch Beziehungen zu anderen Fächern (z.B. der Physik) einbaubar
(und vielleicht wird sogar einE PhysiklehrerIn zu sowas animiert, wenn sie/er unter solch einem Netz unterrichtet; bzw. zumindest weiß sie/er dann, auf welcher Mathematik sie/er aufbauen kann;
wobei mal dahingestellt sei, dass Physik meist in einem anderen [Fach-]Raum stattfindet),
es wäre durchaus denkbar, Einzelerkenntnisse auch mit den Namen derjenigen SchülerInnen zu versehen, die drauf gekommen sind und nun Anlass zu Stolz haben
(also z.B. "das Gaby-Gesetz"),
es sind ganze Unterrichtsstunden, ja sogar -phasen denkbar und sogar nötig, in denen überhaupt kein neuer Stoff erarbeitet, sondern nur die Konstruktion des Netzes bedacht wird
(und gerade solche Stunden/Phasen wären geeignet für die verbale Kommentierung in ![]() Lerntagebüchern),
Lerntagebüchern),
die Anordnung des Netzes ist also permanenter Diskussionsgegenstand, und überhaupt wird andauernd zurückgeschaut,
insbesondere aktuelle Teile des Gesamtnetzes könnten von SchülerInnen in ![]() umgesetzt bzw. geplant werden,
umgesetzt bzw. geplant werden,
das Netz steht zur permanenten Wiederholung (auch außerhalb der Mathematikstunden) zur Verfügung
("schau doch bitte nochmals in jenen Umschlag!"),
von ganz besonderem Interesse und vielleicht auch großer Motivation sind sich nachträglich ergebende Verbindungen, bei denen die SchülerInnen überhaupt erst bemerken,
wie wichtig eine frühere, damals noch unscheinbare Erkenntnis war
(die sich derart nachträglich legitimiert),
wie einfach sie im Nachhinein erscheint
(obwohl sie seinerzeit enorme Mühe gekostet hat),
wie zusammenhängend und wohlstrukturiert überhaupt der Gesamtstoff der Mathematik ist
(eine zentrale Erkenntnis, die SchülerInnen allerdings oftmals vorenthalten wird, bzw. oftmals sehen sie "vor lauter Bäumen den Wald nicht mehr"),
die Lehrkraft verweist immer wieder auf die einzelnen Knoten, aber auch die Gesamtkonstruktion des Netzes:
jeder Stoff wird da eingehängt,
es wird (zumindest im Nachhinein) immer wieder gefragt, ob und wie ein (neues) Faktum mit alten verbunden werden kann,
weil die Lehrkraft naturgemäß vorausschauender ist (die Folgemathematik kennt), muss sie evtl. auf der Aufnahme gewisser Punkte und deren Einbindung bestehen, auch wenn deren Bedeutung den SchülerInnen noch nicht klar ist/sein kann;
das Netz bleibt naturgemäß und mit Absicht bei Klassenarbeiten zur Orientierung hängen
(evtl. darf nur nicht in aktuelle "Umschläge" geschaut werden),
wie jede allzu lang eingesetzte Methode birgt auch die "Netz-Methode" die Gefahr, dass sie langweilig und damit kontraproduktiv wird, und zwar insbesondere natürlich dann, wenn sie über Jahre hinweg eingesetzt werden soll; woraus nur folgen kann, dass sie zwar immer wie ein Damoklesschwert über einem schwebt, aber doch auch in langen Phasen kaum beachtet wird.
| Insgesamt ist es der Sinn solch eines Netzes, augenfällig zu zeigen:
|
Als Bespiel für ein zu erstellendes Netz sei der "Geometriestammbaum" genannt:
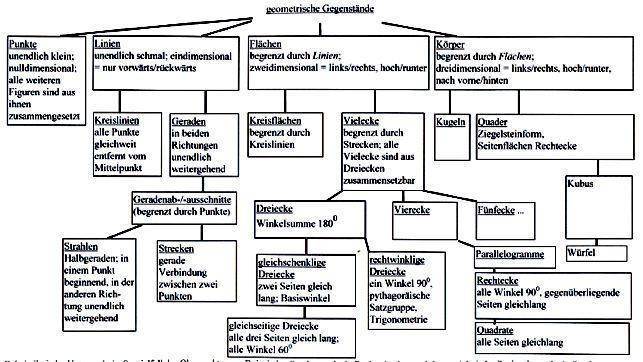
Die Erstellung solcher langfristigen Netze hat nicht nur für SchülerInnen, sondern auch für LehrerInnen Vorteile: letztere haben regelrecht permanent vor Augen,
Vielleicht ein wenig arg dick aufgetragen und damit (immer schon) verdächtig patentrezepthaft:
| Mit der Erstellung des Netzes werden die SchülerInnen zu "Herren" ihres eigenen mathematischen Schicksals, statt dass ihnen immer nur
die (mathematischen) Trümmer vor die Füße knallt ("friss oder stirb"):
|
| Insbesondere - darauf vertraue ich mal - kann solch ein Netz massiv dazu beitragen, dass |