wie man "präsentiert"

"Präsentiiiiiiiiiiiiiiert das Gewehr!"

Vgl. auch

 Was früher "Referat" hieß, heißt heutzutage neumodisch "Präsentation" - und ist auch nicht besser.

(Mit Schrecken denke ich noch an das ungelebte Leben in Pädagogik- und Germanistik-Seminaren während meines Studiums, wo jahrein, jahraus jeweils eine Gruppe gelangweilt ein Referat über ein Thema hielt, von dem kein anderer einen blassen Schimmer hatte - und der Rest im Tiefschlaf versank.)

Der einzige Unterschied ist vielleicht, dass die Medien der "Präsentation" neu sind:

• die geile "Flipchart" ,
• die methodische Weltneuheit

Museumsgang Der Museumsgang (auch: Markt der Möglichkeiten) ist eine Methode, Ergebnisse einer Gruppenarbeit durch Schülerinnen und Schüler sich gegenseitig zu präsentieren.

• und einige Knallköpfe unter den LehrerInneN machen sogar Powerpoint verpflichtend.

Der entscheidende Fehler ist nach wie vor, dass man zu den SchülerInnen

"nächste Woche seid ihr mit der Präsentation / dem Referat dran"

sagt und sie dann allein lässt, also nie erarbeitet wird, wie denn eine - was immer das sei: - gute "Präsentation" aussieht

(mehr noch: oftmals scheinen mir LehrerInnen selbst keine [expliziten] Kriterien für eine gute "Präsentation" zu haben).

Im Folgenden

• geht es an zwei Beispielen nur um die Inhalte von Referaten, nicht um den Vortragsstil,
• soll kurz anhand zweier Themen aus meinem derzeitigen Unterricht überlegt werden, wie "gute" Präsentationen aussehen könnten. Dabei ist das erste Thema ein eher theoretisches (geeignet für ein Standardreferat), das zweite ein eher praktisches (geeignet für Visualisierungen, Modelle ...):

1. In "meinen" elften Klassen lasse ich derzeit nacheinander die 50 Aufsätze aus dem Buch vorstellen, damit die SchülerInnen über den üblichen Unterricht hinaus die wichtigsten Gegenstände und   Denkweisen der Mathematik kennenlernen. Exemplarisch sei hier der Aufsatz über Brüche behandelt

(und weil ich ja Reklame für dieses Buch mache, erlaube ich mir, den Aufsatz komplett zu zitieren):

Fragt sich nur, was daran überhaupt interessant, also mitteilenswert, d.h. eines Referats würdig ist: doch sicherlich nicht die Darstellung, was Brüche überhaupt sind und wie die Bruchenrechenregeln funktionieren. Das weiß doch jedeR SchülerIn, das sind doch olle Kammellen

(was ja nicht ausschließt, dass da in komplizierteren Fällen noch immer Fehler unterlaufen).

Oder ist das schon ein Denkfehler?:

1. : warum denn eigentlich heißt der Zähler "Zähler" und der Nenner "Nenner"?

(Das Erste, was man tut, ist, einen Kuchen in n gleiche Teile aufzuteilen, und diese Teile werden mit "Nenner" benannt; der "Zähler" zählt dann in einem zweiten Schritt, wie viele Teile man davon nimmt; d.h. Brüche werden von unten nach oben gelesen!)  

2. : bemerkenswert an den Bruchrechenregeln ist doch, dass selbst die schlauesten Mathematiker überhaupt nicht direkt mit Brüchen rechnen können, sondern von Glück reden können, dass mit den Bruchrechenregeln die Bruchrechnungen auf simple Rechnungen mit ganzen Zahlen zurückgeführt werden können, also das Einzige, was wir können.

Nun sind die Brüche den SchülerInneN aber wohl allzu selbstverständlich, als dass ihnen 1. und 2. noch auffallen könnten. Da zeigt sich das merkwürdige Paradox:

"Er wusste [nicht] genug, um Fragen stellen zu können."
(Quelle abhanden gekommen)

Bemerkenswert an dem Aufsatz finde ich aber ansonsten "nur":

3. , dass bei den Brüchen die Multiplikation einfacher ist als die Addition,
4. , die merkwürdige Stammbruch-Rechnerei der alten Ägypter,
5. , dass bis heute kein Weg gefunden wurde, die kürzeste Stammbruchentwicklung herauszufinden,
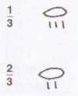6. : liegt da ein Druckfehler vor - oder nach welcher sonderbaren Logik funktioniert das?
7. Erwähnenswert wäre zudem noch, was allerdings nicht in dem vorliegenden Aufsatz, sondern (logischerweise) in dem danach folgt: dass es nämlich auch "irrationale" Zahlen gibt, die nicht als Bruch darstellbar sind und höchst merkwürdige Eigenschaften haben.

Und da könnte man dann auch ergänzen, dass Pythagoras meinte, Gott habe die Welt allein mit ganzen Zahlen und Brüchen aus diesen erschaffen - und dass er angeblich den ersten, der die Existenz irrationaler Zahlen bewies, hat hinrichten lassen!

(Aber das können SchülerInnen ja gar nicht wissen, darauf muss man sie - wie immer Referate begleitend - hinweisen!)

D.h. ich würde in einem Referat nur das vorstellen, was mir bemerkenswert, erstaunlich oder regelrecht dramatisch erscheint, denn nur das dürfte auch die ZuhörerInnen interessieren!

2. In zwei "Differenzierungskursen" nehme ich derzeit

und da speziell

durch.

Bemerkenswert ist da u.a., dass die Würfelverdopplung eben doch möglich ist: zwar nicht mit Zirkel und Lineal, aber erstaunlicherweise mit Origami.

Vorlage für die SchülerInnen ist da

Da aber der Beweis, dass diese Origami-Art der Würfelverdopplung funktioniert, für die SchülerInnen noch zu schwierig ist

(ebenso wie der Beweis, dass die Würfelverdopplung nicht mit Zirkel und Lineal möglich ist),

interessiert an dem Text nur die reine Konstruktion, d.h. er reduziert sich zu

(Dass die Konstruktion den Ausgangswürfel tatsächlich verdoppelt,
müssen die SchülerInnen dann einfach "glauben".)

Ziel des Unterrichts ist es, alles Durchgenommene am Ende des Jahres in einer Ausstellung

(für die gesamte Schule)

zu "präsentieren". Wie aber kann und sollte das am Beispiel der Würfelverdopplung aussehen?

1. müsste das Problem vorweg möglichst "drastisch" erklärt werden:

"Nach einer Legende befragten die Bewohner der Insel Delos während einer Pestepidemie 430 v. Chr. das Orakel von Delphi um Rat. Dort wurden sie aufgefordert, den würfelförmigen Altar im Tempel des Apollon im Volumen zu verdoppeln. Für antike Mathematiker bedeutete dies, dass die Seitenlänge eines Würfels mit dem doppelten Volumen unter ausschließlicher Verwendung von Zirkel und Lineal konstruiert werden sollte."
(zitiert nach )

... was aber doch bedeutet, dass das Orakel die Bewohner von Delos übel reingelegt hat, da sie die Origami-Lösung noch nicht kennen konnten. Bzw. dass vielleicht hunderte von Pestopfern gerettet worden wären, wenn die die Bewohner von Delos die Origami-Lösung gekannt hätten!

(Nebenbei: wo liegt Delos, was an dieser Insel ist bemerkenswert, was genau war das Orakel von Delphi ...?)

Zudem müsste auch erklärt werden, dass gesucht ist.

2. eine Darstellung der "Klassischen Probleme der antiken Mathematik" und ansatzweise ihrer Unlösbarkeit mit Zirkel und Lineal; das impliziert: warum eigentlich die Einschränkung "mit Zirkel und Lineal"?
3. das Staunen "richtiger" Mathematiker, dass die Würfelverdopplung "dennoch" (eben mit Origami) möglich ist: