Heiner Stauff - anschauliche Mathematik

die Gefährlichkeit der Mathematik

... und das Problem ist, dass diese Gefährlichkeit auch und gerade an den unscheinbarsten Stellen lauert, also keineswegs nur in der "Hardcore-Mathematik".

Ein einziges, aber bezeichnendes Beispiel:

gesucht sind die Nullstellen N (x | 0) der doch noch relativ simplen Funktion

f: y = x³ - x,

d.h. es ist gefragt, für welche x

0 = x³ - x

gilt.

(Kurz eingefügt sei, weshalb man überhaupt andauernd Nullstellen

[und Schnittpunkte mit der y-Achse]

berechnet: wenn man mal von Anwendungen absieht

["wann haben die Finanzen eines Unternehmens eine Nullstelle, d.h. wann geht das Unternehmen pleite?"],

so dienen diese wenigen und relativ einfach zu errechnenden Standardpunkte dazu, schnell eine Grundvorstellung vom Funktionsgraphen zu bekommen, denn schließlich kann und will man nicht alle [= unendlich viele] Punkte des Funktionsgraphen berechnen.

Des weiteren seien kurz die Besonderheiten von Nullstellen und Schnittpunkten mit der y-Achse erklärt:

Funktionen können

[müssen aber nicht]

nur einen einzigen Schnittpunkt mit der y-Achse haben

[sonst lägen mehrere solcher Schnittpunkte übereinander und läge somit gar keine Funktion mehr vor],

aber mehrere Nullstellen haben;

zweite Unterscheidung

[und hier liegt eine notorische Verwechslungsgefahr vor]:

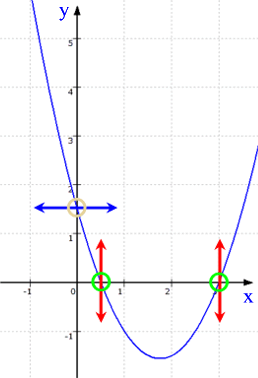beim Schnittpunkt mit der y-Achse ist x = 0,
bei Nullstellen, also Schnittpunkten mit der x-Achse, ist y = 0:

)

Es seien zwei Methoden vorgeführt, mit denen man die Nullstellen der Funktion f: y = x³ - x berechnen kann:

die einfachere, aber gefährlichere Methode:

0 = x³ - x | + x

x = x³ | : x

1 = x² |

1 = x

Die Funktion f: y = x³ - x hat also als einzige Nullstelle N (1 | 0), weshalb ihr Graph

(weil eine Funktion 3. Grades vorliegt)

ungefähr so aussehen muss:

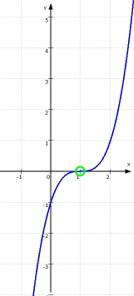
("ungefähr so" bedeutet dabei, dass die Kurve durchaus steiler oder flacher sein kann,
Hauptsache, die [einzige] Nullstelle bleibt erhalten)

die umständlichere, aber letztlich doch wohl gefahrlosere Methode:

0 = x³ - x
0 = (x² - 1 ) • x	(1. Trick: Distributivgesetz)
0 = (x² - 1 ) oder 0 = x	(2. Trick, der nur für die Multiplikation gilt: das Produkt zweier Terme ist genau dann gleich Null, wenn [mindestens] einer der beiden Terme gleich Null ist.)

Die erste erkennbare Nullstelle ist also N (0 | 0). Damit haben wir aber eine andere bzw. zusätzliche Nullstelle gefunden als in 1.,

womit man sich fragen kann, ob 1. oder 2. richtig ist. Um das zu überprüfen, setzen wir x = 1 und x = 0 in die Funktionsgleichung y = x³ - x ein und erhalten

für x = 1 das Ergebnis y = 1³ - 1 = 1 - 1 = 0, d.h. für x = 1 liegt tatsächlich eine Nullstelle vor,

für x = 0 das Ergebnis y = 0³ - 0 = 0 - 0 = 0, d.h. für x = 0 liegt tatsächlich eine Nullstelle vor.

(Nebenbei: dass [wie in 2.] für x = 0 eine Nullstelle vorliegt, hätten wir auch noch anders herausbekommen können: viel einfacher als die Nullstellen ist nämlich der Schnittpunkt S_y (0 | y) mit der y-Achse bestimmbar:

y = 0³ - 0 = 0 - 0 = 0,

d.h. es ergibt sich S_y (0 | 0). Die Funktion geht somit durch den Ursprung und schneidet dort also nicht nur die y-Achse, sondern auch die x-Achse. S_y(0 | y) ist also gleichzeitig auch Nullstelle.

Ebenfalls nebenbei: dass S_y (0 | 0 ) der Schnittpunkt des Funktionsgraphen mit der y-Achse ist, kann man sogar ohne jede Rechnung an der Funktionsgleichung ablesen: der y-Wert von S_y (0 | y) ist immer derjenige Teil des Funktionsterms, in dem kein x vorkommt

[der Teil, der übrig bleibt, wenn man x = 0 einsetzt],

also y = x³ - x + 0. Im vorliegenden Fall hat das allerdings den Nachteil, dass man sich 0 hinzudenken muss.)

Also hat sowohl 1. als auch 2. Recht. Fragt sich nur, weshalb wir

in 1. nur die eine Nullstelle N₁ (1 | 0) ,
in 2. nur die andere Nullstelle N₂ (0 | 0)

erhalten bzw. wieso wir in beiden Fällen die jeweils andere Nullstelle übersehen haben.

Dieses "Übersehen" ist aber das größte Problem: man rechnet (scheinbar) richtig vor sich hin und merkt gar nicht, dass man Lösungen (Nullstellen) verloren hat.

Nun müssen wir aber unterscheiden:

in 1. waren wir mit der Rechnung vollständig fertig, haben wir also in der Tat eine Nullstelle (nämlich N₂ (0 | 0) ) übersehen;

in 2. waren wir mit der Rechnung aber nur halb fertig:

wir hatten uns in 0 = (x² - 1 ) oder 0 = x

nur den zweiten Teil, nämlich 0 = x, angesehen,
aber noch nicht den ersten Teil, also 0 = (x² - 1 ).

Holen wir also Letzteres nach:

a.: 0 = (x² - 1 )

0 = x² - 1 | + 1

1 = x² |

1 = x

Wir erhalten also mit dem "ersten Teil" doch noch

(zusätzlich zur Nullstelle N₂ (0 | 0) , die wir bereits von 0 = x her kannten)

die Nullstelle N₁ (1 | 0), die wir bereits aus 1. kennen.

Es sieht also sehr danach aus, dass

die Rechnung in 1. unvollständig ist

(zwar die eine Nullstelle N₁ (1 | 0) ergibt, aber die andere Nullstelle N₂ (0 | 0) unterschlägt),

die Rechnung in 2.a. hingegen vollständig ist

(beide Nullstellen ergibt).

Mit 2.a. sieht der Funktionsgraph also ungefähr

entweder so oder so
(in jeweils dem einem Punkt ein echter Schnitt mit der x-Achse,
in jeweils dem anderen Punkt eine Berührung der x-Achse)

aus.

Kommen wir damit zu einem zu 2.b. alternativen Verfahren, um in 2. die Teilaufgabe 0 = (x² - 1 ) zu lösen:

Wenn man in (x² - 1 ) den "3. Binomi" (x² - 1 ) = (x - 1) • (x + 1) erkennt, so ergibt sich

0 = (x - 1) • (x + 1)

Da wieder eine Multiplikation vorliegt, können wir auch wieder den 2. Trick von oben anwenden und

0 = (x - 1) oder 0 = (x + 1)

schreiben bzw.

0 = x - 1 oder 0 = x + 1 .

Addition bzw. Subtraktion von 1 auf beiden Seiten der Gleichungen ergibt dann

1 = x oder -1 = x .

Damit erhalten wir

einerseits die zweite, bereits bekannte Nullstelle N₂ (+1 | 0),
andererseits die dritte , bislang übersehene Nullstelle N₃ (-1 | 0).

Mit den inzwischen also bekannten drei Nullstellen N₁ (0 | 0), N₂ (+1 | 0) und N₃ (-1 | 0) sieht unser Funktionsgraph nun also (endgültig!) so aus:

Da stellt sich doch die dringende Frage, wieso wir

beim Verfahren 2.a. eine Nullstelle
und beim Verfahren 1. sogar zwei Nullstellen

übersehen haben.

Der Fehler scheint in 1. und 2.a. derselbe zu sein, da beides Mal dieselbe Rechnung

1 = x² |

1 = x

vorkommt. Erinnern wir uns dazu an die Definition der Wurzelfunktion:

zwar gilt z.B. (-1)² = +1 und (+1)² = +1, d.h. das Quadrat jeder (sei's negativen, sei's positiven Zahl) ist positiv:

um das Quadrieren rückgängig zu machen, benutzt man die Wurzel, und dann ergeben sich
- = -1 und
- = +1 :

Das nun aber ist keine Funktion (kein Funktionsgraph), da hier (mindestens)

(mindestens) einem x (+1)
mehrere (hier zwei) y-Werte (-1 und +1) zugeordnet werden.

Oder anders gesagt: die Wurzel-Abbildung ist nicht eindeutig. Da die MathematikerInnen es nun aber gerne immer hübsch eindeutig (Funktionen) haben wollen, "kastrieren" sie die obige Abbildung und lassen nur den oberen Zweig zu:

Ab sofort ist also

nur noch +1
und nicht mehr auch -1:

wir ziehen aus positiven Zahlen nur noch die positive Wurzel.

Der unbedingte hat nun aber den entscheidenden Nachteil, dass wir eine Lösung, nämlich -1 , verlieren.

Und deshalb muss man nach dem positiven Wurzelziehen eben doch wieder plus und minus hinzufügen, also

+ = + ( +1 ) = +1 ,
- = - ( +1 ) = -1 .

Wichtig dabei ist:

ist in beiden Fällen +1 , also positiv,
erst danach setzt man vor diese positive +1 ein Plus- bzw. Minuszeichen und
erhält damit nachträglich
- die positive Lösung +1 und auch
- die negative Lösung -1 .

Wichtig!!!: es wird also

weder eine negative Wurzel (aus einer positiven Zahl)
noch gar die Wurzel aus einer negativen Zahl gezogen.

Oder anders gesagt:

= +1 ,
- = - 1, aber
ist nicht definiert

(da die Umkehrung des Quadrierens ist, es aber keine

[sei's positive, sei's negative]

Zahl gibt, deren Quadrat negativ ist, denn das Quadrat jeder

[sei's positiven, sei's negativen]

Zahl ist positiv:

(+1)² = (+1) (+1) = +1 ,
(-1)² = ( -1) (-1) = +1 ).

Insegesamt gilt also:

1 = x² |

+ = x oder - = x

+1 = x oder -1 = x .

Kehren wir damit zu den obigen Rechnungen 1. und 2.a.. zurück, in denen wir beides Mal beim Wurzelziehen eine Lösung übersehen bzw. verloren hatten. Verbessert sehen diese beiden Rechnungen nun so aus:

                  0 = x³ - x      | + x

          x = x³           | : x

       + 1 = x²           |

+ = x oder -   = x

       +1 = x oder        -1 = x .

... d.h. durch die Nachbesserung erhalten wir in Rechnung 1. immerhin schon zwei (von drei) Nullstellen, nämlich +1 (+1 | 0) und N₃ ( -1 | 0).
a. 0 = x³ - x 0 = (x² - 1 ) • x

0 = (x² - 1 ) oder 0 = x

+ 1 = x² oder 0 = x

+ = x oder - = x oder 0 = x

+1 = x oder -1 = x oder 0 = x

... d.h. durch die Nachbesserung erhalten wir in Rechnung 2.a. alle drei Nullstellen N₁ (0 | 0), N₂ (+1 | 0) und N₃ ( -1 | 0).

Damit stellt sich "nur" noch die Frage, weshalb wir in 1. noch immer eine Nullstelle, nämlich N₁ (0 | 0), übersehen haben.

Schauen wir uns daher die Rechnung 1. nochmals genauer an:

0 = x³ - x | + x (A)

x = x³ | : x (B)

+ 1 = x² | (C1)

+ = x oder - = x (C2)

+1 = x oder -1 = x . (C3)

Wenn wir mal davon ausgehen, dass wir die gesamte Wurzelrechnung (C1 - 3) jetzt richtig gemacht haben, so bleiben als Fehlerquellen nur die Umformungen von Zeile (A) nach (B) bzw. von (B) nach (C1).

Nun ist aber die Umformung von Zeile (A) nach (B) zweifelsohne richtig

(wir haben nur auf beide Seiten der "Waage" jeweils ein [dasselbe] x gelegt, so dass die "Waage" im Gleichgewicht bleibt).

Als Fehlerquelle bleibt also nur noch die Umformung von Zeile (B) nach (C1) übrig, wo wir beide Seiten der Gleichung durch x geteilt haben.

Um aber im Bild der Waage zu bleiben: wenn ich die Gewichte auf beiden Seiten durch dasselbe x teile, so muss doch die Waage genauso im Gleichgewicht bleiben, wie wenn ich auf beiden Seiten dasselbe Gewicht x drauflege

(wie bei der Umformung von (A) nach (B) addiere)!?

Die Gemeinheit ist hier, dass das Problem so unsichtbar ist: das "Dingens", durch das wir da teilen, nämlich x, sieht so solide aus - und ist doch tückisch:

x kann jede beliebige reelle Zahl sein, und immer funktioniert die Division dadurch auch hübsch, bleibt beim Übergang von (B) nach (C1) also alles korrekt -
bis auf eine einzige, in mehrerlei Hinsicht unsichbare Ausnahme, nämlich x = 0:

am x steht eben nicht dran: "ich kann auch Null sein";
wenn die Null "nichts" bedeutet, ist sie per se unsichtbar, und überhaupt scheint "nichts" wenig bemerkenswert, obwohl doch die Null eine ganz besondere Zahl ist: ;

die einzelne Null verschwindet doch regelrecht zwischen den unendlich vielen anderen möglichen Zahlen.

Nun weiß jedeR SchülerIn: "durch Null darf man nicht teilen". Aber was heißt schon

(darauf wird unten zurückzukommen sein)

"weiß"?: das ist wie mit dem "passiven" und "aktiven" Wortschatz:

"passiver Wortschatz": wenn man (der Lehrer) direkt nachfragt, können die SchülerInnen es runterspulen, aber
"aktiver [eingeschränkter] Wortschatz": wenn ihnen unvermutet eine Aufgabe begegnet, in der es vorkommt, teilen sie dann eben doch gerne mal durch Null.

Und das liegt wiederum daran, dass der Satz "durch Null darf man niemals teilen" meist eine unverstande, nur widerwillig gelernte Weisheit ist: "Wenn der Lehrer es sagt, wird's wohl stimmen" bzw. "Ihm [und den Zensuren] zuliebe wollen wir's mal glauben - oder ihm zumindest nicht widersprechen."

Aber kümmern wir uns gar nicht darum, dass man nicht durch Null teilen darf, sondern schauen wir uns nur nochmal die beiden Gleichungen (B) und (C1) an:

x = x³ | : x (B)

+ 1 = x² (C1)

x = 0 ist

tatsächlich noch eine Lösung von (B) , denn 0 = 0³,
aber keine Lösung mehr von (C1), denn + 1 ≠ 0² .

Also wurde tatsächlich beim Übergang von (B) zu (C1) die Nullstelle N₁ (0 | 0) verloren, und es stellt sich die Frage, wie wir das verhindern können.

Es geht wohl kein Weg darum herum, folgenden Merksatz einzupauken:

Wenn man durch x

(oder in anderen Fällen einen "Term mit x")

dividieren will, mache man grundsätzlich eine kleine Pause und schaue sich immer genau an, was für x = 0 passiert

(bzw. wann der "Term mit x" Null wird).

In unserem vorliegenden Fall bedeutet das:

x = x³ | : x (B)

+ 1 = x² oder x = 0 (C1a)

Die Gesamtrechnung 1. sieht dann so aus:

0 = x³ - x | + x (A)

x = x³ | : x (B)

+ 1 = x² oder x = 0 | (C1a)

+ = x oder - = x oder x = 0 (C2a)

+1 = x oder -1 = x oder x = 0 (C3a),

und damit haben wir dann endlich auch in 1. alle drei Nullstellen N₁ (0 | 0), N₂ (+1 | 0) und N₃ ( -1 | 0) gefunden!

"[...] dass in der Mathematik die Zahl Null einen ganz speziellen Fall anzeigt und wir sie deswegen nicht mit einem x-beliebigen Messwert vergleichen können. Wenn wir bei der Vermessung von geometrischen Körpern immer wieder das Volumen Null feststellen, müsste man sich ja auch allmählich fragen, ob uns nicht jemand Flächen statt echte dreidimensionale Objeke untergejubelt hat."
(Quelle: )

Nun mag man sich denken: so ein gigantischer Aufwand (solch ein irrwitzig langer Text)

für die simple Aufgabe 0 = x³ - x ???
statt der fünfzeiligen Rechnung

0 = x³ - x | + x

x = x³ | : x

+ 1 = x² oder x = 0 |

+ = x oder - = x oder x = 0

+1 = x oder -1 = x oder x = 0 ???

Aber offensichtlich ist die Aufgabe "0 = x³ - x" eben nur scheinbar einfach, ja, ihre scheinbare Einfachheit ist ihre größte Gefahr.

"Scheinbar einfach" ist die Aufgabe auch, weil die SchülerInnen fallweise eine ganze Fülle von Vorkenntnissen mitbringen und ihre Anwendbarkeit erkennen müssen.

An einem einzigen Beispiel sei da nochmals der Vergleich mit dem "passiven/aktiven Wortschatz" zu bemüht:

es reicht nicht nur, dass die SchülerInnen

(wenn sie denn das Verfahren 2.b. wählen)

den "3. Binomi" in der allgemeinen Form (a+b)•(a-b) = a² - b² kennen,

sondern sie müssen ihn auch (ohne Anleitung) in x² - 1 wiedererkennen und dann anwenden können.

Und das ist gerade im scheinbar so einfachen Fall x² - 1 in Wirklichkeit so besonders schwierig:

sieht die 1 hinten nicht gerade quadratisch aus

(in x² - 1² könnte man viel leichter den "3. Binomi" erkennen),

2. ist die 1

(neben der Null)

die einzige Zahl, deren Quadrat identisch mit ihr selbst ist

(auch die 1 ist also eine ganz besondere Zahl: , und die 1 und die 0 zusammen sind sozusagen die Atome, aus denen sich alle anderen Zahlen [die Moleküle] zusammensetzen).

Z.B. würden die SchülerInnen sicherlich in x² - 16 viel besser den "3. Binomi", also

x² - 16 = x² - 4² = (x+4)•(x-4),

erkennen, da die 16 sehr viel "quadratischer" aussieht.

Hier also die nicht gerade kurze Liste der Vorwissens-Elemente, die die SchülerInnen sogar bei der noch relativ einfachen Aufgabe 0 = x³ - x fallweise kennen, selbstständig erkennen und anwenden können müssen

(und das Problem ist gerade das "fallweise"):

Nullstellen liegen vor, wenn y = 0,

Distributivgesetz,

a • b = 0

a = 0 oder b = 0,

Aufpassen bei der Division durch Null,

Fallunterscheidung beim Wurzelziehen: +1 = x oder -1 = x,

"3. Binomi".

Ich war oben mit dem Äquivalenzzeichenäußerst schludrig umgegangen, hatte es nämlich immer gesetzt. Dabei gilt es natürlich nur, wenn keine Lösung

dazukommt,
verloren geht,
sich verändert

(vgl. Variable (Heinzelmännchen) ).

Das pauschale Setzen von war aber natürlich pure Absicht:

die teilweise falschen Rechnungen 1. und 2.a. wirkten auf den ersten Blick derart suggestiv, dass ein allemal angebracht schien;
überhaupt ist das ja sowieso nur sinnvoll, wenn man permanent die Fälle mitbedenkt, in denen es nicht auftauchen darf, wenn man also Fehlermöglichkeiten erkennt;
die allermeisten SchülerInnen setzen sowieso immer (dem Lehrer zuliebe) ein , wenn der Lehrer überhaupt auf solche Wert legt;

Schauen wir uns an einem einzigen kurzen Auszug mal an, wann kein gesetzt werden darf, nämlich bei dem obigen Fehler

x = x³ | : x (B ; die Nullstelle N₁ (0 | 0) ist noch vorhanden)

+ 1 = x² (C1; die Nullstelle N₁ (0 | 0) ist abhanden gekommen)

Korrekt muss es hingegen heißen:

x = x³ | : x (B ; die Nullstelle N₁ (0 | 0) ist noch vorhanden)

+ 1 = x² oder x = 0 (C1; die Nullstelle N₁ (0 | 0) ist immer noch vorhanden)

In der korrekten Umformung **
folgern wir also

x = x³

+ 1 = x² oder x = 0

In der falschen Umformung *
folgern wir hingegen nur

x = x³

x = 0 .

Das ist vergleichbar mit

es ist Heiligabend

a) es ist Dezember

b) es ist der 24. Tag des Monats

Hier können wir aus den beiden Information a) und b) zusammen rückwärts folgern, dass es Heiligabend ist:

es ist Heiligabend

a) es ist Dezember

b) es ist der 24. Tag des Monats

es ist Heiligabend

b) es ist der 24. Tag des Monats

Hier können wir allein aus der Information b) nicht rückwärts folgern, dass es Heiligabend ist. Es könnte genauso gut der 24. Tag eines anderen Monats als des Dezembers, also z.B. der 24. Juli, vorliegen.

Entsprechend ist im Fall * nur

x = x³

x = 0

richtig.

Das bedeutet dabei, dass

zwar richtig gefolgert wurde, für x = 0 also tatsächlich eine Nullstelle der Ausgangsfunktion vorliegt

(immerhin haben wir also - was noch viel schlimmer wäre - keine vermeintliche Nullstelle hinzugemogelt),

das aber nur die halbe Wahrheit ist, weil zwei andere Nullstellen übersehen wurden bzw. unter den Tisch gefallen sind.

Mag sein, dass es mir nicht gelungen ist, den Sachverhalt so einfach zu erklären, wie es vielleicht tatsächlich möglich wäre (wie er ist?).

Ich befürchte aber eher, dass er so kompliziert ist und bleibt.