vgl. auch "Logarithmus (mathematische Größe): Der seit dem 17. Jh. bezeugte mathematische Fachausdruck ist eine Prägung des schottischen Mathematikers John Napier (1550-1617) aus griech. lógos »Wort; Rechnung; Verhältnis« und griech. arithmós »Zahl«. [...]" (Duden - Herkunftlexikon) "[...] meine 7Klässler (RS) fanden den Logarithmus die geilste Sache überhaupt, die sie je in Mathe erlebt haben. Ich stellte ihn als ein Geheimnis vor, das man den Realschülern vorenthalte. Seither unterrichte ich ihn sehr gerne - allerdings in unserer »Sonderschule«, auch für Hauptschüler, teilweise auch mit Rechenschieberübungen. [...]" (Peter Geist)

"Was vom Logarithmus übrigblieb" suggeriert, dass nur noch die letzten Leichenteile des Logarithmus zusammengefegt und dann vielleicht nostalgisch

(nach dem Motto "nur ein toter Logarithmus ist ein guter Logarithmus")

wie Fossilien/Reliquien verehrt werden können.

Dem sei doch gleich am wichtigsten Beispiel widersprochen - bzw. Totgesagte leben länger:

Wenn wir beispielsweise von "hundert" sprechen, so machen wir dafür ja keineswegs hundert Zeichen

(also z.B.  );

sondern

(um vorerst bei der Buchstabendarstellung bleiben)

nur 7, nämlich

h - u - n - d - e - r - t

1   2   3   4    5   6  7 .

Und in unserer Dezimal-Stellenwertschreibweise sind's sogar nur noch drei Zeichen:

1 - 0 - 0

1   2    3 .

Diese 3 ergibt sich aber als

3 = 2                  + 1 =

    = log₁₀(100)   + 1 .

Entsprechend ist

4 = 3                  + 1 =

    = log₁₀(1000) + 1   

die Anzahl der Ziffern von 1000 im Dezimal-Stellenwertsystem.

Bzw. mit der Schreibweise 1000 schreiben wir eben nicht 1000 Einzelzeichen auf

(also höchst umständlich

),

sondern glücklicherweise (!) nur 4 = log₁₀(1000) + 1  Ziffern.

Schauen wir uns das nun noch an einem Beispiel für eine "krummere" Zahl, nämlich 5497, an:

Am Ergebnis interessiert uns nur die Vor-Komma-Stelle, also

bzw. mathematisch gesprochen:

log₁₀(5497) =  3

(wobei "Gaußklammern" genannt werden und den ganzzahligen Anteil herausfiltern).

Nun gilt aber

                                 3 + 1 = 4,

und 4 ist ja in der Tat die Anzahl der Ziffern von 5497.

Allgemein gesagt:

die Anzahl der Ziffern einer (natürlichen) Zahl x ist gleich log10(x)  + 1.

log₁₀(x) ist also ein sehr gutes Maß für die Anzahl der Ziffern einer Zahl x;

bzw. log₁₀(x) gibt mit der Anzahl der Ziffern auch die ungefähre Größenordnung einer Zahl an, nämlich z.B. bei  5497, dass sie im Tausenderbereich liegt.

Und doch wird mir hier allzu leicht unterstellt, alle Menschen dächten "sowieso" logarithmisch: eben gerade die "logarithmische" Schreibweise des Dezimal-Stellenwertsystems scheint mir ja eine der Hauptursachen dafür zu sein, dass viele Menschen (und zwar insbesondere bei großen Zahlen) "zahlenblind" sind

(vgl. ):

die praktisch-kurze logarithmische Schreibweise wird eben mit enormer Abstraktion erkauft.

Ich bin derart alt, dass ich mich noch gut entsinnen kann, wozu Logarithmen einmal (vor allem) gut waren, nämlich zur erheblichen Vereinfachung alltäglicher (oder zumindest in der Schule anfallender) Rechnungen, die "in der guten alten Zeit", als es noch keine Taschenrechner gab, noch "mit der Hand" durchgeführt werden mussten.

Das Symbol dafür war die klassische

Logarithmentafel,

die damals noch jedeR SchülerIn andauernd mitschleppte.

All das ist aber nach Erfindung des Taschenrechners nur noch Erinnerung und darf nicht zur Nostalgie verkommen: wer wollte ernsthaft dahin zurück - und wer unter den Nostalgikern benutzt noch selbst eine Logarithmentafel?

Nun kann man natürlich den uralten Totschläger wieder hervorholen, was denn eigentlich sei, wenn mal alle Taschenrechner ausfielen. Ich glaube aber kaum, dass das überzeugend ist, denn zwar könnte - um effektheischend Horrorvisionen an die Wand zu malen - beispielsweise ein atomarer Blitz über einem Stromknotenpunkt tatsächlich alle elektrischen Geräte ausfallen lassen, aber dann hätten wir ganz andere Sorgen als läppische mangelnde Rechenfähigkeiten.

Vgl. beispielsweise 

"La Repubblica"

"Aber wenn es nicht das Werk von Bin Laden war, der den Strom abgestellt hat, wie es der Bürgermeister von New York unterstreicht, so scheinen die Stunden, die diese Metropolen und diese Millionen von Menschen durchlebt haben, doch so etwas wie eine Generalprobe des Schreckens zu sein, an deren Rand uns die Verletzlichkeit und Zerbrechlichkeit unserer Zeit geführt hat, nämlich zu einer absoluten Abhängigkeit von elektrischem Strom. Wenn jemand von weit her diese Stunden auf CNN verfolgt hat, dann wird er jetzt überzeugt sein, dass man keine Atombombe braucht, um eine Supermacht zu lähmen. Es genügt, dass man die Sicherung rausdreht."
(zitiert nach )

Dass Logarithmen handschriftliche Rechnungen enorm vereinfachen, ist heutzutage in Schulen also kaum mehr ein Argument.

Wenn überhaupt, so könnte die Behandlung dieses Themas "nur" noch einen historischen Grund haben:

1. die enormen Probleme früherer Generationen mit komplizierteren Rechnungen zu zeigen,
2. die Logarithmen als enorme Vereinfachung in früherer Zeit zu erfahren,
3. die immense Arbeit zu würdigen, die damals von Leuten geleistet wurde, die Logarithmentafeln überhaupt erst hergestellt (berechnet) haben

(und da könnte man ja vielleicht sogar ansatzweise zeigen, wie sie diese Logarithmentafeln aufgestellt haben, nämlich kaum durch probierende Annäherung, sondern durch systematische Reihenentwicklung, also durchaus interessante Mathematik; vgl. ).

Der "historische Grund" wäre also etwas, was in Schulen vielleicht allzu kurz kommt: Respekt vor den Schwierigkeiten und Lösungsversuchen der "Altvorderen".

Auch nur halbwegs überzeugend ist das Argument, dass Taschenrechner Rechnungen intern oftmals auch logarithmisch durchführen.

Vgl. etwa (und darauf wird unten zurückzukommen sein):

(zitiert nach )

Denn wen interessieren schon die "Innereien" von Taschenrechnern? Bzw. den meisten ist es doch herzhaft egal, wie ein Taschenrechner zu seinen Ergebnissen kommt, Hauptsache, sie sind richtig (und rasend schnell da).

Dass alle Technik heutzutage randvoll mit Mathematik ist, ist nur ein Scheinargument für die Mathematik: wenn man nämlich all die Mathematik in der Technik verstehen müsste, könnte ein Laie die meiste Technik gar nicht mehr nutzen.

(Und ich wette sogar, dass es nichtmal einen Nokia-Ingenieur gibt, der ein einziges Handy komplett versteht.)

Die Technik funktioniert also überhaupt nur deshalb so gut, weil man die Mathematik in ihr nicht verstehen muss.

Und dennoch ist es schade, dass viele Leute mit den Effekten zufrieden sind und nie wissen wollen, wie etwas funktioniert. Was vielleicht daran liegt, dass das "wie" (angeblich) sowieso zu schwierig ist. Dabei könnte man vielleicht doch relativ einfach grundsätzliche Funktionsweisen zeigen.

Das stärkste verbleibende Argument für die Behandlung von Logarithmen in den Schulen ist, dass allein mit ihnen Exponentialfunktionen

(wie sie beispielsweise auch in der Zinseszinsrechnung auftauchen)

gelöst werden können.

(Dabei seien hier nicht Sinn und Zweck der Behandlung von Exponentialfunktionen in der Schule diskutiert - womit man einwenden könnte, dass die Sinnfrage nur vom Logarithmus zu den Exponentialfunktionen umgelenkt worden, aber dadurch auch nicht befriedigend beantwortet sei.)

Wie man aber mittels der Logarithmen Exonentialfunktionen lösen kann, lässt sich in wenigen Sätzen erklären:

                    2^x   =         1000      |   log₂

     log₂ (2^x ) = log₂ (1000)
x • log₂ ( 2 ) = log₂ (1000)

x •      1        = log₂ (1000)

x                  = log₂ (1000)

Und da der Taschenrechner nunmal nicht zu jeder Basis (hier 2) eine eigene Taste haben kann, muss man nun nur noch log₂ (1000) in einen Zehnerlogarithmus umrechnen können:

log₂ (1000) =

Das nun aber kann der Taschenrechner tatsächlich berechnen - und gibt als Lösung x ≈ 9,9657 an.

Dieses stumpfe Rechenverfahren lässt sich in wenigen Minuten erklären, und um es anzuwenden, muss man weder die benutzten beiden Logarithmengesetze noch überhaupt verstanden haben, was der Logarithmus eigentlich ist.

Natürlich ist einE richtigeR MathematikerIn (bzw. einE richtigeR MathelehrerIn) nicht mit solch stumpfen, d.h. zwar wirksamen, aber doch unverstandenen Rechenverfahren zufrieden, zumal sie ja allzu schnell wieder vergessen werden.

Halten wir aber immerhin schon mal fest:

Und man kann sich sogar noch das zweite Gesetz sparen, wenn man

(obwohl doch in der ursprünglichen Exponentialgleichung 1000 = 2^x nicht die 10, sondern die 2 die Basis ist)

 von Anfang an mit dem Zehnerlogarithmus rechnet:

log (2^x ) = x • log ( 2 )  

Das ganze Problem steckt - wie so oft in der Mathematik - in der Wortkombination "man braucht":

• wer ist "man",
• und was braucht dieser "man" denn wozu?

Der durchschnittliche Bürger braucht Logarithmen (wie auch alle andere Schulmathematik) nie, wenn er nicht später Naturwissenschaften oder Technik studiert.

SchülerInnen brauchen Logarithmen tatsächlich nur, um Exponentialgleichungen lösen zu können

(nochmals: deren innerschulischer Sinn hier nicht diskutiert werden soll).

Die uralte Frage ist halt, ob die Schulmathematik

(abgesehen vielleicht von der Vermittlung einiger weniger Rechenfertigkeiten, zu denen wohl kaum das Lösen exponentieller Gleichungen mittels Logarithmus gehört)

überhaupt für eine direkte Verwertbarkeit da ist - oder ob es um viel allgemeinere   geht. 

Im Hinblick auf den Logarithmus wäre also zu fragen, ob bzw. welche typischen mathematischen Denkweisen sich bei ihm zeigen, oder gar, ob sie sich an ihm besonders gut zeigen.

(Und überhaupt sollte man sich bei einem spezifischen mathematischen Stoff viel mehr als üblich fragen, zur Vermittlung welcher mathematischen Denkweisen bzw. "Ideen" er [nicht] besonders geeignet ist, statt nur nach seinem "Selbstwert" zu fragen. Letzterer ist nämlich oftmals aus reiner Gewohnheit nur allzu suggestiv - und in Wirklichkeit gar nicht gegeben.)

Denkbar wäre es ja durchaus, dass spezifische mathematische Denkweisen sich auch (oder sogar besser) an anderen mathematischen Gegenständen zeigen, so dass "es nicht unbedingt der Logarithmus sein muss".

Dazu ein Beispiel:

• Sowohl die Wurzel als auch der Logarithmus sind schöne Beispiele für die typische mathematische Denkweise :
  • die Wurzel aus 7 ist diejenige Zahl, die mit sich selbst malgenommen (quadriert) 7 ergibt: • = ()² = 7
  • der Logarithmus von 7 (x = log₂7) zur Basis 2 ist diejenige Zahl, mit der ich 2 potenzieren muss, um 7 zu erhalten: 2^x = 7.

(... und in beiden Fällen sind die Mathematiker an diesen Um-die-Ecke-Definitionen viel interessierter als an den [oftmals zudem irrationalen] Dezimalwerten.) 

• die Um-die-Ecke-Definitionen zeigen schon eine weitere Gemeinsamkeit:
  • die Wurzelfunktion ist Umkehrfunktion der quadratischen Funktion,
  • die Logarithmusfunktion ist Umkehrfunktion einer Exponentialfunktion

(in beiden Fällen mit der Folge, dass sich die Graphen der Wurzel- bzw. Logarithmusfunktion aus den Originalfunktionsgraphen durch Spiegelung an der Winkelhalbierenden des ersten Quadranten ergeben). 

Ich meine aber, dass es reicht, die gezeigte Gemeinsamkeit an einem Beispiel zu zeigen - und da würde ich allemal die Behandlung der Wurzel vorziehen, zumal die so schön mit der Erarbeitung der Irrationalität (einer anderen wichtigen mathematischen Idee) verbunden ist, die man bei Wurzeln relativ einfach zeigen kann

(vgl. ),

bei Logarithmen aber wohl kaum.

Nein, der eigentliche "Gag" bzw. die eigentliche

(und im Vergleich mit allem vorherigen Unterrichtsstoff neue, wenn auch teilweise auf diesem aufbauende)

mathematische Idee hinter dem Logarithmus ist eine ganz andere, die sich allerdings schon oben bei der

(dort allerdings noch als Unterrichtsthema verworfenen)

Vereinfachung von Rechnungen und bei der Funktionsweise von Taschenrechnern angedeutet hat:

... und Computer noch weniger

Früher waren die großen Mathematiker (notgedrungen, da nicht mit einem Taschenrechner ausgerüstet) oftmals auch große Rechenkünstler (vgl. etwa Gauß und Euler). Heutzutage ist es aber eine ebenso falsche wie gleichzeitig doch unausrottbare Einschätzung, Mathematiker könnten gut rechnen und Mathematik sei überhaupt die Kunst des Rechnens. Nein, Mathematiker rechnen fast nie, sondern kümmern sie vielmehr um mathematische "Strukturen", und wenn dann doch mal Rechnen nötig sein sollte, greifen sie eben auch zum Taschenrechner.

Der Laie mag also staunen, dass (auch) MathematikerInnen ihre lieben Schwierigkeiten mit den "gehobeneren" und dennoch "Grund"-Rechenarten Multiplikation, Division und Potenzrechnung haben.

Und mal Hand aufs Herz: wer kann im Zeitalter des Taschenrechners oder viele Jahre nach der Schulzeit noch korrekt eine (hand-)schriftliche

• Multiplikation
• oder gar Division  

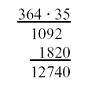
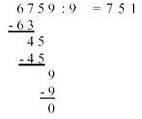
(und dann auch noch mit Rest und Periode)

durchführen?

Wenn man aber genauer hinschaut, so fällt an der schriftlichen Multiplikation und Division etwas Bemerkenswertes auf:

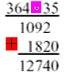• in wird die Multiplikation auf eine (einfachere) Addition zurückgeführt,
• in wird die Division auf (einfachere) Subtraktionen zurückgeführt.

Und das hat seine guten Gründe, wie hier nur anhand der Multiplikation/Potenzrechnung gezeigt werden soll: 

• die Potenzrechnung ist eine verkürzte Multiplikation:

3⁴ = 3 • 3 • 3 • 3

• und die Multiplikation ist wiederum eine verkürzte Addition ist:

         3 • 5 = 3 + 3 + 3 + 3 + 3 ,

• also die Potenzrechnung letztlich eine extrem verkürzte Addition:

3⁴ = 3 • 3 • 3 • 3 =     (3 + 3 + 3) + (3 + 3 + 3) + (3 + 3 + 3) +

                              + (3 + 3 + 3) + (3 + 3 + 3)  + (3 + 3 + 3) +

                              + (3 + 3 + 3) + (3 + 3 + 3)  + (3 + 3 + 3)

Typisch für das "strukturelle" Denken ist dabei, dass uns die rechnerischen Endergebnisse, also

• 3⁴ = 81,
• 3 • 5 = 15

gar nicht interessieren, ja dass sie uns sogar von der Erkenntnis der "Struktur" ablenken würden.

Schnell werden die Vor- und Nachteile der verschiedenen Schreibweisen klar:

• Vorteile:
  • mit der Potenzschreibweise  3⁴ und der Multiplikationsschreibweise 3 • 5 lassen sich mittels weniger Zahlen (nur einer 3 sowie einer 4 bzw. einer 5) große Zahlen sehr kurz darstellen

(besonders deutlich wird das etwa an 10²⁰ = 100000000000000000000);

• die Potenz- und die Multiplikationsschreibweise verhindern Flüchtigkeitsfehler (eine Zahl/Ziffer zu wenig oder zu viel); so ist
  • 3 • 5 viel weniger fehleranfällig als 3 + 3 + 3 + 3 + 3,
  • 3⁴viel weniger fehleranfällig als     (3 + 3 + 3) + (3 + 3 + 3) + (3 + 3 + 3) +

•                                                                     + (3 + 3 + 3) + (3 + 3 + 3)  + (3 + 3 + 3) +

                                                                      + (3 + 3 + 3) + (3 + 3 + 3)  + (3 + 3 + 3)

  • und 10²⁰ viel weniger fehleranfällig als 100000000000000000000.
• Nachteile:
• das Rechnen mit Potenzen und Multiplikationen ist erheblich schwieriger als die Addition,
• unter 3⁴ und mehr noch 10²⁰  kann man sich schwerlich was vorstellen, da 3⁴ und 10²⁰ nur Rechenanweisungen sind

("nimm die Drei vier mal mit sich selbst bzw. die zehn zwanzig mal mit sich selbst mal") ,

aber das Ergebnis (81 bzw. 100000000000000000000) verschweigen; und spätestens das Ergebnis 100000000000000000000 ist ebenfalls schier unvorstellbar.

('tschuldigung, aber in welchem Matheunterricht wird sowas Grundlegendes wie gleichzeitig doch in höhere Mathematik Führendes denn mal explizit erarbeitet?)

Eine wichtige Folge des Zusammenhangs Potenzen → Multiplikation (Division) → Addition (Subtraktion) sind die (hier nicht bewiesenen) Potenzgesetze:

1. a^m • aⁿ = a^m+n, wo eine              Multiplikation auf eine Addition zurückgeführt wird,
2. a^m : aⁿ = a^m-n, wo eine               Division         auf eine Subtraktion zurückgeführt wird,
3. (a^m)ⁿ = a^m•n  , wo eine doppelte Potenz          auf eine Multiplikation zurückgeführt wird.

Wirklich hilfreich wird das aber erst mit den Logarithmengesetzen, die ihrerseits auf die Potenzgesetze zurückgeführt werden können

(man könnte also sagen, dass die Logarithmengesetze die logische Krönung aller vorherigen jahrelangen Beschäftigung mit Rechenarten sind):

1. log (a • b) =      log a + log b, wo eine Multiplikation auf eine Addition        zurückgeführt wird,
2. log (a : b) =      log a  - log b, wo eine Division         auf eine Subtraktion   zurückgeführt wird,
3. log (aⁿ   ) = n • log a            , wo eine Potenz          auf eine Multiplikation zurückgeführt wird,

Mit dem 1. und 2. Logarithmengesetz sind damit Gesetze erwähnt, die oben noch als

(fürs tägliche Rechnen im Zeitalter des Taschenrechners)

überflüssig abgetan worden waren, während das 3. Logarithmengesetz oben ja schon als nötig für das Lösen von Exponentialgleichungen dargestellt worden war.

Nun sind die Logarithmengesetze mit der Rückführung Potenzen → Multiplikation (Division) → Addition (Subtraktion) zwar theoretisch interessant, aber was hat(te) man davon

("hatTE" in der Zeit vor Erfindung von Taschenrechnern)?

Mit den Logarithmengesetzen ist es nun eben möglich, die - wie oben gezeigt - schwierigen Potenzrechnungen sowie Multiplikationen (Divisionen) auf einfache Additionen (Subtraktionen) zurückzuführen, und das funktioniert - an zwei Beispielen gezeigt - folgenermaßen:

1. angenommen, die beiden Zahlen 1734 und 849 sollen miteinander multipliziert werden. Dazu entnimmt man einer Logarithmentafel die Logarithmen der beiden Zahlen

(wobei wir hier der Einfachheit halber den Zehnerlogarithmus, also log₁₀ = log, benutzen),

         nämlich,

• log (1734) ≈ 3,2390,
• log ( 849)  ≈ 2,9289.

Nun werden diese beiden Zahlen ganz simpel (schriftlich!) addiert:

                            3,2390
                         + 2,9289
                            6,1679

Und zu diesem Ergebnis 6,1679 schlägt man nun in der Logarithmentafel wieder die ursprüngliche Zahl (den sogenannten Numerus) nach und erhält  1.472.166.

Oder kurz gesagt: 1734 • 849 = 1.472.166

2. angenommen, es soll 17^1,5 berechnet werden.

Dazu schlägt man in der Logarithmentafel nach:

• log (17) ≈  1,2304.

Diese Zahl 1,2304 multiplizieren wir (was schon ein wenig einfacher ist) mit 0,5, rechnen also

• 1,2304 • 1,5.

Auch diese Multiplikation ist uns noch zu schwierig, und deshalb reduzieren wir sie (wie in 1. gezeigt) in einem zweiten Schritt auf eine Addition, indem wir wieder die Logarithmen beider Zahlen nachschlagen:

• log (1,2304) ≈  0,09004,
• log (     1,5 ) ≈  0,17609

Diese beiden werden nun addiert:

                             0,09004
                         + 0,17609
                            0,26613

Wie gehabt, suchen wir zu diesem Ergebnis 0,26613 in der Logarithmentafel den Numerus und erhalten 1,84556.

Und zu dieser Zahl 1.84556 nochmals der Numerus ist  70,0927.

Oder kurz gesagt: 17^1,5  ≈ 70,0927.

Man störe sich nicht an dem scheußlichen (beim Exponenten 1,5 aber erwartbaren) Ergebnis 70,0927. Wichtig ist hier vor allem, dass wir

• nicht nur die Potenzrechnung auf dem Umweg über eine schon einfachere Multiplikation in eine vollends einfache Addition überführen,
• sondern sogar die ansonsten aussichtslos komplizierte (und unanschauliche!) Rechnung mit einem gebrochenen Exponenten (hier 1,5) durchführen konnten

(und somit auch - das sei nur kurz ohne Erklärung ergänzt - sogar das Wurzelziehen auf eine Addition vereinfachen können).

Wie typisch für die Mathematik, erkauft man sich allerdings die Vereinfachung (Reduktion auf eine Addition) mit einer Erschwerung (Einführung des Logarithmus sowie Anwendung von Logarithmengesetzen).

Allerdings war dieser Umweg vor Einführung der Taschenrechner unumgänglich bzw. brauchte man bis dahin komplizierte Mathematik, um relativ einfache Aufgaben (schnelles Potenzieren und Multiplizieren [Dividieren]) zu lösen.

Und all das hilft wenig, wenn man keine Logarithmentafeln hat. Diese aber wurden in immenser Arbeit von einigen Mathematikern erstellt - um damit für Jahrhunderte (bis zur Erfindung des Taschenrechners) allen Anwendern das Leben viel einfacher zu machen.

Dank gebührt da insbesondere

John Napier

Ansonsten gibt es wichtige Anwendungen der Logarithmen, von denen hier nur drei kurz erwähnt seien:

1.  "Der pH-Wert ist ein Maß für die Stärke der sauren bzw. basischen Wirkung einer wässrigen Lösung. Als logarithmische Größe ist er durch den mit -1 multiplizierten dekadischen Logarithmus (= "Zehnerlogarithmus") der Oxoniumionenkonzentration (genauer: der Oxoniumionenaktivität) definiert."
   (Quelle: )

... wobei "Oxoniumionenkonzentration"  und  "Oxoniumionenaktivität" für mich erstmal böhmische Dörfer sind; dafür, dass der ph-Wert überhaupt logarithmisch berechnet wird, gibt es aber immerhin folgende ansatzweise Erklärung:

"Um nicht immer mit Potenzzahlen rechnen zu müssen, werden logarithmische Grössen eingeführt."
(Quelle: )

Was aber wirklich dahinter steckt, wird sehr schön an einer typisch harmlos-abstrakt daherkommenden Standardaufgabe aus einem alten Schulbuch klar:

"Berechne log (10³⁶⁵)!"

Das Schöne (!) daran ist, dass die notwendige Ersteingabe 10³⁶⁵ bei einem handelsüblichen Taschenrechner gar nicht möglich ist

(10³⁶⁵ ist viel zu groß, als dass der Taschenrechner die Eingabe akzeptieren geschweige denn damit rechnen könnte)

- und somit auch nicht die Zweiteingabe "log".

Man kommt also - glücklicherweise! - um die Kenntnis immerhin eines Logarithmengesetzes gar nicht herum:

log (10³⁶⁵) = 365 • log (10) = 365 • 1 = 365

Das entsprechende Logarithmengesetz und überhaupt der Logarithmus machen es also erst möglich, dennoch mit gigantischen Zahlen rechnen zu können.

(Es gibt also viel zu viele scheinbar harmlose Matheaufgaben, deren Dramatik unbedingt ergänzt werden muss.)

• Eine im Matheunterricht oftmals viel zu selten behandelte Besonderheit des Logarithmus ist folgende:

  • log ₂ 2   = 1, denn 2¹ = 2            (A)
  • log ₂ 4   = 2, denn 2² = 4            (B)
  • log ₂ 8   = 3, denn 2³ = 8            (C)
  • log ₂ 16 = 4, denn 2⁴= 16           (D)
  • ...

  Während also die rote Zahl sich jeweils verdoppelt, steigt der Logarithmus jeweils nur um 1, weshalb der Funktionsgraph so aussieht:

  

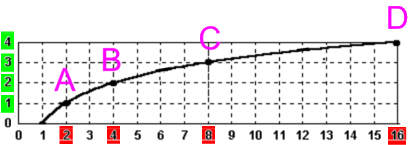
  Der Graph steigt also immer langsamer.

  Aber was bedeutet das?

  *

  

  Und da heißt es dann:

  "[...]

  Was aber steckt hinter dem uns offensichtlich innewohnenden logarithmischen Denken? Dehaene und seine Kollegen verweisen auf das sogenannte Weber-Fechner-Gesetz. Schon vor über 170 Jahren hatte der Physiologe Ernst Heinrich Weber festgestellt, dass die Stärke von Sinneseindrücken sich logarithmisch zur Intensität des physikalischen Reizes verhält. Der Logarithmus ist uns Menschen offenbar regelrecht einprogrammiert.

  Aber auch die Evolution könnte nachgeholfen haben: Die logarithmische Skala ist einfach kompakter als eine lineare, erklären die Forscher. Man könne damit leicht mehrere Größenordnungen auf einmal überblicken - und dies relativ präzise.

  Dieser Gedanke leuchtet ein: Die Unterscheidung, ob zwei oder drei Mitglieder eines feindlichen Stammes sich nähern, ist wichtiger als die Frage, ob eine größere Angreifergruppe nun aus 25 oder 30 Personen besteht. Je größer die Zahlen sind, umso mehr kommt das Prinzip Pi mal Daumen zum Tragen - auch aus praktischen Gründen.

  [...]"

  Der Logarithmus ist also mit einer Gleitsicht-Lesebrille vergleichbar, die große (weit entfernte) Dinge unverändert lässt, aber kleine (nahe) Dinge vergrößert:

  

  (... wobei das Bild der Gleitsichtbrille allerdings hinkt, da weit Entferntes ja sowieso kleiner wirkt.)

  Was da passiert, sei nochmals an zwei Beispielen gezeigt:

  • der Logarithmus zeigt kleine Werte ziemlich genau: es ist beispielsweise durchaus von Bedeutung, ob jemand 500 Euro oder 510 Euro im Monat verdient: die 10 Euro extra könnten gerade das Mittagessen sein, das einen Hartz-IV-Empfänger vorm Verhungern rettet;

  • der Logarithmus zeigt große Werte sehr ungenau: es ist beispielsweise nebensächlich, ob Bill Gates ein Vermögen von 50 Milliarden Dollar hat oder 10 Dollar mehr, die für ihn doch nur "peanuts" sind.

3. Vgl. .

Vgl. auch .