"Mindest[= ]löhne sind imaler Unsinn." (FDP-Generalsekretär Dirk Niebel am 16.10.08; wobei die Äußerung natürlich selbst maximaler Unsinn ist) "[...] Das Gitter aus sechseckigen Kammern ermöglicht es dem Bienenvolk, die größtmögliche [=  ] Menge Honig im größtmöglichen [=  ] Raum unterzubringen und gleichzeitig eine möglichst geringe [=  ] Menge Wachs für den Bau der Wände zu verwenden. Während die Bienen seit langem wissen, dass das Hexagon [=regelmäßige Sechseck] die effizienteste Form für einen Honigspeicher ist, ist es den Mathematikern erst vor Kurzem gelungen, das Geheimnis der Bienenwabe zu lösen [...]" (zitiert nach ) "[...] können Bäume ewig zunehmen? Theoretisch ja. Aber sie wachsen nicht blindlings drauflos. Das Wachstum in die Breite steht mathematisch genau im richtigen Verhältnis zur Höhe und zum Gewicht des Baumes. Und ein Baum passt auch seine äste auf subtile Weise den angreifenden Belastungen an. Wissenschaftlern zufolge haben Bäume im Lauf der Evolution gelernt, Verluste einzukalkulieren. Gelegentliche Schäden kosten weniger als ständiger Aufbau. So sind Bäume zu Ingenieuren und Konstrukteuren geworden, die man sich auch in unserem Wirtschaftsleben wünschte: Sie erreichen mit minimalem Materialaufwand eine maximale Stabilität.[...] (zitiert nach ) "[...] Gebilde, die fraktal angelegt sind, machen das schier Unmögliche möglich: die größtmögliche flächenmäßige Erschließung mit dem geringstmöglichen Aufwand. Ein fraktales Versorgungsgeflecht löst das Problem, jeden Punkt des Körpervolumens mit Nährstoffen zu versorgen, dabei nicht das gesamte Volumen einzunehmen und die Nährstoffe innerhalb einer bestimmten Zelt umzuwälzen. So kann zum Beispiel die menschliche Lunge auf einem relativ kleinen Volumen immerhin eine Fläche von 100 Quadratmetern entfalten. Der amerikanische Physiker Geoffrey West konnte nachweisen, dass das fraktale Modell nicht nur auf das Atmungssystem von Wirbeltieren oder das Tracheensystem von Insekten anwendbar ist, sondern genauso bei Gefäßen von Pflanzen funktioniert: »All diesen Systemen liegt dieselbe Logik zugrunde. Weil die Ressourcen über ein Transportsystem verteilt werden, das eine bestimmte Fläche einnimmt – Lungenoberfläche, Blattoberfläche, Wurzeloberfläche –, hat die Evolution das Ausmaß dieser Fläche maximiert. Und gleichzeitig wurde dafür gesorgt, dass die internen Transportwege so kurz wie möglich sind. [...]« [...]" (zitiert nach ) : (, 9.7.09) Was bedeutet "[...] die Abwärtsdynamik merklich abgeschwächt"?

Im Grunde ist mit schon alles gesagt:

Ziel ist immer (auf dem lästigen, aber unvermeidbaren Umweg über die "Randbedingung") eine "Zielfunktion", von der entweder das mum oder das imum zu bestimmen ist.

Dabei sei vorausgesetzt, dass die rechnerische bestimmung einer rein mathematischen Zielfunktion bereits bekannt ist und beherrscht wird. Hier geht es (unter anderem) vor allem darum, diese Zielfunktion überhaupt erst zu finden.

---

Zwar sind die folgenden Aufgaben alle aus demselben, nämlich geometrischen Anwendungsbereich, aber sie unterscheiden sich dennoch nach typischen Problemen:

1. Aufgabe: maximaler Schachtelinhalt

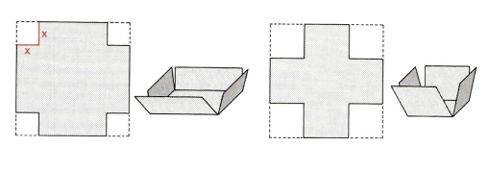
Aus einem DIN-A4-Blatt soll eine (kubische) Schachtel gebildet werden, die maximales Volumen hat.

Der Einfachheit halber

• seien dabei doch keine Klebefalze betrachtet,
• soll die Schachtel keinen Deckel haben.

Zwei Vorüberlegungen:

• Trotz der Vereinfachung liegt hier

(wie auch das ähnliche Bienenwabenbeispiel oben zeigt)

ein echtes Anwendungsproblem vor, denn in der Verpackungswirtschaft spielen selbstverständlich ressourcen- und umweltfreundliche Überlegungen wie "maximales Volumen / kleinstmöglicher Materialverbrauch" eine wichtige, wenn auch nicht immer die entscheidende Rolle.

(Nebenbei:

• Sind eigentlich die beiden Forderungen "maximales Volumen / kleinstmöglicher Materialverbrauch" miteinander vereinbar?
• Andere als ressourcen- und umweltfreundliche Überlegungen sind beispielsweise Praktikabilität [in der Herstellung und im Gebrauch], Ästhetik ... - woraus folgt, dass die mathematisch beste Entscheidung noch lange nicht die ansonsten günstigste ist, was am Ende jeder Anwendungsaufgabe zu diskutieren ist!)

Schon hier zeigt sich, dass sehr viel mehr zu tun ist als im üblichen Unterricht, in dem die Aufgaben nur unhinterfragt nach dem Prinzip "friss oder stirb" wegzurechnen sind:

zumindest beim Einstieg in "angewandte" Minimaxaufgaben sollte man mit den SchülerInneN nämlich diskutieren, ob tatsächlich Anwendungsnähe (nicht unbedingt gleich "Lebensnähe") vorliegt: ob sich das Problem also in irgendeinem Anwendungsbereich überhaupt so oder ähnlich stellt.

Oder sind die vermeintlichen Anwendungsaufgaben nur ?

• Im Grunde ist die Aufgabenstellung allzu suggestiv, denn sie setzt voraus, dass nicht alle möglichen Schachteln dasselbe Volumen haben, sondern eine (einzige) Schachtel das maximale Volumen hat.

Eine nicht suggestive Aufgabe wäre hingegen "Bilde aus dem Blatt eine (x-beliebige) Schachtel". Damit ergäben sich schon einige Überlegungen zur grundsätzlichen Konstruktion (s.u.) solcher Schachteln, und wenn man erstmal verschiedene Schachteln gebastelt hätte, wäre vielleicht auch die Frage nach dem maximalen Volumen naheliegend.

Immerhin ist die Ausgangsaufgabe mit der Frage nach dem maximalen Volumen aber insofern nicht suggestiv, als unklar bleibt, welche der vielen möglichen Schachteln maximales Volumen hat.

Und damit könnte man es eben doch als Herausforderung verstehen, die SchülerInnen echte Schachteln basteln zu lassen und auszuprobieren, welche der von den verschiedenen SchülerInnen angefertigten verschiedenen Schachteln maximales Volumen hat

(wobei dann auch nochmals deutlich wird, dass nicht alle möglichen Schachteln dasselbe Volumen haben).

Genau das kommt mir im üblichen (Anfangs-)Unterricht aber eben auch zu kurz: dass die Probleme (soweit möglich) praktisch und nicht nur theoretisch angegangen werden.

Natürlich "frässe" das Zeit, die beim zunehmenden Stoffdruck und höchst einseitigen Prüfungsaufgaben vielleicht beim besten Sinne nicht mehr abzuzwacken ist.

Ich bin dennoch der festen Überzeugung, dass es sinnvoll genutzte Zeit wäre: das Grundproblem vieler SchülerInnen bei Anwendungsaufgaben liegt doch nicht in der eigentlichen Mathematik (dem Rechnen), sondern darin, dass sie sich das Anwendungsproblem nicht vorstellen können. Wie soll aber jemand, der keinerlei Vorstellung hat, überhaupt

• zu einer Mathematisierung (Zielfunktion, Randbedingung) kommen
• und danach innermathematisch rechnen können?

Man kann es sich natürlich sehr einfach machen und

(weil die SchülerInnen es ja [angeblich] "sowieso" nicht können oder weil für ihre eigene Problemdurchdringung zu viel Zeit verginge)

die Anschauung sowie zusätzliche wichtige Lösungsideen vorgibt - wie es etwa in einem Schulbuch

(für den Sonderfall eines quadratischen Ausgangsblattes)

geschieht:

Daran habe ich doch allerlei auszusetzen:

1. schon allein, dass das ursprünglich dreidimensionale Problem notgedrungen auf zweidimensionale Projektionen reduziert wird, wobei ich mich frage, ob dadurch alles schwieriger oder einfacher wird;
2. , weil schon allein die Vorgabe des quadratischen Papiers auch quadratische Ausschnitte an den Ecken suggeriert; und dass dadurch überhaupt andere (nichtquadratische, d.h. hier rechteckige) Papierformen und damit "allgemeinere" Zusammenhänge von Anfang an ausgeschlossen sind;
3. , dass eben - wie schon erwähnt - die zentrale Idee vorweg schnöde verraten wird: dass an allen Papierecken Quadrate derselben Seitenlänge x ausgeschnitten werden müssen

(da mag man einwenden, dass das doch allzu selbstverständlich sei und deshalb nur ein offenes "Geheimnis" verraten werde; wir werden aber unten sehen, dass es für viele SchülerInnen keineswegs selbstverständlich ist).

Ich hab´s also in einem Kurs mal wirklich machen (!) lassen - und das verlief

(beim standardmäßig zur Verfügung stehenden nichtquadratischen DIN-A4-Blatt)

so:

1. zeichnete eine Schülerin folgende Planskizze an die Tafel:

2. Die Planskizze war derart suggestiv, dass ausnahmslos alle SchülerInnen beim dann folgenden Basteln eine horizontale und vertikale (gleichmäßige) Dreiteilung des Blattes versuchten

(... wobei sich ganz nebenbei herausstellte, dass eine Dreiteilung gar nicht so einfach ist - und welcher Trick da hilft).

Damit ergaben sich dann folgende Schachteln:

Wohlgemerkt: bei der Vorgabe eines DIN-A4-Blattes erhalten nach diesem System alle SchülerInnen dieselbe Schachtel (Singular!), womit die Frage nach der mit dem größten Volumen hinfällig ist.

(Nebenbei: wenn überhaupt, so wäre die Einheitsschachtel nur zufällig die größte.)

Kommt hinzu, dass die gelben Flächen überstehen, was doch immerhin nahelegt, dass die unnütze Materialverschwendung sind und es somit eine größere Schachtel gibt.

Schneidet man nun aber die gelben Flächen ab und klappt die Schachtel wieder auf, so sieht man (jetzt erst!), dass an allen Ecken gleichgroße Quadrate abzuschneiden sind, womit sich vielleicht auch erneut die Frage ergibt, wie groß denn diese Quadrate sein müssen, um maximales Volumen zu erreichen.

Zumindest haben "meine" SchülerInnen dann sofort mit verschieden großen Quadraten experimentiert, oder genauer: viele EinzelSchülerInnen hatten ziemlich genaue (unterschiedliche!) Vorstellungen davon, wie groß die Quadrate sein müssten, damit eine Schachtel mit maximalem Volumen entstünde. Und trotz teilweise extrem unterschiedlicher Bastelergebnisse der EinzelSchülerInnen waren einige doch fest überzeugt, die einzig wahre Lösung zu haben, was natürlich die Frage aufwirft, wer denn nun Recht hat bzw. ob unterschiedliche (oder gar alle) Schachteln dasselbe (maximale) Volumen haben können.

Zwecks Entscheidung, welche der Schüler-Schachteln denn nun die größte Volumen

(wenn auch nicht unbedingt das größtmögliche)

hat, könnte man natürlich die verschiedenen Schachtelvolumina ausrechnen

(änge mal Breite mal Höhe),

was aber nur schnöde Zahlen, also keine "handgreiflich"-dreidimensionalen Volumina und somit auch keine eindrückliche Anschauung ergäbe.

Wir haben deshalb in dem entsprechenden Kurs die Schachteln foliiert, geknickt, an den offenen Kanten mit Tesafilm zugeklebt, mit Wasser gefüllt und dann das Wasser in jeweils einer Schachtel in eine andere umgeschüttet, wobei meistens Wasser überfloss oder zu wenig Wasser vorhanden war, sich also zeigte, dass die Schachteln unterschiedlich groß waren.

So ergab sich dann tatsächlich eine größte Schachtel, wobei allerdings allen SchülerInnen klar war, dass das nicht notwendig die größtmögliche Schachtel sein musste.

Immerhin hatte man mit der größten Schachtel aber eine ungefähre Vorstellung von der größtmöglichen Schachtel und konnte somit Überlegungen anstellen, warum die größte Schachtel ein so besonders großes Volumen und war Schachteln sehr flache oder sehr hohe Schachteln sehr wenig Volumen haben.

... womit schon eine weitere meiner Forderung naheliegt:

Wenn möglich, sollten vor aller Rechnung Vermutungen angestellt werden, wie das Ergebnis rein anschaulich aussehen könnte. Und auf solche Vermutungen ist natürlich nach allen Rechnungen zurück zu kommen: hat man gut vermutet - und weshalb? hat man schlecht vermutet - und weshalb? (Z.B. auch [was eine ungeheuer wichtige Erfahrung ist], weil einen der "gesunde Menschenverstand" gründlich irreführen kann. Kann man dann dem "gesunden Menschenverstand" nachträglich nachhelfen, indem man etwa zeigt, die das mathematische Ergebnis zustande gekommen ist, oder erweist sich, dass die mathematische Abstraktion letztlich uneinholbar, aber eben auch unvermeidbar ist?)

Nachdem nun also klar geworden ist, dass an allen Ecken gleichgroße Quadrate ausgeschnitten werden müssen, ergibt sich folgendes Bild:

Unklar dabei ist allerdings noch, wie groß die Quadrate sein müssen, damit ein maximales Schachtelvolumen entsteht.

Hier sind nun (noch sehr intuitive) Überlegungen zu den Randextrema sinnvoll:

1. Welches ist das größtmögliche Quadrat, das man ausschneiden kann - und wie sieht die dann entstehende Schachtel aus?
2. Welches ist das kleinstmögliche Quadrat, das man ausschneiden kann - und wie sieht die dann entstehende Schachtel aus ?

Zum einfacheren Fall A.:

Das größtmögliche ausschneidbare Quadrat hat somit als Seitenlänge die halbe Papierbreite: x = .

Der Laie würde nun sagen, dass bei dieser Quadratseitenlänge überhaupt keine Schachtel entsteht, während der Mathematiker einfach dreist sagt: doch, es entsteht sehr wohl eine Schachtel, die allerdings die Boden-/Schachtelbreite 0 hat, weshalb

(wegen Volumen = Länge mal Breite mal Höhe)

auch ihr Volumen 0 ist.

Zu B.:

Hier tritt ein ähnliches Problem auf: der Laie wird noch einsehen, dass man beliebig kleine Quadrate ausschneiden kann und damit extrem flache Schachteln erhält. Aber es wird ihm schwer fallen, auch noch den Extremfall zu akzeptieren: wir schneiden gar nichts aus, also (paradoxerweise) Quadrate der Seitenlänge x = 0, und auch dann ergibt sich

(wieder wegen Volumen = Länge mal Breite mal Höhe)

das Volumen 0.

Zeichnen wir nun die beiden Ergebnisse von A. und B. in ein Koordinatensystem ein:

Nun ändert sich zwischen diesen Extremwerten mit kontinuierlicher Veränderung des x auch das Volumen kontinuierlich (stetig), d.h. der Graph des Volumens ist als durchgezogener Strich zeichenbar, der zudem (weil zwischen den Extremwerten echte Volumina größer als Null entstehen) immer oberhalb der x-Achse liegt.

Man probiere verschiedene solcher Striche aus - und wird feststellen, dass

• notwendig verschieden große Volumina herauskommen, also nicht alle möglichen Schachteln dasselbe Volumen haben

(dann wäre die Aufgabe, nach einem Maximum zu suchen,  ja unsinnig oder zumindest doch grob irreführend), 

• auf jeden Fall mindestens ein Maximum zustande kommt, wir also später
  bei der Suche nach Maxima garantiert fündig werden:

Solches Springen von der Anwendung in rein mathematische Überlegungen und wieder zurück fordern den SchülerInneN sicherlich einige Flexibilität ab - und sollten dennoch immer wieder geübt werden.

zurück zu

 

Das Volumen V der jeweiligen Schachtel wird berechnet als

V = Schachtellänge mal Schachtelbreite mal Schachtelhöhe =

   =            a'               •                b'             •               x

Dabei ist V = a' • b' • x ist die erste Version unserer Zielfunktion, denn schließlich ist es unser Ziel, das Volumen zu maximieren.

Das Volumen V ist bislang von den drei Variablen a' , b' und x abhängig. Nun können wir aber nur mit Gleichungen rechnen, in denen nur eine einzige Variable vorkommt (üblicherweise x), und deshalb müssen aus der Gleichung V = a' • b' • x noch "irgendwie" die beiden Variablen a' und b' rausfliegen.

(... was wieder eine rein innermathematische Überlegung ist; das "Rausfliegen" kann aber wieder nur anhand der "Anwendung" erfolgen:) 

Um nun nicht in der Vielzahl der Variablen zu ertrinken, wird's spätestens jetzt Zeit, vorerst mal nicht von allgemeinen, sondern von konkreten Werten für die Papierlänge und -breite auszugehen.

(Wir werden unten aber auf den allgemeinen Fall zurückkommen!)

Der Einfachheit halber runden wir die Maße eines DIN-A4-Blattes sogar noch ein wenig auf:

• Papierlänge = 30 (cm)
• Papierbreite = 20 (cm)

Als "richtige" Mathematiker lassen wir zudem die cm-Einheiten vorläufig weg, wobei wir allerdings daran denken müssen,

• immer - was hier ja sowieso der Fall ist - nur mit denselben Einheiten zu rechnen und sie gegebenenfalls ineinander umzuwandeln

(also nicht gleichzeitig z.B. mit Zenti- und Kilometern zu rechnen), 

• ganz am Ende, also bei der Rückbeziehung des rechnerischen Ergebnisses auf die Anwendung, eben doch wieder die cm-Einheiten hinzuzufügen.

Mit den konkreten Maßen erhalten wir

Unser Ziel, nur noch die (einzige) Variable x zu haben, ist nur dadurch erreichbar, dass wir die beiden anderen Variablen a' und b' in Abhängigkeit von x darstellen können. Aus der letzten Zeichnung ergibt sich nun aber:

#         a' = 30 - 2x

# #      b' = 20 - 2x 

In diese beiden Gleichungen gehen also die konkreten Maße des Papiers bzw. sein konkreter Rand (Papierlänge, Papierbreite) ein, weshalb a' = 30 - 2x und b' = 20 - 2x auch "Randbedingungen" genannt werden.

(Die erste Aufgabe war überhaupt nur ausgewählt worden, weil da der Rand sehr handgreiflich mit dem Papierrand gleichgesetzt werden kann.)

Wenn wir nun die Ergebnisse aus # und # # in die erste Version der Zielfunktion einsetzen, so erhalten wir

V   =        a'      •      b'      • x =

      =  (30 - 2x) • (20 - 2x) • x

So kompliziert diese Gleichung auch noch aussehen mag, so hat sie doch immerhin den einen Vorteil, dass da überhaupt nur noch die (einzige) Variable x drin vorkommt, das Volumen also nur noch von x abhängig ist, so dass wir auch schreiben können:

       V (x) = (30 - 2x) • (20 - 2x) • x

Halten wir aber kurz inne:  

Wir brauchen die Randbedingungen, um Abhängigkeiten zwischen mehreren Variablen herzustellen und damit aus der Zielfunktion alle Variablen bis auf eine rauswerfen zu können. Die Randbedingungen sind zudem - insbesondere im Hinblick auf die Anwendung - nötig, damit nicht von irgendwelchen rechteckigen Blättern die Rede ist, sondern von einem konkreten (hier DIN-A4-großen).   (Wir werden allerdings unten bei der Balkenaufgabe sehen, dass man manchmal auch alle Balken "in einem Abwasch" erledigen kann, statt jede Balkengröße einzeln abzuarbeiten.)

 

Bislang haben wir viel auf das Anwendungsproblem geschielt und nur ab und zu "richtige" Mathematik betrieben. Nachdem nun aber die Zielfunktion V (x) = (30 - 2x) • (20 - 2x) • x steht, vergessen wir für einige Zeit völlig das Anwendungsproblem und beschäftigen uns rein innermathematisch mit dieser Zielfunktion.        (Man könnte auch sagen: jetzt folgt mit der klassischen Rechnung der langweilige Teil.)

Schauen wir uns nun die Funktion V (x) = (30 - 2x) • (20 - 2x) • x genauer an. Natürlich kann man sie durch Ausmultiplizieren in die Standardform V (x) = 4x³ - 100x² + 600x umformen

(wir werden das später auch tatsächlich brauchen).

Halten wir aber immerhin schon fest, was an 4x³ - 100x² + 600x  vielleicht doch leichter sichtbar ist als an (30 - 2x) • (20 - 2x) • x , dass nämlich eine Funktion dritten Grades vorliegt und somit der Funktionsgraph  ^̰-förmig ist.

Aber die ungewohnte Schreibweise V (x) = (30 - 2x) • (20 - 2x) • x hat durchaus ihre Vorteile:

angenommen, wir wollen

(wozu, wird später deutlich)

die Nullstellen dieser Funktion berechnen, also

0 = (30 - 2x) • (20 - 2x) • x

Weil der Gesamtterm (30 - 2x) • (20 - 2x) • x  als Produkt von Teiltermen vorliegt, also

0 = (30 - 2x) • (20 - 2x) • x ,

ist der Gesamtterm genau dann gleich 0, wenn einer der Teilterme gleich 0 ist, wenn also

(30 - 2x) = 0 oder  (20 - 2x) = 0 oder  x = 0

(... eine Argumentation, die nur mit 0 möglich ist! Vgl. ).

Das ist aber genau dann der Fall, wenn

          x = 15 oder              x = 10 oder x = 0   

Kommen wir damit zurück zu der Grafik

 

Die beiden Nullstellen x = 0 und x = = = 10 hatten wir schon oben als Randextrema entdeckt. Jetzt kommt noch die dritte Nullstelle x = 15 hinzu:

Eingedenk der Überlegung, dass eine Funktion dritten Grades vorliegt, die zwischen x = 0 und x = 10 ganz oberhalb der x-Achse verläuft, passt durch die Nullstellen aber nur (nicht maßstäblich) folgender Graph:

Daran ist zweierlei bemerkenswert:

1. liegt das gesuchte Volumenmaximum etwa bei 4, d.h. wir haben schon eine ungefähre Ahnung, was rechnerisch rauskommen muss; solch eine Ahnung ist aber immer gut, um später
   e (eventuell falsche) Rechenergebnisse einschätzen zu können;
   hinzu kommt, dass ungefähr bei 4 auch tatsächlich das Maximum und nicht etwa das Minimum liegt;
2. werden wir rechnerisch auch noch ein Minimum etwa bei 13 herausbekommen, das aber im Hinblick auf die angewandte Aufgabenstellung doppelt uninteressant ist:

• es ist ja gar nicht nach einem Minimum gesucht,
• wir hatten oben schon gesehen, dass x nicht größer als = = 10 sein, also nicht im hellblau markierten Bereich liegen darf, d.h. das Minimum kommt zwar mathematisch raus, ist aber im Hinblick auf die Anwendung gar nicht möglich.

Kleiner Exkurs:

es könnte wünschenswert erscheinen, sich mittels eines Funktionenplotters den Graph der Funktion V (x) = (30 - 2x) • (20 - 2x) • x = 4x³ - 100x² + 600x genau, d.h. auch maßstabsgetreu anzuschauen. Wegen der großen Zahlen 100 und 600 kommt dabei allerdings folgender wenig aussagekräftiger Graph heraus:

Nun aber zur schnöden Rechnung: um das Maximum  von V (x) = (30 - 2x) • (20 - 2x) • x = 4x³ - 100x² + 600x herauszufinden, leiten wir ab und setzen gleich 0.

V ' (x) = 12x² - 200x + 600 = 0   | : 12

                    x² -  x +   50 = 0

Daraus ergibt sich mit der Formel

x_1/2 =

Weil die Wurzel aus 700 irrational ist, ergeben sich leider unvermeidbar die ein wenig unschönen Werte

x₁ ≈ 3,9 und x₂ ≈ 12,7,

die aber immerhin den Vorteil haben, sehr nah an den oben abgeschätzten Werte x = 4 und x = 13 für die x-Werte des Maximums und des Minimums zu liegen.

Weil wir aber schon wissen, dass bei x₁ ≈ 3,9 nur das Maximum liegen kann, sparen wir uns die Bestätigung über die zweite Ableitung. Schon im Hinblick auf die Anwendung gesehen, bleibt also nur die Lösung x = übrig.

(Spätestens hier zeigt sich, dass die Überlegungen dazu, wie der Graph überhaupt aussehen kann und wo vermutlich das Maximum liegt, äußerst hilfreich sind:

• sie ersparen einige Rechnungen und damit Fehlermöglichkeiten
• und ermöglichen eine Einschätzung der [evtl. falschen] Rechenergebnisse.

Die Alternative ist, dass man blind rechnet und eben mit den Ergebnissen keinerlei Vorstellung mehr verbindet.

Nebenbei: an der Lösung ist leider nicht mehr zu erkennen, wie sie sich im Laufe der Rechnung aus den Anfangswerten a = 30 und b = 20 ergibt. In anderen Fällen lohnt es sich aber oft, dem Zustandekommen der Lösung innerhalb der Rechnung nachzugehen, wobei es ratsam ist, nicht mit Dezimalzahlen [Näherungen], sondern mit Brüchen und Wurzeln zu rechnen, zumal diese durch später
e Rechnungen oftmals wieder verschwinden und am Ende dann trotz schwieriger Zwischenwerte doch wieder einfache Ergebnisse zustande kommen.)

Nachdem wir uns lange in der reinen Mathematik rumgetrieben haben, müssen wir natürlich zurück zur Anwendungsaufgabe kommen, d.h. die Rechenergebnisse in diese zurück übersetzen.

Dazu machen wir uns nochmals zweierlei klar:

1. war die Schachtel mit maximalem Volumen gesucht,
2. war x die Seitenlänge der Quadrate, die an allen Ecken aus dem DIN-A4-Blatt  auszuschneiden waren.

Unsere erste Antwort lautet also (nun wieder unter Ergänzung der Maßeinheit cm):

Für die Schachtel mit maximalem Volumen sind aus dem DIN-A4-Blatt an allen Ecken Quadrate mit der Seitenlänge x = cm auszuschneiden.

Obwohl in der Aufgabenstellung nicht danach gefragt ist, stellt sich aber doch indirekt die Frage, wie groß das Volumen der Schachtel dann denn ist. Dazu setzen wir x =   in die Gleichung

 V (x) = 4()³ - 100 ⁽⁾² + 600 ()

ein und erhalten

V (     )   ≈ 875

(ich liefere nur die Näherung, da die Wurzeln nicht zu beseitigen sind).

bzw. nach (jetzt doch wieder) Ergänzung der Maßeinheit cm

V ( cm )   ≈ 875 cm.

Nun ist aber die erste Antwort 

Für die Schachtel mit maximalem Volumen sind aus dem DIN-A4-Blatt an allen Ecken Quadrate mit der Seitenlänge x = cm auszuschneiden.

bei der konkreten Herstellung der Schachtel unpraktikabel, denn wegen der Irrationalität der Wurzel aus 700 ist es völlig unmöglich, die Quadrate derart genau auszuschneiden

(man kann wohl nur auf einen Millimeter, also eine Nachkommastelle genau schneiden)

- und deshalb hatten die SchülerInnen auch von Anfang an keine Chance, exakt die Schachtel mit maximalem Volumen herzustellen.

Es darf also auf keinen Fall die rein theoretisch-mathematische erste Antwort stehen bleiben, sondern sie  muss auf die Anwendung hin verändert werden: 

Für die Schachtel mit maximalem Volumen sind aus dem DIN-A4-Blatt an allen Ecken Quadrate mit der Seitenlänge x = 3,9 cm auszuschneiden.

(... wobei mir hier, eben weil es um eine praktikable Antwort geht, durchaus das Gleichheitszeichen angebracht scheint.)

Des Weiteren wäre zu überlegen, ob die Lösung  x = 3,9 cm überhaupt sinnvoll ist. Angenommen nämlich mal, in die Schachtel der Länge 30 cm - 2 • 3,9 cm = 22,2 cm sollen Kugelschreiber der Länge 14 cm gelegt werden, so hat die Schachtel zwar (ausgehend von einem DIN-A4-Blatt) maximales Volumen, ist sie aber dennoch viel zu lang, wodurch sehr viel Leerraum entstünde. Die Schachtel wäre also eine Mogelpackung. Aber in diesem Fall würde man wohl kaum von einem DIN-A4-Blatt ausgehen, sondern von der Länge der Kugelschreiber (= Schachtellänge) und dem gewünschten Volumen, um davon ausgehend die günstigste Blattgröße zu berechnen.

2. Aufgabe: optimales Stadion

Eine andere schöne Aufgabe, in der sich die Randbedingung tatsächlich aus dem (Stadion-)Rand ergibt, ist die Stadionaufgabe in  .

In dieser Stadionaufgabe ist nebenbei auch - anders als in der 1. Aufgabe - sehr schön nachvollziehbar, wie sich die Lösungen und das erstaunlich einfache h = 100 m im Laufe der Rechnung aus der Randbedingung ergeben.

Kommt hinzu, dass in dieser Aufgabe - fast wie ein Wunder - das mathematische Ergebnis exakt mit den sportlichen Anforderungen übereinstimmt und vermutlich unmathematisch getroffene Entscheidungen auch mathematisch stützt.

3. Aufgabe: minimaler Blechverbrauch

Gesucht ist eine Konservendose, die bei einem Volumen von einem Liter aus möglichst wenig Blech hergestellt ist.

"möglichst wenig Blech" meint offensichtlich die Dosenoberfläche, und in "Volumen von einem Liter" ist das Volumen ja ausdrücklich angesprochen.

"möglichst wenig Dosenoberfläche" zeigt zudem an, dass die Oberfläche zu minimieren, also die Zielfunktion ist. Hingegen ist "Volumen von einem Liter" die zusätzlich nötige Randbedingung.

(Nebenbei: wenn wir im Folgenden die Volumeneinheit "Liter" weglassen, so müssen wir doch im Hinterkopf behalten, dass damit die Längeneinheit Dezimeter verbunden ist, da 1 dm • 1 dm • 1 dm = 1 Liter.)

Stellen wir deshalb - und zwar erstmal allgemein - die Formeln für die Dosenoberfläche 0 und ihr Volumen V auf:

• O = zwei Mal die kreisförmige Grundfläche (oben und unten) + einmal der rechteckige Mantel =

    =    2     •                               π r²                                               +                   h • 2  π r

• V = Grundfläche der Dose • Höhe =

   =                  π r²                •    h

Nun ist zusätzlich vorgegeben, dass das Dosenvolumen ein Liter sein soll, weshalb gilt:

1 =                   π r²                •    h

Diese Randbedingung hat wieder die typischen Eigenschaften: da nunmehr das Volumen nicht mehr variabel, sondern mit 1 festgelegt ist, also nicht mehr von allen möglichen Dosen (beliebigen Volumens), sondern nur noch denen (allerdings auch unendlich vielen) mit dem Volumen 1 die Rede ist, bleiben nur noch die beiden Variablen r und h übrig, so dass man sie in Abhängigkeit voneinander darstellen und dann aus der Oberflächenzielfunktion eine der beiden rauswerfen kann, so dass als einzige Variable nur noch die jeweils andere übrig bleibt.

Schauen wir uns gegenseitige Abhängigkeit von r und h in 1 = π r² •  h nochmals ein wenig genauer an:

da die Summe immer gleich, nämlich 1 sein soll, wird offensichtlich

• r immer größer, wenn h kleiner wird,
• r immer kleiner, wenn h größer wird.

Das trifft ja offensichtlich auch rein anschaulich zu: wenn beim vorgegebenen Volumen von einem Liter die Dose breiter (weniger breit) wird, so muss sie weniger hoch (höher) werden.

Die Gleichung 1 = π r² •  h formuliert nun aber diesen Zusammenhang nicht nur ungefähr (größer → irgendwie kleiner, kleiner → irgendwie größer), sondern exakt, nämlich z.B. so, dass r quadratisch, h hingegen nur linear in das Volumen eingeht, r also mehr bewirkt als h

(vgl. die Balkenaufgabe unten).

Normalerweise ist es egal, nach welcher Variablen man Randbedingungsgleichungen auflöst. Tun wir es hier mal sowohl für r als auch für h:

1. r =
2. h =

Setzen wir nun beide Variable in die Oberflächengleichung O = 2   π r²  +  h • 2  π r ein, so ergibt sich:

1. O = 2  π ( ) ²  +      h    • 2  π
2. O = 2   π       r    ²  +    • 2  π    r   

Damit ist in beiden Fällen das Ziel erreicht, dass nur noch jeweils eine Variable vorkommt und die Oberfläche nur noch von einer Variablen (im ersten Fall h, im zweiten r) abhängig ist, so dass wir auch schreiben können:

1. O (h) = 2  π ( ) ²  +      h    • 2  π
2. O (r) = 2   π       r    ²  +    • 2  π    r

Zudem können wir noch vereinfachen:

1. O (h) = 2  π         +      h    • 2  π
2. O (r) = 2   π       r    ²  +               2  •        =

                    =  2   π       r    ²  +               2  •    r ^-1

Üblicherweise besteht aber im Matheunterricht keine Möglichkeit, die Funktionsgleichung in a. und insbesondere nach h abzuleiten, was aber durchaus bei der Funktionsgleichung in b. möglich ist, die zudem viel einfacher aussieht.

In diesem Fall ist es also ungünstig, die Gleichung 1 = π r² •  h nach r aufzulösen (und damit r aus der Zielfunktion rauszuwerfen), bzw. viel günstiger, sie nach h aufzulösen (und damit h aus der Zielfunktion rauszuwerfen).

Wir bleiben also bei der zweiten Version der Zielfunktion, also

O   (r) =       2   π  r  ²  +        2  • r ^-1

Da es Ziel ist, die Oberfläche zu minimieren, müssen wir die  erste Ableitung bilden:

O ' (r) =  2 • 2 π  r  ¹  +  (-1) 2  • r ^-2 =

          =     4    π  r       -        2  • r ^-2

Wenn wir das gleich 0 setzen, ergibt sich:

              0  =     4    π  r       -        2  • r ^-2_,

und daraus wiederum folgt (hier abgekürzt) das in der Tat nicht gerade hübsche, weil irrationale Ergebnis

                r = ≈ 0,54

Fügen wir nun die Längeneinheit dm wieder hinzu, so ergibt sich  r ≈ 0,54 dm, d.h. die Dose mit minimalem Blechverbrauch hat einen Durchmesser von ungefähr 2 • 0,54 cm = 10,8 cm, und sie hat eine Höhe von ca. 10,9 cm.

Üblicherweise sehen Konservendosen aber so aus

,

sind also erheblich  höher als breit - und offensichtlich, wie eben gezeigt, Materialverschwendung. Ich habe aber keine Ahnung, weshalb man diesen Nachteil in Kauf nimmt.

Dennoch hört sich das Ergebnis d ≈ 10, 8 cm / h ≈ 10,9 cm ziemlich gut an: dass die Dose fast genauso breit wie hoch ist, erinnert doch sehr an den idealen Gegenstand für minimalen Materialverbrauch bei vorgegebenem Volumen, nämlich die Kugel

(die allerdings als Verpackung

• sehr schwer herzustellen,
• schlecht zu stapeln

[vgl. Keplers Packungsproblem] 

• und schlecht handhabbar ist

[kugelförmige Dosen würden immer aus dem Küchenschrank rollen und wären kaum ohne eine Riesensauerei zu öffnen.]).

4. Aufgabe:

Wie sieht ein Balken aus?

(Jan Peter Balkenende, niederländischer Ministerpräsident zumindest noch im Jahr 2008) "Warum kümmerst du dich um den Splitter im Auge deines Bruders oder deiner Schwester und bemerkst nicht den Balken in deinem eigenen? Wie kannst du zu deinem Bruder oder deiner Schwester sagen: Komm her, Bruder; komm her, Schwester; ich will dir den Splitter aus dem Auge ziehen, und merkst gar nicht, dass du selbst einen ganzen Balken im Auge hast? Scheinheilig bist du! Zieh doch erst den Balken aus deinem eigenen Auge, dann kannst du dich um den Splitter in einem anderen Auge kümmern!" (Lukas 6, 41f)

Darf man eine Aufgabe eigentlich derart offen stellen? Und wo ist da denn die eigentliche Aufgabe, d.h. was sollen die SchülerInnen tun - und auf die Dauer rechnen?

Umgekehrt ist aber doch die Entdeckung der Mathematik in einem anscheinend mathematikfreien Zusammenhang ein wichtiges Ziel, wenn man denn schon "Anwendungsaufgaben" durchnimmt.

(... wobei mir wie den SchülerInnen natürlich klar ist, dass arg suggestiv garantiert irgendwo Mathe lauert, wenn etwas im Mathematikunterricht durchgenommen wird.)