scheißegal
oder ohne Abstraktion läuft gar nix
oder was die Mathematik im Innersten zusammenhält

"Eines Tages nehme ich einen Fahrradsattel und eine Lenkstange und setze sie aufeinander. Ich mache einen Stierkopf. Sehr gut. Was ich aber sofort danach hätte tun sollen: den Stierkopf wegwerfen. Ihn auf die Straße, in den Rinnstein, irgendwohin werfen, aber wegwerfen. Dann käme ein Arbeiter vorbei, läse ihn auf und fände, daß man aus diesem Stierkopf vielleicht einen Fahrradsattel und eine Lenkstange machen könnte. Und er tut es. . . Wundervoll wäre das."
(Pablo Picasso)

Die konkreten Anlässe, beide am 13.9.07:

1. : in einer fünften Klasse ist laut Lehrbuch, Lehrplan & sämtlichen anderen versammelten Vorschriften das Thema "Schätzen & Runden" dran, und das ist ja ausnahmsweise sogar mal höchst sinnvoll

(wird in den Folgejahren viel zu selten gemacht).

Einige SchülerInnen gehen souverän an die Probleme ran

("ich denke mir die Bretter im Schrank weg und den Kugelschreiber eckig"),

während andere an der Realität kleben

(genau nachmessen, [aus mathematischer Sicht] Spitzfindigkeiten einbringen ...).

Fast könnte man sich fragen, welche der beiden Schüler"sorten" bereits "verdorbener" ist.

Zeigen sich da nur verschiedene Entwicklungsstufen

(die zweite Gruppe wird sehr bald auch das Abstrahieren lernen),

oder wird da sehr früh klar, wer nie ein guter Mathematiker werden wird

(wobei ich mich allerdings mit Händen und Füßen gegen solch eine frühe Einsortierung wehre)?

In der 5. Klasse geht es zudem um sehr große Zahlen, die sich schnell eben beim Abschätzen ergeben können. Beispielsweise wurde in der betreffenden Klasse berechnet, wie viele Einzeltische "so ungefähr" in den Klassenraum passen, wenn

• man sie nicht nur neben- und hintereinander stellt, sondern auch stapelt,
• ein Tisch  "der Einfachheit halber" ca. 50 cm ● 50 cm ● 50 cm groß ist,
• der Raum

(und es ist ausnahmsweise wirklich mal ein sehr großer Raum, also nicht so eine typische Schüler-Legebatterie)

"intelligent gerundet" 10 m ( Länge) ● 5 m (Breite) ● 5 m (Höhe) groß ist.

Es ergibt sich:

• eine Reihe von 10 Tischen nebeneinander in der Breite;
• 20 solche Reihen hintereinander in der Länge, womit der Boden vollständig zugestellt ist. Und solch eine "Lage" besteht immerhin schon aus 200 Tischen!
• In der Höhe 10 solche "Lagen" übereinander, so dass nun endlich der Raum vollständig gefüllt ist. Und das sind nun tatsächlich (auch für mich!) vollends unanschaulich-abstrakte 2000 Tische.

Wie aber geht man mit solcher Abstraktheit um?:

1. Man könnte sie folgendermaßen zu veranschaulichen versuchen:

• Das Ergebnis 2000 besagt, dass man "im Prinzip" sämtliche SchülerInnen der Schule in diesem einen Raum unterbringen, alle anderen Räume vermieten und alle anderen Lehrer entlassen könnte!

(Das als kleiner Vorschlag, um an Schulen wirklich effizient Geld zu sparen.)

• Weil der Raum vollständig mit Tischen (auch übereinander gestapelt) ist, kann natürlich kein Schüler mehr "an"/hinter seinem Tisch sitzen, und deshalb wurden tatsächlich mal Tische gestapelt und haben sich einige Schüler "unter" ihren jeweiligen Tisch, aber auf den Tisch des "Unter-Mieters" gesetzt.

Ich meine tatsächlich, dass solche Überlegungen folgen müssen, man also das Ergebnis nicht einfach hinnehmen und damit völlig abstrakt (eben Mathematik) bleiben lassen darf.

Und dennoch:

2. Solche Überlegungen können letztlich nur bzw. immerhin das Staunen erhöhen (überhaupt erst erzeugen?). Das Ergebnis bleibt auf diese Art aber unvorstellbar-abstrakt.
3. Hilfreicher wäre höchstens ein Modell

(denn man wird aus technischen und Zeitgründen ja wohl kaum 2000 echte Tische in der Schule zusammenklauben und dann in dem einen Raum stapeln können).

In diesem Modell würden z.B. 2000 Würfel

(woher nehmen, wenn nicht stehlen?)

reihen- und lagenweise in ein Raum-Modell gepackt, d.h. die Reihen und Lagen nicht nur "gedacht", sondern sukzessive wirklich aufgefüllt.

"Unsereins" ist ja fähig, ausgehend von einem einzigen Tisch den gesamten Raum virtuell und systematisch (eine Reihe, mehrere Reihen = eine Lage, mehrere Lagen) mit "Tischen" anzufüllen:

Aber solche virtuellen Fähigkeiten muss man anfangs doch mal anhand der Wirklichkeit oder von Modellen üben, also z.B., indem man anfangs immerhin einige Tische/Würfel reiht und stapelt und erst danach den Raum weiter "volldenken" lässt.

2. : am Klassenraum einer 9. Klasse steht zufällig die Tür offen. Drinnen befindet sich der Mathelehrer gerade mit den SchülerInneN in einer hitzigen Diskussion darüber, "wozu man der ganze Quatsch [Wurzelrechnung] überhaupt braucht".

Der Lehrer argumentiert zuerst auf einer völlig falschen Ebene, nämlich mit vermeintlich alltäglichen Anwendungsproblemen, die die SchülerInnen nicht haben und nie haben werden.

Zunehmend in die Enge getrieben, wird der Lehrer dann aber doch "ehrlicher" und sagt so etwa sinngemäß, der Anlass (Wurzeln) sei doch "(scheiß-)egal"

(so derbe hat er sich allerdings nicht ausgedrückt),

sondern es gehe um grundsätzliche .

(Und fast schon lustig fand ich, dass er dann mit "meinem" zweiten Fach Deutsch verglich: wenn der "Sturm & Drang" dran sei, sei es doch auch [scheiß-]egal, an welchem Werk man ihn exemplifiziere.)

Könnte darin der Konflikt begründet liegen?:

vielen SchülerInnen ist die Mathematik scheißegal, weil der Mathematik so viel scheißegal ist.

Ich werde nie behaupten, dass meine Gedanken völlig neu sind:

1. sind sie (vermutlich) sowieso keine Weltneuheiten. Beispielsweise haben schon die Reformpädagogen vor rund 100 Jahren 90 % aller guten pädagogischen Ideen abgegrast.
2. ergänzen sich meine Essays bzw. differenzieren sie sich zunehmend (zu Tode?) aus.

   Über die Unvermeidbarkeit, aber auch Notwendigkeit, ja sogar Schönheit von Abstraktion in der Mathematik habe ich ja schon oft laut nachgedacht, nämlich z.B. in

• ,
• ,
• ...

Manchmal wird mir aber auch erst sehr spät siedend heiß klar, was ich vorher nur ungefähr angedacht hatte. Hier also: mir geht erst jetzt auf, dass nicht bloß, arg allgemein gesagt, Mathematik Abstraktion IST, sondern

Und manchmal widerspreche ich mir sogar gerne selbst

(was dann nicht bloß ein Schein-Widerspruch ist, aus dem ich mich doch wieder "irgendwie" mit einer windelweichen "Synthese" rauswinden werde):

Beispielsweise würde ich zwar nicht so weit gehen, die "propädeutischen" Ansätze in und als Schnickschnack zu bezeichnen, sondern sie mögen anfangs ja durchaus sinnvoll sein, damit die SchülerInnen mit Brüchen überhaupt eine Anschauung verbinden.

Aber mit und ist natürlich das eigentliche Problem, dass die SchülerInnen nämlich auf Dauer abstrakt mit Brüchen umgehen können müssen (s.u.), noch lange nicht gelöst, bzw. das "missing link" dahin fehlt noch völlig

(... oder zumindest doch weitgehend: sicherlich kann massenhaftes Rechnen mit Brüchen, also schlichtes "Pauken", teilweise dafür sorgen, dass Rechnungen automatisiert und damit Brüche abstrakt werden - und doch geht genau dieses Standardverfahren offensichtlich allzu oft schief: ein paar Monate später können viele SchülerInnen trotz massenhaften Rechnens gar nichts mehr).

Und dann habe ich doch Selbstbewusstsein genug, zwischen

1. meinem Grundansatz und
2. der soeben immerhin schon angedeuteten Dominanz der Abstraktion

keinen Widerspruch zu sehen.

Beispielsweise dient

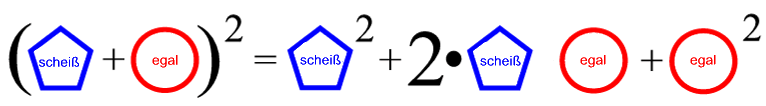
ja eben gerade der Förderung der Abstraktionsfähigkeit und klebt keineswegs an irgendeiner die Abstraktion oftmals geradezu verhindernden "Anwendbarkeit"

(vgl. ).

Man kann sich (als LehrerIn) gar nicht deutlich genug klar machen, dass im Matheunterricht fast alles abstrakt ist. Und das ist einem oftmals gerade deshalb nicht (mehr) bewusst, weil es einem allzu selbstverständlich ist

(weil man in dieser Abstraktheit schwimmt wie der Fisch im Wasser; und vielleicht weiß der Fisch gar nicht [mehr], dass er sich in Wasser bewegt)

- aber den SchülerInneN nicht!

• Beretis die angeblich "natürlichen" Zahlen sind so natürlich ja gar nicht, sondern schon erhebliche Abstraktionen:

drei Fische, drei Bäume, drei BMWs, drei Kuscheltiere  3

Das einzige, was z.B. drei Bäume und drei Kuscheltiere gemeinsam haben, ist eben die 3

(im Grund haben wir da eine Zuordnung betrieben, nämlich jedem Baum ein Kuscheltier zugeordnet und dabei 3 bereits völlig abstrakte Zuordnungspfeile erhalten).

Und in der Tat wird dann im Unterricht ja nicht mehr von Fischen, Bäumen, BMWs oder Kuscheltieren, sondern nurmehr von der splitterfasernackten Abstraktion 3 gesprochen.

• Sogar die "Grundgesetze" der Mathematik sind

(eben als allgemeine Gesetze)

völlig abstrakt:

• Kommutativgesetz:
  •                   scheiß + egal = egal + scheiß,
  •                   scheiß  • egal = egal •  scheiß,
• Distributivgesetz:
  • sowieso • (scheiß + egal) =  sowieso • scheiß + sowieso • egal,
• Assoziativgesetz:
  • sowieso + (scheiß + egal  = (sowieso + scheiß) + egal,
  • sowieso •  (scheiß •  egal) = (sowieso •  scheiß) • egal.

• Gleiches gilt, wie bereits oben gesagt, für die "Binomis":

• Bei den oben bereits erwähnten Brüchen ist eine Anschauung letztlich sogar kontrakproduktiv.

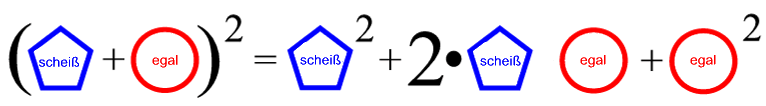
Ein Laie wird vermutlich noch einsehen, wozu man sehr einfache Brüche braucht, also z.B. :

Anno dunnemals bestellte man beim Metzger noch nicht mit (Kilo-)Gramm-Angaben, sondern z.B.

"ich hätte gern Pfund (darf´s ein bisschen mehr sein?)."

Aber der Laie wird schon nicht mehr einsehen, wozu "schwierigere" Brüche da sind

(und "schwieriger" bzw. ohne jede Anwendung sind alle Brüche, bei denen Zähler oder Nenner größer als 4 sind: kein Mensch redet im Alltag beispielsweise von Fünfteln).

Für solch "schwierigere" Brüche muss ich nichtmal beispielsweise zu greifen, sondern da reicht bereits z.B. .

Nichtmal Mathematiker haben von irgendeine genauere Vorstellung - und schon gar nicht vom exakten (?) "Zahlenwert"  1,30769230769231.

An diesem exakten (?) Zahlenwert wird der Unterschied zwischen "richtigen" Mathematikern einerseits und Laien andererseits sogar besonders gut deutlich:

• Laien (SchülerInnen) greifen, weil sie sich (wie auch Mathematiker!) nichts unter vorstellen können, sofort zum Taschenrechner, um eine Vorstellung, nämlich 1,30769230769231, zu bekommen. Aber was ist das bei den vielen Nachkommastellen für eine Vorstellung?! Sie wird doch nie genauer als 1,3.
• Mathematiker hingegen wollen´s so genau gar nicht wissen - und wissen doch viel mehr:

1. wissen sie ohne Rechnen oder gar Taschenrechnereinsatz sofort, dass irgendwo (das muss reichen!) zwischen 1 und 2 liegt, weil 17 größer als 13, aber kleiner als das (noch leicht zu berechnende) 2-fache von 13 (also als 26) ist.
2. können Mathematiker aber je nach Lust und Laune umgekehrt auch richtig fies genau werden: 1,30769230769231 ist eben nicht der absolut exakte "Zahlenwert", sondern der Taschenrechner hat Nachkommastellen abgeschnitten und zudem gerundet (die 1 am Ende!). Die Mathematiker wissen also - nochmals: ohne jedes Rechnen oder Taschenrechnereinsatz -, dass das Taschenrechenergebnis sogar - genau genommen - falsch ist. Denn weil ein Bruch aus ganzen Zahlen ist, muss der "Zahlenwert" hinter dem Komma endlich oder aber periodisch sein. Und ein Mathematiker wird eben wissen, dass beim Nenner 13 eine Periode zu erwarten und dementsprechend

= 1,307692 307692 307692 307692 ... = 1,307692

ist. Genau genommen wissen Mathematiker, dass da eine Periode folgt, aber nicht, welche, und Letzteres ist ihnen auch herzhaft egal.

Und all das (nicht die einzelnen Nachkommastellen, aber die Periodizität) wissen unsere "richtigen" Mathematiker eben, ohne überhaupt  den Taschenrechner bemühen zu müssen (den sie letztlich sowieso verachten).

• Noch deutlicher wird das bei Wurzeln: bereits bei der

(abgesehen von den trivialen Fällen = 0 und = 1)

einfachsten nur denkbaren Wurzel, nämlich , weiß sowohl ein Laie als auch ein Mathematiker doch höchstens, dass

≈ 1,41 und ein paar Gequetschte.

Nun weiß ein Mathematiker allerdings noch zusätzlich, dass eine irrationale Zahl ist

(vgl. ),

was doch bedeutet:

• ist in der Dezimalschreibweise weder endlich noch periodisch hinter dem Komma, also völlig chaotisch, woraus folgt:
• es lohnt nicht, ja ist völlig aussichtslos, die Dezimalschreibweise von zu berechnen (vom Taschenrechner berechnen zu lassen).
• Bis hierhin klingt das rein resignativ: was soll man denn dann mit anfangen? Aber unser Mathematiker findet es eben gerade äußerst faszinierend, dass laut Definition von das Quadrat dieser völlig chaotischen Zahl doch wieder das ganz simple Ergebnis 2 hat:

()² = 2

Oder allgemeiner:

()² = scheiß

Man muss also nicht im mindesten wissen, was in Dezimalschreibweise ist, und kann dennoch prächtig damit (mit Scheiß[e]!) hantieren

("er hat mal wieder voll in die Scheiße gepackt").

Und um kurz auf diesem fallweise existentiellen oder vulgären Niveau zu bleiben: man kann mit Scheiß(e) machen, was man will (Wurzelziehen, Quadrieren), es bleibt Scheiß(e) bzw. wird oftmals sogar nur noch mehr Scheiß(e).

• Und spätestens Variable und dann allgemeine Funktionsvorschriften

(und damit endlich 90 % der Schulmathematik)

sind vollständige Abstraktionen, denn beispielsweise

y = x²

bedeutet doch nichts anderes als

scheiß = egal².

Die Gleichung ist universell, d.h. es ist scheißegal, was ich für "egal" einsetze. Bei "scheiß" habe ich dann allerdings keine Wahl mehr, sondern die Gleichung gibt rigide vor, auf welche Art (hier: Quadrieren) sich aus dem "egal" der "SCHEISS" ERGIBT.

(Helmut Kohl: "Entscheidend ist, was hinten rauskommt.")

Man könnte auch sagen, dass Mathematiker sich nicht für die (Einzel-)"Dinge", sondern "nur" für die Beziehungen zwischen ihnen interessieren.

• Zuguterletzt noch ein Beispiel aus der Geometrie bzw. genauer zu

  oder ,

  nämlich der berühmt-berüchtigte Satz des Pythagoras, an dem die Anwendbarkeit MathematikerInnen doch am allerwenigsten interessiert:

  sowieso ² + scheiß ² = egal ²

  Allerdings ist daran eine Sache NICHT scheißegal

(genauso, wie laut Relativitätstheorie eben NICHT alles relativ, sondern die fixe Lichtgeschwindigkeit "das Maß aller Dinge" ist):

der Satz des Pythagoras gilt nur in rechtwinkligen Dreiecken, von denen es aber auch wieder sozusagen scheißegal (unendlich) viele gibt.

Und beim scheißegal-Verallgemeinerungswahn der Mathematiker stellt sich dann natürlich schnell die Frage, wie es mit

sowieso ³ + scheiß ³ = egal ³

sowieso ⁴ + scheiß ⁴ = egal ⁴

usw., also

sowieso ^scheißegal + scheiß ^scheißegal = egal ^scheißegal

(wobei allerdings die "scheiß" und die "egal" im Exponenten nicht dieselben sein müssen wie die in den Basen),

also mit steht.

Spätestens hier wird es Zeit, das höchst illustrative, aber eben auch potentiell anbiedernd-vulgäre scheißegal-Niveau zu verlassen:

Es müsste klar geworden sein:

1. ist die Abstraktion nicht bloß wünschenswertes Ziel des Matheunterrichts, sondern von Anfang an (und nicht erst in der Universitätsmathematik) ihr unvermeidbar fundamentaler Bestandteil. Man könnte fast sagen:

auch schon Schulmathematik IST Abstraktion bzw. "scheißegal", bzw. es ist die Abstraktion, die die (Schul-)Mathematik im Innersten zusammenhält.

2. den SchülerInnen wird also ebenso unvermeidbar ständig Enormes abverlangt, d.h. ihre Schwierigkeiten sind unausweichlich und vorprogrammiert.

Wie aber mit diesen Schwierigkeiten umgehen? Ein erster Ansatz ist zweifelsohne , aber der reicht nicht aus und führt nicht allzu weit, ja drückt sich vielleicht sogar um die eigentliche Schwierigkeit, nämlich den "Sprung" in die Abstraktion.

Da könnte man fragen, ob dieser "Sprung", diese - mathematisch gesagt - "Unstetigkeitsstelle" überhaupt methodisch-didaktisch planbar ist.

Zumindest scheint man mir im üblichen Unterricht mangels methodisch-didaktischer Alternativen darauf zu vertrauen, dass die SchülerInnen beim vielfachem Üben und zunehmend automatisiertem Rechnen irgendwann von selbst und spontan diesen Quantensprung vollziehen

(der eine früher, der andere später - und einige nie?),

und seien wir ehrlich: irgendwann hat´s auch bei uns "Klick" gemacht, aber der Zeitpunkt, an dem dieses geschah, ist gar nicht mehr zu verorten.