das Ende der mathematischen "Strenge"

Also lautet ein Beschluss:
Daß der Mensch was lernen muss.
Nicht allein das Abc
Bringt den Menschen in die Höh';
Nicht allein in Schreiben, Lesen
Übt sich ein vernünftig Wesen;
Nicht allein in Rechnungssachen
Soll der Mensch sich Mühe machen;
Sondern auch der Weisheit Lehren
Muss man mit Vergnügen hören.
Dass dies mit Verstand geschah,
War Herr Lehrer Lämpel da.

Max und Moritz, diese beiden,
Mochten ihn darum nicht leiden,
Denn wer böse Streiche macht,
Gibt nicht auf den Lehrer acht.

Nichtmathematiker werden bei "Strenge" eher unangenehm berührt an eine stramm autoritäre Erziehung denken, etwa im Sinne von

streng, strikt, drastisch, massiv, rigoros, rigide, energisch, entschieden, bestimmt, mit erhobenem Zeigefinger, mit sanfter Gewalt, hart, scharf, rücksichtslos; einschneidend, gravierend, herrisch, rücksichtslos, unbarmherzig, unzugänglich; streng werden, ein Machtwort sprechen, mit der Faust auf den Tisch schlagen / hauen; strenger werden, die Zügel straffer anziehen; streng behandeln, jemanden an die Kandare nehmen; eingreifen; Unerbittlichkeit.
(Dudenverlag)

Und das Substantiv definiert der Duden sogar kurz und knapp als

Strenge Unerbittlichkeit.

Bei mathematischer Strenge wird der Laie also wohl an denken.

Vor allem impliziert für mich "Strenge" aber immer: auf keinen Fall lachen!

Dabei hat "mathematische Strenge" aber primär eine ganz andere, rein fachliche

(?, weil dennoch mit der pädagogischen Strenge ursächlich zusammenhängende?)

Bedeutung.

Unter mathematischer Strenge versteht man - einfach gesagt - eine glasklar (und eiskalt!) logische Vorgehensweise, wie sie vielleicht schon

Euklid in seinen (fatalen?) "Elementen"

"Die Grundthese dieses Vortrags ist, dass die frühe Entstehung der Elemente von Euklid für die Entwicklung der Didaktik ein Hindernis gewesen ist. Deswegen sind die Möglichkeiten zum Entstehen eines informellen, intuitiven Beginns des Geometrieunterrichts blockiert worden. Trotzdem haben viele Mathematiker und Didaktiker im Laufe der Geschichte oft empfohlen, den Geometrieunterricht, auch schon für kleine Kinder, mit einem informellen Einstieg anzufangen. Verschiedene unter ihnen haben auch wirklich versucht, einen solchen Lehrgang zu entwickeln."
(über einen Vortrag von Dr. Ed de Moor vom Freudenthal-Insitut in Utrecht/NL)

Endgültig festgezurrt wurde diese Strenge dann aber spätestens im 19. Jahrhundert von Cauchy, Gauß und Weierstraß.

Oder exakter:

"Wir erörtern noch kurz, welche berechtigten allgemeinen Forderungen an die Lösung eines mathematischen Problems zu stellen sind: ich meine vor allem die, daß es gelingt, die Richtigkeit der Antwort durch eine endliche Anzahl von Schlüssen darzutun, und zwar auf Grund einer endlichen Anzahl von Voraussetzungen, welche in der Problemstellung liegen und die jedesmal genau zu formulieren sind. Diese Forderung der logischen Deduktion mittels einer endlichen Anzahl von Schlüssen ist nichts anderes als die Forderung der Strenge in der Beweisführung. In der Tat, die Forderung der Strenge, die in der Mathematik bekanntlich von sprichwörtlicher Bedeutung geworden ist, entspricht einem allgemeinen philosophischen Bedürfnis unseres Verstandes, und andererseits kommt durch ihre Erfüllung allein erst der gedankliche Inhalt und die Fruchtbarkeit des Problems zur vollen Geltung. Ein neues Problem, zumal, wenn es aus der äußeren Erscheinungswelt stammt, ist wie ein junges Reis, welches nur gedeiht und Früchte trägt, wenn es auf den alten Stamm, den sicheren Besitzstand unseres mathematischen Wissens, sorgfältig und nach den strengen Kunstregeln des Gärtners aufgepfropft wird.
Zudem ist es ein Irrtum zu glauben, daß die Strenge in der Beweisführung die Feindin der Einfachheit wäre. An zahlreichen Beispielen finden wir im Gegenteil bestätigt, daß die strenge Methode auch zugleich die einfachere und leichter faßliche ist. Das Streben nach Strenge zwingt uns eben zur Auffindung einfacherer Schlußweisen; auch bahnt es uns häufig den Weg zu Methoden, die entwicklungsfähiger sind als die alten Methoden von geringerer Strenge."
(David Hilbert, 1862 - 1943; vgl. )

Solche (mathematische) Strenge hat allemal immense Vorteile:

• überhaupt erst sie (die Absicherung der Fundamente sowie die Klärung der logischen Verfahren) hat zu rasanten Fortschritten in der Mathematik geführt;
• durch sie werden zahlreiche (u.a. logische) Fallgruben vermieden;
• sie ist eben nicht automatisch mit "Schwierigkeit" gleich zu setzen, sondern vereinfacht auch vieles (s.o. Hilberts zweiter Absatz); d.h. sie erspart auch SchülerInnen heute noch viele Probleme;
• sie ist eine gute "Schule des Denkens" oder genauer: einer bestimmten Art des Denkens;
  ja, vielleicht ist dieses Denken sogar weit über die Mathematik hinaus bedeutsam - und gehört Mathematik gerade oder überhaupt erst deshalb (und weniger um ihrer selbst willen) in die "Allgemeinbildung": Mathematik als Bollwerk gegen das Geschwafel, ja sogar als Ideologiekritik:

"Moralisch [!] lehrt uns die Mathematik, sich streng [!] gegenüber dem zu verhalten, was als Wahrheit behauptet wird, was als Argument hervorgebracht wird oder was als Beweis angeführt wird. Die Mathematik fordert Klarheit der Begriffe und Behauptungen und duldet keinen Nebel und keine unbeweisbaren Erklärungen."
(A. D. Alexandrow)

(Aber fördert diese mathematisch Denkstringenz nicht auch - s.u. - einseitiges Denken?);

• vor allem aber hat diese "Strenge" ja durchaus auch ihren ästhetischen Reiz

(wenn das auch eine sehr kühle, vielleicht sogar unmenschliche Ästhetik ist):

wie sich da teilweise in höchster Eleganz zack-peng-boing erstaunliche Ergebnisse scheinbar von selbst ergeben und wie überhaupt alles aus einem einzigen Stamm (vgl. wieder Hilbert) zu erwachsen scheint.

Und doch hat die mathematische Strenge auch fatale Nachteile gezeitigt, nämlich

• der Mathematik alles Leben (u.a. ihrer Erfinder und Entdecker) ausgetrieben

(vgl. ),

• durch ihre Geschichtslosigkeit alle kulturellen Wurzeln der Mathematik gekappt

• insbesondere zu einer völligen Enthistorisierung der Mathematik selbst geführt, und zwar vor allem in den Augen der sekundäre Charge, die nicht wahrhaben will und kann:

"Allerdings ist die mathematische Strenge nicht absolut. Sie entwickelt sich, ihre Prinzipien sind nicht ein für allemal fest, sondern bewegen sich und sind ebenfalls Objekte wissenschaftlicher Diskussionen."
(A. D. Alexandrow)

• - eben doch als historische Reflexe der jeweiligen Epochen - zu einer ebenso abstoßenden wie fatalen Mischung aus Fortschrittsgläubigkeit, Rechthaberei und Arroganz geführt:

"Keinerlei [!] Glaubwürdigkeit ist in jenen Wissenschaften, die sich der mathematischen Wissenschaften nicht bedienen oder keine Verbindungen zu ihnen haben."
(Leonardo da Vinci)

"Diese Überzeugung von der Löslichkeit eines jeden mathematischen Problems ist uns ein kräftiger Ansporn während der Arbeit; wir hören in uns den steten Zuruf: Da ist das Problem, suche die Lösung. Du kannst sie durch reines Denken finden; denn in der Mathematik gibt es kein Ignorabimus [= wir werden es nie wissen]!"

(wieder Hilbert, der allerdings persönlich keineswegs so "streng" war).

Da empfindet man doch fast schon eine "klammheimliche Genugtuung"  , dass Kurt Gödel(1906 - 1978) an die Fundamente dieses vermeintlich "unkaputtbaren" Gebäudes eine hübsche kleine Bombe gelegt hat, was ich (auch wenn ich´s, ehrlich gesagt, nicht ganz verstehe) keineswegs als Katastrophe, sondern als Befreiung und Ermutigung empfinde:

"Der destruktive Charakter kennt nur eine Parole: Platz schaffen; nur eine Tätigkeit: räumen. Sein Bedürfnis nach frischer Luft und freiem Raum ist stärker als jeder Haß."

(Walter Benjamin)

• Die mathematische Strenge hat die Mathematik u.a. eben auch zu einem Tummelplatz für sekundäre Kleingeister und "Sachwalter" der "einzig wahren Lehre" (formal-logischen "Sauberkeit") gemacht, die sich (was sie dringend verbergen und sich nicht eingestehen können) verzweifelt an etwas festklammern müssen

"Mein teurer Freund, ich rat Euch drum
Zuerst Collegium Logicum.
Da wird der Geist Euch wohl dressiert,
In spanische Stiefel eingeschnürt,
Daß er bedächtiger so fortan
Hinschleiche die Gedankenbahn."
(Goethe, Faust)

Hier aber geht es mir um Schulmathematik.

Wie schon oben gezeigt, kann kein Zweifel bestehen, dass die mathematische Strenge viele Vorteile hat. Aber sie darf nicht vorausgesetzt bzw. unverstanden eingebläut werden, sondern

• muss sicherlich ab und zu sozusagen zum Schutz der SchülerInnen vor allzu vielen Umwegen eingefordert (also auch vorher geübt) werden,
• sollte aber doch vor allem sukzessive als Wert entdeckt werden:

So aber sieht die Schulmathematik bislang keineswegs aus, sondern

• die Schulbücher sind immer schon tertiärer Aufguss der Strenge, ja die Autoren sichern sich immer - also von der Mathematik, nicht der Pädagogik aus - gegen alle "strengen" Einwände ab, sind also mehr für FachkollegInnEn als SchülerInnen geschrieben;
• allzu viele MathematiklehrerInnen verstehen sich (ausschließlich) als MathematiklehrerInnen, also FachwissenschaftlerInnen, und nicht als MathematiklehrerInnen.

"Mathe ist bei uns [...] ein Problemfach. Die Mathelehrer interpretieren [unseren pädagogischen Ansatz] weniger unter dem Aspekt des problemorientierten Lernens [worunter man ja auch innermathematische Probleme verstehen kann] als unter dem Aspekt der [innerfachlichen] Effektivität und Computerisierung der Mathematik."
(aus einem anonymisierten Email)

Insbesondere ertragen viele MathelehrerInnen keine Sekunde eine vorläufige, probeweise mal ungenaue oder umgangssprachliche Terminologie, bzw. die "strenge" Sprache ist oftmals ihr einziges Ziel:

• was wurde mir im Referendariat durch meine heißgeliebte Fachleiterin das Leben schwer gemacht, weil ich die SchülerInnen nicht aufforderte:

"Zeichnet im Punkt P(3|y) eine Tangente an den Graphen der Funktion mit der Funktionsgleichung y = x² "
(wenn man so redet, braucht man dreimal so lang und werden die SchülerInnen endgültig konfus)

sondern sagte:

"Zeichnet da eine Tangente";

• viele MathematiklehrerInnen kriegen die Krätze, wenn man sagt:

  • Stetigkeit bedeutet, dass die Kurve in "einem Wusch" zeichenbar ist,

  • Differenzierbarkeit bedeutet, dass die Kurve "keinen Knick in der Optik" hat,
    Differenzierbarkeit ist "weiblich"-wohlgerundet
    (igitt, Sexismus und zudem unsachlich!).

  Nein, ohne ε-Kritierum ist das für sie überhaupt keine Mathematik.

Dabei ist gerade die umgangssprachliche Terminologie sehr wichtig: sie allein bettet das mathematisch zu Lernende in die Alltagserfahrungen ein (bzw. geht von diesen aus), macht es also anschaulich.

Eigentlich ist Fachsprache doch - wie ein Linguist sagen würde - erst arbiträr (willkürlich) und dann konventionell (für alle verpflichtend), d.h. selbstverständlich hätte man das "Assoziativgesetz" auch "Schnurps-" oder - wie ich ja durchaus sinnvoll finde - "Zuordnungs-" bzw. "Klammerverschiebungsgesetz" nennen können:

(oder weil ich mir ja zu keiner Veranschaulichung zu schade bin: es gehen wohl mal a und b und zu anderer Zeit b und c "miteinander ins Bett", nie aber alle drei gleichzeitig;

um kurz auf solchem Niveau zu bleiben:

• das Kommutativgesetz a + b = b + a bzw. a ● b = b ● a besagt, dass mal a, mal b "oben liegt" bzw. im Bett Gleichberechtigung herrscht;

• und das Distributivgesetz a ● (b + c) = a ● b + a ● c besagt, dass a es mit b und c gleichzeitig "treibt" [aber b nicht mit c].)

(Vgl. etwa im Deutschunterricht die Verwechslungen zwischen den ähnlich klingenden Wörtern "Subjekt" und "Substantiv": für letzteres wäre "Hauptwort" eben vielleicht doch besser.)

Nun bedeutet das lateinische Wort "Assoz-" ja in der Tat so etwa "Zuordnung", aber das hilft SchülerInnen spätestens dann nicht mehr, wenn sie kein Latein mehr können (und auch das deutsche Fremdwort "assoziieren" nicht mehr kennen).

Hier aber kommt der konventionelle Teil ins Spiel: wenn das Assoziativgesetz nunmal traditionell so genannt wird, kann man vielleicht noch kurzfristig im eigenen Unterricht aus dieser Sprachregelung heraus, wird aber eben auch das konventionelle Fachwort üben müssen, damit die SchülerInnen sich auch später mit Mathematik(lehrer)InneN verständigen können.

Wenn also beispielsweise Enzensberger in seinem Buch spaßeshalber mal von "Rettich" statt von "Wurzel" und von "hopsen" statt vom abstrakten "Potenzieren"  ( ?) spricht, so wird diese Sprachregelung sicherlich auf sein Buch beschränkt bleiben, zumal zumindest "Rettich" ja auch nicht besser (anschaulicher, verständlicher) als "Wurzel" ist. Wenn Enzensberger mit dem - ja offensichtlich von "Wurzel" abgeleiteten - "Rettich" überhaupt was erreicht hat, dann, dass die verblasste Metapher "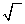" endlich mal wieder (wie bei allen Metaphern nötig) wörtlich genommen und damit das Wurzelziehen als Tätigkeit (statt als Computerergebnis) verstanden wird.

Fachsprache ist ja durchaus "sinnig":

1. wurden die Begriffe meist eben keineswegs völlig willkürlich gewählt ("Schnurpsgesetz"), sondern machen durchaus Sinn bzw. beschreiben kurz, was da vorliegt

("Assoz-" = "Zuordnung"; oder die "Punktrichtungsform" einer Geraden geht eben gerade davon aus, dass eine Gerade in diesem Fall allein durch einen Punkt auf ihr und ihre Richtung festgelegt werden kann).

Es wäre nur dringend nötig, solche Entsprechungen von Bezeichnungen (Signifikanten) und mathematischen Gegenständen ("Signifikaten") ausdrücklich durchzunehmen und zu veranschaulichen.

2. tragen Fachbegriffe dazu bei, sich Sachverhalte zu merken und sie erkennen zu können:

Wer beispielsweise mal ausführlich Metaphern im Deutschunterricht durchgenommen und sich das Wort gemerkt hat, wird sie auch leichter in einem Text finden, und vom Begriff aus geht dann eine ganze Reiz-Reaktions-Kette (Interpretation) aus.

Fachsprache ist also eine Art "Geländer", das man manchmal von SchülerInnen (u.a. zu ihrer eigenen Sicherheit) einfordern muss, auch wenn das ihnen gegenüber nicht immer motivierbar ist.

Leider werden Fachbegriffe im Unterricht aber oftmals völlig sinnentleert und stur angewandt

(wobei die sture Anwendung manchmal ja durchaus dazu beiträgt, einmal richtig begriffene Vorgehensweisen zu automatisieren).

Das beste Beispiel sind da Äquivalenzzeichen

(da Symbole ja auch sprachliche Zeichen sind bzw. alle Sprache nur aus Symbolen besteht):

• SchülerInnen setzen sie - wenn von der Lehrkraft gefordert - oft gnadenlos und ohne jedes Verständnis: "wenn der Lehrer sie unbedingt haben will, dann kriegt er sie ebe, und notfalls würden wir, und notfalls würden wir sieunsssogar auf die Backe tätowieren lassen";sogar auf die Backe tätowieren lassen";
• das Beste, was man da noch sagen kann, ist, dass die SchülerInnen damit auch keine Fehler machen, denn bei den allermeisten Gleichungsumformungen, die sie durchführen, kann man ja auch tatsächlich ununterbrochen Äquivalenzzeichen setzen;

• bis zum Ausnahmefall der Wurzelgleichungen in der 9. Klasse lernen die SchülerInnen in der Regel überhaupt keine Ausnahmen bzw. Sonderfälle kennen - und ist also das Äquivalenzzeichen gleichermaßen selbstverständlich wie überflüssig;

• in der 9. Klasse werden dann tatsächlich mal diese Ausnahmen bei Wurzelgleichungen behandelt (ja, die Wurzelgleichungen werden in der Regel überhaupt nur deshalb durchgenommen), aber das bleibt Strohfeuer, und danach kommt immer wieder nur der Regelfall.
• genau da liegt das Problem: es werden ja auch fast nur solche Gleichungsumformungen durchgenommen, bei denen sich zwischen erster und letzter Zeile die Lösungsmenge nicht ändert. Oder genauer:

Wenn also Äquivalenzzeichen sinnig sein sollen, so bleiben nur vier Möglichkeiten:

• entweder kommen immer mal wieder mittendrin auch Ausnahmen vor

(Veränderung der Lösungsmenge im Laufe von Rechnungen; oder genauer natürlich: wie erreicht man, dass die Lösungsmenge sich nicht verändert?);

• oder der Sinn von Äquivalenzzeichen  wird anderweitig verständlich gemacht, nämlich dadurch, dass
• alle Umformungen nur dazu dienen, die Anfangsgleichung (Aufgabenstellung) zu lösen,
• das Ziel darin liegt, die in der Anfangsgleichung noch versteckte Variable in der letzten Gleichung sichtbar zu machen (vgl. ),
• zwischendurch Rechenfehler (deren Vermeidung ja nun tatsächlich im Interesse der SchülerInnen liegt!) stattgefunden haben können und deshalb das Ergebnis in der letzten Zeile zur Probe in die Anfangszeile eingesetzt werden muss (d.h. die Probe muss Regel und [fast] immer mit eingefordert werden).

(evtl. auch auf Selbstverständliches wie z.B. 3 = 3 oder 3 ≠ 4):

Schwieriges ... ... Einfaches

Das ist doch nur dann "sinnig", wenn man am Ende auch wieder lückenlos rückwärts schließen kann:

Schwieriges ... ... Einfaches

• Ein weiterer wichtiger Anlass, über Äquivalenzzeichen nachzudenken, scheint mir der Übergang zu (Taschenrechner-)Näherungswerten:

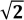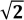
x ² = 2 x = oder x = - x ≈ 1,4142 oder x ≈ - 1,4142

Aber aus  x ≈ 1,4142 oder x ≈ - 1,4142 folgt nicht rückwärts auch wieder x² = 2, denn (+/-1,4142)² ≈1,9999616 ≠ 2: die Äquivalenzkette ist an einer Stelle (bei  ) unterbrochen.

Man könnte auch sagen: ist eine "semipermeable Membran", die Dinge nur von links nach rechts (raus) durchlässt, aber nicht rückwärts (rein):

hingegen ist eine Drehtür, zu der man rein und raus kann:

Bzw. => ist ein Informationsfilter, bei dem einige Informationen endgültig verloren gehen. Z.B. kann ich, wenn ich erst mal beim Rundungsergebnis 1,4142 bin, nie wieder weitere Nachkommastellen der 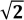berechnen

(und irgendwann mag sich bei technischen Anwendungen ja die Notwendigkeit einer größeren Genauigkeit ergeben; bzw. weitere Rechnungen mit 1,4142 statt 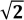können einen anfangs kleinen Rundungsfehler derart "aufblähen", dass das Endergebnis der Rechnung völlig unbrauchbar ist - weshalb es meist sinnvoll ist, möglichstmöglichst lange in einer Rechnung mitzuschleppen [insbesondere dann, wenn später doch wieder quadriert wird] und überhaupt erst ganz am Ende den Dezimalwert zu berechnen).

MathematikerInnen interessiert in der Regel nur totale Äquivalenz, aber nicht die Reduktion auf einige Details (und dann der naive oder dreiste Rückschluss aufs Ganze), die ja in der Tat gemeingefährlich werden kann

(z.B. beim Rückschluss von der [vermeintlichen] Eigenschaft eines Individuums auf eine ganze Menschen"rasse").

D.h. Mathematik erzeugt eine gesunde Allergie gegen unzulässige Verallgemeinerungen und Rückschlüsse

(macht aber auch schnell blind dafür, dass es im "richtigen" Leben kaum allgemeingültige Regeln gibt; bzw. allzu leichtfertig aufs "Leben" übertragen, stülpt sie diesem oft leichtfertig und dann auch gefährlich allgemeine Regeln über).

Manchmal ist der Verlust von Informationen aber auch wünschenswert,

• wenn man nicht in der Fülle der Informationen ertrinken will

(so dass man vor lauter Bäumen den Wald nicht mehr sieht)

• oder einen sowieso nur ein bestimmtes Detail interessiert.

 Am Beispiel der :

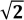• für viele Anwendungen braucht man gar nicht so viele Nachkommastellen: etwa dann, wenn man ein Brett sowieso nur auf Millimeter genau sägen kann;
•  man möchte endlich eine Vorstellung (nicht ein genaues Ergebnis) davon bekommen, welche Größenordnung 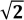hat. An 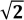sieht man das ja überhaupt nicht

(oder wenn überhaupt, dass der Zahlenwert irgendwo zwischen 1 und 2 liegen muss),

bei 1,4142 hat man aber schon genauere Vorstellungen.

Werden wir ENDLICH "un-strenger", also anschaulicher !   Eine Schulmathematik, die die "Strenge" übertreibt bzw. sich nur daran misst, macht sich nur zum Lakaien des derzeit gängigen Sozialdarwinismus, sie ist nur - nochmals gesagt - .