"so ungefähr" oder "genau"

Beide Witze zusammen verraten viel über MathematikerInnen - aber auch über grundsätzliche Probleme von Laien/SchülerInneN.

Denn in der Tat ist die Aussage

"π ist die Zahl, die das Verhältnis zwischen dem Umfang eines Kreises und seinem Durchmesser angibt"

(im Gegensatz zu "π ist 3,1415927 plus/minus 0,00000005" oder gar "π ist ungefähr 3")

2. absolut exakt und

3. (zumindest auf den ersten Blick) völlig unnütz.

MathematikerInnen tun etwas völlig Schizophrenes:

• einerseits können sie (erstaunlich genug!) beweisen, dass π eine "irrationale" Zahl, d.h. in Dezimalschreibweise nach dem Komma weder endlich noch periodisch ist, d.h. sie können durchaus etwas sehr Genaues über π bzw. all seine (unendlich vielen!) Nachkommastellen sagen,

• andererseits beweisen sie damit aber auch, dass man π niemals komplett in Dezimalschreibweise aufschreiben kann - und geben damit jeden Versuch, es dennoch zu tun, umgehend und konsequent auf: weil sie nicht alles können, tun sie gar nichts - und geben sich mit der einzig exakten Möglichkeit, nämlich der Umschreibung "Verhältnis zwischen dem Umfang eines Kreises und seinem Durchmesser", zufrieden.

(Ganz ähnlich ist es mit der ebenfalls irrationalen : da es aussichtslos ist, ihre Dezimalstellen aufschreiben zu wollen, merken sich MathematikerInnen nur das einzige, was tatsächlich exakt über sagbar ist, nämlich dass ()² = 2 ist. Das reicht für alle innermathematischen Belange, und einE "richtigeR" MathematikerIn wird den Teufel tun, sich viele Nachkommastellen, also z.B.  1.4142135623731, zu merken oder gar einen Taschenrechner anzuschalten, um das herauszufinden. Aber immerhin kennt jedeR MathematikerIn wohl noch die ersten paar Nachkommastellen der berühmtesten Wurzel, also von , nämlich 1,4142. Aber beispielsweise bei kennt sie/er nichtmal mehr diese Nachkommastellen, sondern reicht ihr/ihm einzig und allein ()² = 17.)

Allerdings ist "völlig unnütz" nicht ganz korrekt: woher denn hat der Physiker seine Näherung "3,1415927 plus/minus 0,00000005"? Doch wohl von MathematikerInneN, denn diese können zwar

(wie sie ja bewiesen haben)

nicht alle (unendlich viele!) Nachkommastellen von π berechnen, aber immerhin doch Algorithmen (Rechenverfahren) angeben, mit denen man beliebig viele Stellen von π nach dem Komma berechnen kann - oder genauer: könnte. Denn den "richtigen" Mathematiker interessiert ja nur, dass es solche Algorithmen gibt, aber das stumpfe Rechnen, das zur Bestimmung z.B. von 100 Nachkommastellen von π nötig wäre, hasst ein "richtiger" Mathematiker natürlich wie die Pest

(ist unter seiner Würde)

und überlässt er doch lieber dem Rechenknecht = Computer.

MathematikerInnen setzen aber sogar noch eins drauf und argumentieren gerne folgendermaßen: weil

(wie sie ja bewiesen haben)

π niemals exakt

(als Dezimalzahl)

aufzuschreiben ist, gibt es dieses π gar nicht vorweg, sondern definieren sie es überhaupt erst als die Zahl (den "Grenzwert"), gegen die ein Algorithmus "konvergieren" würde, wenn man ihn immer länger und länger anwenden würde

(welch nette Konjunktive!).

Es ist ja gerade der Gag einer Definition, dass es das, was da definiert wird, vorher gar nicht gab, sondern erst durch die Definition erschaffen wird.

(Man könnte fast sagen: wenn es Gott nicht gibt bzw. wenn er nicht "fassbar" ist, definieren sich die MathematikerInnen ihn einfach - durch unendliche Annäherung.

Ein anderes, mathematisches Beispiel: bei der Einführung der Differentialrechnung wird die Tangente an eine Parabel in einem Punkt gesucht. Natürlich kann man diese Tangente "so ungefähr" an die Parabel legen, aber welche der folgenden beiden ist denn die exakte Tangente: die blaue oder die violette?:

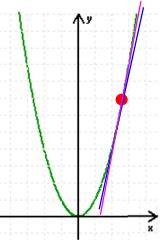
Da es nur den einen "Haltepunkt" • gibt, lässt sich mathematisch [auf diese Art] überhaupt nicht die exakte Tangente bestimmen, sondern bleibt alles ein ziemlich "wabbeliges" Ausprobieren nach Augenmaß. Und da es so also gar nicht geht, sagen die MathematikerInneN einfach, dass es diese Tangente gar nicht gibt, sondern sie erst als Grenzwert eines anderen, nämlich des Sekanten-Verfahrens entsteht. Dieses andere Verfahren funktioniert nun aber durch Annäherung mittels zweier Punkte • und •  , zu denen immer jeweils exakt eine Geradengleichung aufstellbar ist:

)

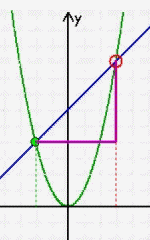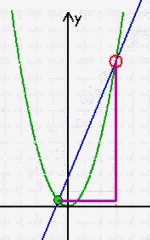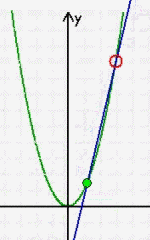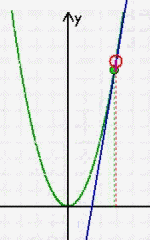Spätestens solch eine eingeschwurbelte Argumentation ist aber dem klischeehaften Physiker

(und erst recht dem Ingenieur)

herzhaft egal, wenn nicht gar wesensfremd:

• was sollen solche Überlegungen über Unmögliches?

• "so genau woll'n wa's doch gar nicht wissen",

• "mir reichen die halbwegs exakten Rechenverfahren, die die Mathematik uns Physikern (bzw. Ingenieuren) zur Verfügung stellt, aber es interessiert mich nicht die Bohne, wie sie zustande kommen; oder anders gesagt: die Mathematik ist mir eine Hilfswissenschaft, deren Feinheiten (oder gar Absurditäten) mir gestohlen bleiben können."

Und genau diese Einstellung haben auch

(ich möchte fast sagen: naturgemäß)

die allermeisten SchülerInnen

(um die es mir ja viel mehr geht als um Physiker und Ingenieure):

ihnen ist die stumpfe und oftmals sogar verhasste Rechnerei allemal noch lieber als die eigentlich mathematischen Überlegungen, und in der Tat sagen sie oft, wenn man mal in einer Klausur abfragt:

"Können wir nicht einfach wieder »richtig« [nach vorgegebenen Rezepten] rechnen?"

Der Übergang von solch einer Einstellung zur "richtigen" (!) Mathematik erscheint mir aber wie ein Quantensprung, und das meine ich sowohl im physikalischen als auch im umgangssprachlichen Sinn:

"In kleinsten (atomaren und subatomaren) physikalischen Systemen sind die Übergänge zwischen den Zuständen nicht kontinuierlich sondern immer quantisiert [d.h. in minimalen, oftmals zufälligen Sprüngen ohne Zwischenzustände] . Somit beschreibt der Begriff Quantensprung nichts besonderes, sondern Quantensprünge sind die einzig möglichen Zustandsänderungen in solchen Systemen. Da sich die Quantenmechanik mit atomaren und subatomaren Systemen befasst, sind diese Übergänge zudem sehr klein. Einfach gesagt ist ein Quantensprung also die kleinstmögliche Zustandsänderung in einem physikalischen System.

Außerhalb der Physik wird heute oft von einem Quantensprung gesprochen, wenn von einem großen oder ungewöhnlichen Fortschritt die Rede ist. Dieses Verständnis ist genau das Gegenteil der eigentlichen physikalischen Bedeutung des Begriffs. Es ist unklar, wie und wann diese falsche Metapher Eingang in die Alltagssprache gefunden hat."
(Quelle: )

Im physikalischen Sinne ist der Übergang zur "richtigen" Mathematik also ein vielleicht klitzekleiner, aber auf jeden Fall urplötzlicher Sprung, der sich

(so glaube bzw. befürchte ich)

nicht pädagogisch planen lässt und irgendwann von einigen SchülerInneN vollzogen wird - und von vielen nie.

Und man kann sich streiten, ob dieser Sprung großartig oder eine eher mickrig

(bzw. aus Physiker-, Ingenieurs- bzw. Laiensicht unnötig oder gar "pervers")

ist. Aus mathematischer Sicht ist er auf jeden Fall enorm wichtig, ja, mit ihm fängt die (eigentliche) Mathematik überhaupt erst an:

("for mankind"??? - auf jeden Fall aber für die Mathematik!!!)