wirklich verstehen

"Ich weiß nicht, was mit den Leuten ist: sie lernen nicht durch Verstehen; sie lernen irgendwie anders – durch Auswendiglernen oder so. Ihr Wissen ist so leicht zu erschüttern!"

(Richard Feynman, Nobelpreisträger für Physik; in gewissem Sinne ist oder tut er blöder als alle anderen: er kann einfach nicht verstehen, was für viele andere selbstverständlich ist: ein Auswendiglernen ohne echtes Verständnis)

Wirkliches Verstehen (Durchdringen) erfolgt in der Mathematik wohl (wie in vielen anderen Fächern auch) auf vielfältige und gleichzeitige Weisen.

Dabei mag subjektive Veranlagung eine Rolle spielen: der eine ist nunmal ein eher "optischer", der andere ein eher "akustischer" Lerntyp. Aber vermutlich denkt und lernt jeder meistens "synästhetisch", also durch Kombination der Lernverfahren. Und (SchülerInnen-)Gruppen sind sowieso "synästhetisch" zu "versorgen", damit jedeR sich die individuell beste Lernart aussuchen kann.

Wichtige Arten des Verstehens sind:

1. soweit wie möglich Anschaulichkeit

ggf. auch an vereinfachenden Modellen, die ja oftmals wiederum ein erhellendes Licht auf die Theorie zurückwerfen, also keineswegs nur sekundärer Luxus sind.

Dabei muß es sich gar nicht wortwörtlich optisch um AnSCHAUung handeln, sondern können - ganz im Sinne o.g. Synästhesien - z.B. auch akustische Verdeutlichungen stattfinden.

Mir scheint z.B., daß viele Mathematiker Formeln auch als Melodie verstehen, also z.B. einen Term mit dem Beginn der "Kleinen Nachtmusik" von Mozart:

Vielleicht wird einem erst durch schnelleren Rhythmus klar, daß (mittels Klammer) 5 und x, nicht aber 7 und 5 zusammengehören.

An"schau"lichkeit kann auch heißen, Mathematikmodelle selbst (also haptisch) zu basteln: aufgrund der mechanischen und räumlichen Probleme (auch Fehlversuche, ja, manchmal sogar Unmöglichkeiten) findet man überhaupt erst die logischen Strukturen eines mathematischen Sachverhalts heraus. Ich kann mir also durchaus eine AG "wir basteln Mathe-Modelle" vorstellen.

Z.B. ist mir überhaupt erst beim Bau eines Kathetensatz-Beweismodells aufgegangen, wie simpel und elegant, ja geradezu "natürlich" dieser Beweis ist (aber erstmal drauf kommen!):

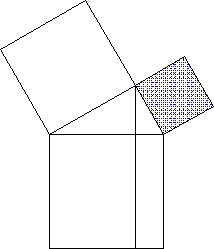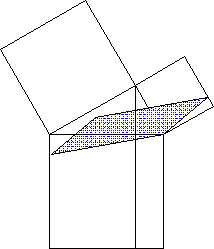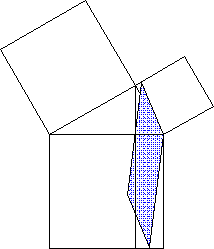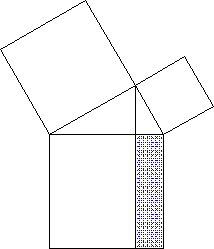
2. Gewöhnung durch Gebrauch

Selbstverständlich behält das pure Pauken und Rechnen (das, was ich immer "Etüden" nenne) seinen Wert.

Z.B. das Distributivgesetz [also a · ( b + c) = a · b + a · c] behält man nicht dadurch, daß man es einmal lernt, und auch nicht dadurch, daß es vielleicht einmal erstklassig anschaulich gemacht wird.

Sondern man behält es erst (ja, es wird erst verstanden und zur "zweiten Haut"), wenn man es massenhaft angewandt und vor allem (jenseits eines Beweises) bemerkt hat: "das Ding funktioniert immer, egal, was ich für a und b und c einsetze".

Es ist wirklich so: erst nach ewigem Umgang mit einer Sache bemerkt man erstaunt, daß einen die anfänglichen Schwierigkeiten verlassen haben.

Solches Sich-immer-wieder-an-einer-Sache-Abarbeiten funktioniert genauso, wie ein amerikanischer Professor Deutsch gelernt hat: nicht mit einem Sprachbuch (und abstrakten Regeln), sondern indem er immer wieder das Buch "Hotzenplotz" von Otfried Preußler gelesen und eine Tonkassette dazu gehört hat, indem er also wie ein Kind gelernt hat: beim immer selben doch immer neue Details.

Anders gesagt: Pauken und Wiederholen sind nicht (nur) Schikanen, sondern durchaus auch kindgemäß.

Und dennoch vertrauen Lehrer oftmals allzu leichtfertig auf das pure Pauken, das doch auch einen eminenten Nachteil hat: daß da etwas zwar andauernd angewandt wird, aber nie verstanden (fast hätte ich gesagt: an Gefühl und Rhythmus [s.o] gekoppelt) wurde; und daß es deshalb auch oft falsch angewandt wird.

3. inneres Verständnis eines Sachverhalts jenseits der bloßen Rechnens

Als der Quantenphysiker Heisenberg eine erste (von ihm selbst erstellte) mathematische Fassung (also simple mathematische Symbole) der neuen Atomtheorie auf dem Papier sah, war er

"[...] zutiefst erschrocken. Ich hatte das Gefühl, durch die Oberfläche der atomaren Erscheinungen [und der mathematischen Symbole!] hindurch auf einen tief darunter liegenden Grund von merkwürdiger innerer Schönheit zu schauen."

Die mathematischen Symbole sind für ihn durchsichtig auf echte Anschauung hin geworden. Es ist wie bei der Lektüre eines spannenden Romans: hinter der puren Druckerschwärze und Anhäufung von Buchstaben und Wörtern geht ein Bild auf.

Dann wird beispielsweise bei der Buchstaben-/Zahlkombination x² automatisch immer die Form eine Parabel mitgedacht, und das Kommutativgesetz a + b = b + a wird tatsächlich erlebt:

vermutlich funktioniert es so:

"es bleibt sich im Endeffekt gleich, ob ich erst 3 Äpfel und dann 4 Birnen oder umgekehrt erst 4 Birnen und dann 3 Äpfel kaufe" ist

• für den Anfänger ein konkreter Einstieg ins allgemeine Kommutativgesetz,

• für den geübten Mathematiker nur eine Veräußerlichung des längst stattgefundenen inneren Erlebnisses.

Nehmen wir als Beispiel den mathematischen Super-GAU, die Division DURCH NULL. Sie passiert andauernd, wenn SchülerInnen einfach nur gnadenlos drauflos rechnen und die durchaus verstandenen Regeln ebenso gnadenlos anwenden. Oder sie passiert, wenn das Kürzen nicht verstanden wurde, also statt zu 1 zu 0 ("gar nichts") gekürzt wird.

Denn viele SchülerInnen rechnen ja nach dem Motto "denn sie wissen nicht, was sie tun".

Verhinderbar wäre die Division durch Null, wenn SchülerInnen bei Bruchrechnung immer an Kuchen und Leute dächten. Irgendwann verschwinden dann sicherlich diese äußeren Bilder und funktioniert es - mit gleicher Anschaulichkeit! - auch nur mit Zahlen (und später dann sogar nur mit Variablen; aber selbst da ist denkbar: a/b bedeutet a Kuchen an b Leute; und irgendwann - wohl durch Gewöhnung und doch den schwierigsten Schritt - verschwinden dann sogar die Kuchen/Leute und ist ein Zähler/Nenner genauso anschaulich).

Mit "Kuchen und Leuten" bedeutet 2/3 dann 2 Kuchen an 3 Leute, 3/2 hingegen 3 Kuchen an 2 Leute (wobei offensichtlich jeder mehr bekommt).

0/3 bedeutet dann 0 Kuchen an 2 Leute, also bekommt jeder 0 Kuchen. 0/3 = 0. Man darf also Null durchaus durch etwas (eben außer Null) dividieren!

3/0 hingegen bedeutet 3 Kuchen an 0 Leute. Das aber ist unter der wichtigen Voraussetzung, daß die Kuchen immer irgendwo (bei irgendwelchen Leuten) bleiben MÜSSEN, unmöglich. Anders gesagt: wenn der Lehrer 3 Kuchen mitbringt und sie an keineN SchülerIn (0 Leute) verteilt, bleiben sie dennoch irgendwo, nämlich beim Lehrer (der auch 1 "Leut" ist). Es gilt also nicht 3/0, sondern 3/1 = 3. Der Lehrer ißt alle drei Kuchen ganz allein.

Mit der Division durch Null muß weniger Anschaulichkeit und (nicht vorhandene) Anwendbarkeit verbunden werden als eine negative Emotion (der Lehrer ist egoistisch und gibt nichts ab) bzw. Allergie.

Deshalb ja können Lehrer gar nicht genug Anekdoten erzählen und Bilder verwenden.

Oder man müßte SchülerInnen mal die dramatischen Prozesse vorführen, die in einem Taschrechner oder Computer vor sich gehen, dem man die Division durch Null befiehlt und der keine "Error"-Sicherung hat (daß diese Sicherung in Taschenrechner eingebaut ist, könnte ein entscheidender pädagogischer Fehler sein). Was bedeutet denn "Programmabsturz"?

Zum inneren Verständnis gehört auch die Frage: was kann (vor allem Rechnen oder auch unabhängig von ihm) eigentlich bei einer Aufgabe rauskommen - so daß man später ein eventuell falsches rechnerisches Ergebnis (und wer verrechnet sich nicht ab und zu?) anhand dieses Vorverständnisses überhaupt erkennen kann?

Vielleicht sollte man nie wieder eine Aufgabe lösen (lassen), ohne vorher zu überlegen, was dabei überhaupt und gerundet rauskommen kann, und nachher mit dieser anfänglichen Vermutung zu vergleichen. Von Interesse wären da auch die Fälle, in denen einen die anfängliche Vermutung irreführt und die Mathematik einen eines besseren belehrt (was ich immer "die Mathematik als eine Sonde in eine andere Wirklichkeit" bzw. "gehirnausrenkend" nenne).

Ebenso wäre öfter zu fragen, wie bestimmte Ergebnisse zustande kommen, an welcher Stelle der Rechnung also bestimmte Effekte auftauchen.

Beispiel:

dass die Wendepunkte einer komplizierten Funktionenschar dritten Grades im unten graphisch vorliegenden Fall hübsch auf einer Geraden (also dem Graphen einer Funktion ersten Grades) liegen, "sieht" man erst, wenn nacheinander viele Funktionsgraphen mit jeweils eingezeichneten Wendepunkten erscheinen

 - und dann erst stellt sich die Frage, weshalb das (algebraisch) so ist, an welcher Stelle der Berechnungen also die dritte Potenz in eine erste, lineare Potenz "zusammenschrumpft".

Oder (und damit ist der eben genannte Effekt schon geortet): warum reduziert die Ableitung den Exponenten so hübsch um exakt Eins? Und wenn das eruiert ist, sollte man den Unterricht (mitten in der Stunde!) beenden und vor lauter Freude über solche Einfachheit und Genialität eine Orgie veranstalten, also MATHEMATIK FEIERN.

Könnte es gar sein, daß wir an Schulen durch die (allemal wichtige!) Betonung von Rechenfertigkeiten und Anwendung von Verfahren (Zwischenschritte, richtiges Ergebnis) geradezu vom inneren Verständnis ablenken?:

"Eines stieß Paul an der Schule ab: daß man dort seinerzeit größten Wert auf schnelles Lösen numerischer Probleme legte; zwei banale Rechenfehler in einer Arbeit (gegen die Uhr), und man hatte sie verhauen, egal, ob man die gestellten Aufgabengrundsätzlich verstand oder nicht. Das Drexel-Institut versuchte damals, sich einen Ruf als harte, leistungsorientierte Anstalt zu schaffen, und war stolz auf seine hohe Abbrecherquote. Die Lehrer trichterten den angehenden Ingenieuren ein, daß ihre zukünftigen Arbeitgeber nur solche Mitarbeiter wollten, die schnell und richtig rechnen konnten. Zu seiner Bestürzung mußte Paul miterleben, daß die »machohafte« Einstellung der Schule zur Mathematik viele intelligente, kreative Freunde zwang, das Handtuch zu werfen."

(die Rede ist von Paul Baran, immerhin einem der führenden technischen Köpfe bei der Erfindung des Internets)

4. Strukturen der Wissenschaft, Position eines Sachverhalts in der Gesamtstruktur

Im Unterricht sind Zusammenhänge immer wieder ausdrücklich zu betonen und überhaupt erst herzustellen. Nur so bleibt das Einzelfaktum nicht isoliert, sondern findet Platz und Notwendigkeit in der Gesamtstruktur der Mathematik.

Ich sage also schon Sechtkläßlern öfters, wo ihr derzeitiger Stoff später nochmal wichtig sein wird

(und habe nebenbei meinen ganzen Stoff überhaupt nur nach zwei Kriterien organisiert:

• entweder er wird später nochmal wichtig,

• oder er erbringt wichtige mathematische Denkweisen).

Und ich nehme mit Sechtkläßlern bei der Bruchrechnung auch schon mal kurz Beispiele irrationaler Zahlen (eigentlich erst Stoff der 9. Klasse) durch, also z.B. 0, 1 0 1 00 1 000 1 0000 .... Also Zahlenbeispiele, bei denen vielleicht sogar Sechtkläßlern "aufgehen" kann, daß sie erstaunlicherweise (!!!) weder endlich noch periodisch (also nicht als Brüche ganzer Zahlen) darstellbar sind.

Und umgekehrt erinnere ich SchülerInnen der 9. Klasse an ihre Vorarbeiten (auf die sie stolz sein können!) in der 6. Klasse.

Zudem werden erst durch Vergleich typische mathematische Strukturen und Denkweisen deutlich, die wiederum auf das Einzelfaktum (und sein Verständnis) zurückwirken: z.B. die Verallgemeinerung von 1, 2, 3 ... auf n hat man erst wirklich verstanden, wenn man sie an vielen, äußerlich sehr unterschiedlichen Fällen gesehen, ja, wenn man bemerkt hat, daß Verallgemeinerung ganz grundsätzlich ein abgrundtiefer Mathematiker-Wunsch ist.

Um exemplarisch auf die Bruchrechnung und irrationale Zahlen zurückzukommen: vielleicht gewinnt erst (nachträglich!) ein intuitives Verständnis der Brüche (ihrer besonderen Praktikabilität, ja, Schönheit), wer später auch die "so widerlichen" irrationalen Zahlen kennengelernt hat.

Und gleichzeitig sind irrationale Zahlen doch wunderhübsch:

1. allemal geeignet, wieder mal lustvoll ein geistiges Gefängnis (eben das der rationalen, also ach so  "vernünftigen" Zahlen) aufzubrechen,

2. so herzhaft einfach: man darf nur eben nicht bei der Bruchrechnung stehen geblieben sein (insbesondere im Zeitalter des Taschenrechners bzw. Computers, der ja einfach zu blöd für irrationale Zahlen ist), sondern muß die ungeheure Faszination bemerkt haben, daß z.B. die Wurzel aus 2 zwar nicht (nicht genau; und das ist das einzige Kriterium für Mathematik) in Dezimalschreibweise darstellbar und dennoch ganz simpel ist:

das Einzige, was "man" über die Wurzel aus 2 weiß (und was in der formalen Darstellung √2 so genial kodiert ist), ist doch

• einerseits, daß ihr Dezimalwert herzhaft scheißegal ist,

• andererseits, daß ihr Quadrat erstaunlicherweise exakt (also millimetergenau) wieder 2 ergibt!

Man muss sich selbst (als ausgebildetem Mathematiker) das mal wirklich fassungslos klarmachen, um überhaupt SchülerInnen zu verstehen bzw. entgegen zu kommen:

da multipliziert man eine aberwitzig irrationale Zahl (nämlich √2 = 1,4142...) mit einer anderen aberwitzig irrationalen Zahl (nochmals Ö2);

und bei solch blödsinniger Multiplikation kommt erstaunlicherweise exakt (auf eine Milliarden und noch mehr Nachkommastellen) die simpel einfache, nämlich ganze Zahl 2 raus!!!!?:

√2 · √2 = 2 !!!!!!!!!!!

Was die SchülerInnen im Regelfall nicht kapiert haben (und was wir eben nicht "beigebracht" haben), ist was ganz Simples:

• dass √2 und 1,4142... DASSELBE, d.h. nur verschiedene Darstellungen derselben Zahl sind;

• dass also z.B. auch 

2 = √4 = 2/1 = 4/2 = 8/4 = 2,00000000......

immer dasselbe, immer dieselbe Zahl ist

(etwa so, wie die je nach Sprache verschiedenen Signifikate [Wörter für eine Sache]

[das deutsche Wort "Tisch" und das englische Wort "table"]

denselben Signfikanten [das Ding "an sich"], nämlich den Gegenstand "Tisch" meinen.)

Und wenn´s um wahrhaft pädagogische Diskussionen geht, dann eben nicht um Computer und anderen Schnickschnack, sondern um solch ganz simple - und fatale - Verständnisprobleme!

Und ich bin wahrhaft stolz drauf, als Nicht-Mathematiker noch oder wieder solche pädagogisch abgrundtief elementaren Fragen stellen zu können!

5. Nachvollzug der Entdeckungsgeschichte

Sie hat den großen Vorteil, daß sie exemplarisch vorführt, wie man überhaupt zu Erkenntnissen kommen kann, welche Schwierigkeiten sie aber auch bereiten. D.h., im Grunde ist sie eine Kopie des derzeitigen Laien, der genauso dumm und schlau wie der damalige Fachmann ist.

Zudem können anhand der Entdeckungsgeschichte besonders gut typisch mathematische Denkweisen klargemacht werden. Nehmen wir nur mal das Beispiel der Riemannschen Geometrie:

• einerseits Loslösung von der Anschaulichkeit,

• andererseits später eben doch Anwendbarkeit.

Oder einfacher die negativen Zahlen:

• erst große Ablehnung allerseits,

• inzwischen problemloser Umgang mit ihnen auch bei Laien.

Und dann Vergleich der beiden Themen (Riemannsche Geometrie/negative Zahlen), eben gerade weil "wir" (Laien heute) die negativen Zahlen problemlos, die Riemannsche Geometrie aber noch lange nicht "gegessen" (also anschaulich bekommen) haben.

Und ein interessantes Rätsel ist es allemal auch, ob wir jemals ein Sensorium für Riemannsche Geometrie bekommen werden.

Zweifelsohne sollte "wirklich verstehen" immer Anspruch an den Unterricht sein: mit allen nur erdenklichen Mitteln (vgl. z.B. "mathematische Geschichten") ist eine innermathematische Anschaulichkeit zu vermitteln, und die zentralen Erkenntnisse sollten zu echter Anschauung geführt werden.

Z.B. müssen Tangenten (und überhaupt Lösungen) nicht nur berechnet, sondern vorweg "gesehen" werden (jede Aufgabenberechnung sollte anfangen: "was kann da denn eigentlich rauskommen?"). Im besten Fall bestätigt die Rechnung dann nur die vorher gesehene Anschauung oder macht die Ergebnisse genauer:

1. Anschauung: die Steigung der Tangente ist garantiert positiv und ungefähr 0,5 (aber garantiert nicht 10 000);

2. Rechnung: die Steigung der Tangente ist tatsächlich positiv (wenn Negatives rauskäme, wüßte ich durch die Anschauung vorweg, daß ich mich wohl verrechnet habe); und sie ist

1. tatsächlich exakt und nicht bloß ungefähr 0,5; oder sie ist

2. exakt 0,51, also in der Tat nah am vorhergesehenen Schätzwert.

(Ich lasse hier mal bewußt jene anderen Beispiele weg, bei denen die Anschauung einen nunmal täuschen kann bzw. überhaupt erst die Rechnung zu einem erstaunlichen Ergebnis führt. Im letzteren Fall wäre allerdings wieder zurückzuschalten:

1. hätte man das nicht doch vorher sehen können [und dann müssen wir beim nächsten Mal halt besser aufpassen];

2. wo im Laufe der Rechnung kommt das erstaunliche Ergebnis zustande?

Mathematik müßte also viel mehr nach dem wissenschaftlichen Verfahren "Hypothese → Experiment [= Rechnung] → bestätigte oder korrigierte Hypothese" verlaufen.)

Um "wirklich verstehen" zum Anspruch an Unterricht zu machen, muß auch der Lehrer sich immer wieder fragen, ob er denn selbst wirklich verstanden oder nur auswendig gelernt hat, ob ihm also alles nur zur (schnell zu verunsichernden) Gewohnheit geworden ist.

Ein bewußt simples Beispiel: ist Lehrern denn noch selbst gegenwärtig, wie wunderbar banal das Assoziativgesetz ist, und können sie es dementsprechend in die Alltagswirklichkeit von Schülern einbinden?

Es besagt doch nur eins: schon bei sowas erschütternd Simplem wie der Addition dreier Zahlen a, b und c strecken selbst die besten Mathematiker alle Viere von sich: keiner kann diese drei Zahlen "in einem Abwasch" addieren, sondern man addiert immer erst nur zwei Zahlen (z.B. a + b) und dann zum Ergebnis (e = a + b) die dritte (also e + c; d.h. wieder nur zwei Zahlen).

Glücklicherweise – und dafür sei den Göttern ewig Dank, denn sonst wäre die Mathematik von Anbeginn an extrem schwierig! – ist es aber schnuppe, welche zwei der drei Zahlen man als erste addiert: (a + b) + c = a + (b + c).

Aber so sehr "wirklich verstehen" Anspruch an jeden Unterricht sein sollte, ist er wohl naturgemäß nicht andauernd erfüllbar, sondern nur

1. immer mal wieder; d.h. auch: der eine Schüler versteht hier was, der andere da;

2. in einem langwierigen Prozeß, den zu begleiten, ja, auszuhalten der Lehrer geradezu bezahlt wird (um hier erst gar nicht von den Problemen der SchülerInnen zu reden):

für jedeN EinzelschülerIn wie für jede neue SchülerInnengeneration setzt sich (mathematische) Welt immer erst langsam zusammen, was auch heißt: "die Jugend von heute war noch nie so begriffsstutzig wie schon immer".

Das beste Beispiel (für mich selbst) bin ich da selbst: es hat ein ganzes Mathestudium gedauert (das mit Schulstoff nie was zu tun hatte, aber – auch durch Widerstand -mathematisches Denken hervorgebracht hat), bis mir im Nachhinein vieler Schulstoff ganz anschaulich erschien.

Und doch setzt sich auch für mich selbst heute und wohl auch in Zukunft vieles erst nach und nach zusammen. Ich habe pars pro toto lange gebraucht, um zu bemerken: der Logarithmus ist im Grunde genau dasselbe wie die Wurzel, nämlich herrlich genial um die Ecke gedacht.

"Wirklich verstehen" heißt für mich insbesondere, "mathematische Denkweisen" und strukturelles Denken (eben z.B. die Ähnlichkeit der Wurzel- und Logarithmusdefinition) beizubringen. Woraus z.B. folgt: fachfremder Mathe-Unterricht in der Unterstufe aufgrund Lehrermangels

(daß also beispielsweise ein Erdkundelehrer Mathe unterrichtet [denn Bruchrechnung kann ja angeblich jeder], wie an einer mir bekannten Schule inzwischen üblich)

ist schlichtweg unverantwortlich

(genauso würde man mit einem umgekehrt fachfremd in Erdkunde eingesetzten Mathe-Lehrer den Bock zum Gärtner machen).

Die Alternative zu "wirklichem Verstehen" ist aber "Fast richtig um die Ecke gedacht".

Zentral mit der Frage, inwieweit SchülerInnen "wirklich verstehen" und es lernen können, hängt zusammen, inwieweit wiederum die LehrerInnen ihre SchülerInnen in ihrem Nicht-Verstehen verstehen können. Kann ein Lehrer, der sich das Unverständnis (oder vielleicht nur ein anderes Verständnis) nicht mehr vorstellen kann, überhaupt vom Unverständnis zum Verständnis führen? Bestehen zwischen ihm und dem Schüler überhaupt noch Brücken, oder setzt er immer schon Verständnis voraus - und wundert sich dann, daß keins da ist?

Verständnis (oder um mit Rudolf vom Hofe zu sprechen: "Grundvorstellungen mathematischer Inhalte") ergibt sich vielleicht durch lange Arbeit und Gewöhnung. Mag sein, daß ein spontaner Heureka-Effekt hinzukommt. Manchmal scheint mir aber eher: wenn man dann verstanden hat und sich über dieses neue, sich nebenher eingestellt habende Verständnis fast wundert und gar nicht mehr recht weiß, wann es sich ergeben hat (nämlich in einem langen Prozeß der Gewöhnung, nicht aber in einem spontanen Augenblick), konstruiert man sich erst im Nachhinein einen mythischen Heureka-Effekt oder "Musenkuß": über Gewöhnung bzw. Prozesse läßt sich schwer reden, sie lassen sich nicht fassen, also braucht man einen Augenblick.

Vielleicht gab es auch in der "großen" Wissenschaft sehr viel mehr unmerkliche Evolutionen als REvolutionen, und erst im Nachhinein hat man aus den Evolutionen REvolutionen stilisiert?!

Auf jeden Fall "hat" man dann irgendwann das Verständnis - und kann nicht mehr ganz hinter es zurück: man hat den verschwommen verständnislosen Menschen, der man selbst mal war, vergessen, man ist ein neuer geworden. Es ist wie mit Kippfiguren:

Erst sieht man darin vielleicht (rechts und links, schwarz) zwei sich anschauende Gesichter im Profil. Und plötzlich "kippt" das Bild, und man sieht einen Pokal oder Kelch (in der Mitte, weiß). Oder eben umgekehrt.

Bezeichnend an solchen Kippfiguren ist aber eben, daß die Anschauung vom einen auf den anderen Augenblick kippt und man nachher kaum mehr das sehen kann, was man vorher noch gesehen hat. Analog: vorher sieht hat man nur Unverständnis, nachher nur Verständnis - und kann sich gar nicht mehr sein Unverständnis vorher vorstellen und kaum in es zurückspringen.

Ein Beispiel: ich glaube tatsächlich, daß, wer erstmal die Wurzel verstanden hat

(das EINZIG Wichtige und Interessante an der Wurzel aus 2 ist, daß ihr Quadrat wieder exakt 2 ergibt; aber ihr popeliger Dezimalwert [das, was jeder blödsinnige Taschenrechner anzeigt], also 1.4142135623731..., ist doch völlig uninteressant und konfus, weil irrational),

kann nie wieder ganz dahinter zurück.

Die Schwierigkeit, nicht mehr hinter sein Verständnis zurückspringen zu können, gilt es (und genau darum geht´s mir hier!) anzuerkennen: wenn ein Lehrer mal zu mir sagte, er könne sich "selbstverständlich" die Verständnisschwierigkeiten der SchülerInnen vorstellen, weil er sich an seine eigenen früher erinnere, so bin ich grundskeptisch (zumal gerade dieser Lehrer bei seinen SchülerInneN im Ruf steht, bei aller persönlichen Liebenswürdigkeit (und die ist grenzenlos wichtig!) doch meilenweit über aller (fachlichen) SchülerInnenwirklichkeit zu schweben.

Sich die Schwierigkeiten einzugestehen, SchülerInnenschwierigkeiten zu verstehen, heißt ja nicht, diese Schwierigkeiten nun gar nicht mehr zu verstehen:

• einerseits wird man ja sehr wohl einige Erinnerungen an eigene frühere Verständnisschwierigkeiten (und an Verzweiflung darüber!) haben;
• und andererseits kann man ja (immer ein gutes Rezept!) in Analogien denken:

"so, wie die SchülerInnen Schwierigkeiten haben, die Wurzel zu verstehen, habe ich (heute noch) Schwierigkeiten, die Quantentheorie zu verstehen: ich finde sie nur konfus, irritierend und gehirnausrenkend; und vor allem: ALLES ist mir unklar - bzw. ich meine sie zu verstehen, aber ich meine es wohl nur".

(Denn das ist ja auch wieder ein bekannter Effekt:

• die fälschliche Meinung vieler SchülerInnen, schon "alles" verstanden zu haben, und daraus fast notwendig folgend mangelnde Bereitschaft, noch mehr bzw. überhaupt zu verstehen;

• bzw. die glatte Unfähigkeit, Fehler zu sehen bzw. zu suchen.)

Schon gar nicht ist das Eingeständnis, oftmals die Verständnisschwierigkeiten der SchülerInnen beim besten Willen nicht verstehen zu können, mit der schlichten Weigerung, es doch immerhin zu versuchen, zu verwechseln. Ich werde solche im Lehrerberuf durchaus vorkommende Weigerung nicht gutheißen, kann sie aber doch immerhin verstehen:

• am wenigsten noch bei jungen LehrerInneN, die offensichtlich von Anfang an kein Verständnis für Jugendliche haben, die keine Menschen (SchülerInnen) lieben können (was man früher so "pädagogischen Eros" nannte) - und die   niemals selbst jung waren. Es gibt tatsächlich - und für mich doch grenzenlos erstaunlich! - merkwürdige Menschen, die "erwachsen" auf die Welt kommen!
• eher schon nach langer Dienstzeit aus Resignation oder gar Selbstschutz; oder genauer: aus einer Empfindlichkeit, die nur verzweifelt in Härte und Ablehnung umgedreht wird. Z.B. halte ich folgenden Effekt doch immerhin für verständlich:

"jetzt bringe ich »denen« schon seit 30 Jahren den Satz des Pythagoras bei, und diese Hornochsen verstehen ihn noch immer nicht".

Der Irrtum besteht natürlich schlicht darin, daß es nicht immer dieselben, sondern neue "Hornochsen" waren; und er besteht darin, vergessen zu haben, daß es im Lehrerberuf in allererster Linie um ganz individuelle (immer gänzlich neue) Menschen und erst in zweiter Linie um das Fach geht, ja, daß das Fach nur Mittel zum Zweck (der "Erziehung" und "Bildung") ist.

Das Beispiel der Kippfigur hilft (nicht nur in diesem [mathematischen bzw. pädagogischen) Fall weiter:

1. kann die Figur (ab und zu) zurückkippen: plötzlich sieht man wieder die Gesichter und nicht den Pokal/Kelch;
2. man kann es tatsächlich schaffen, beides zu sehen, also sowohl die Gesichter als auch den Pokal/Kelch:

Das sind zwei Gesichter, die zwischen sich einen Pokal/Kelch gestellt haben:

nunja, eine ziemlich blödsinnige Aktion (wieso und zu welchem Zwecke sollte man einen Pokal/Kelch zwischen sich stellen!???); aber immerhin gibt es da ein genauso blödsinniges und dennoch verständnisförderndes äquivalent: dieses saublöde und doch allemal "erotische" Partyspiel, bei dem zwei Partner mit einer Apfelsine zwischen den Stirnen miteinander tanzen müssen, und das Paar, dem das am längsten gelingt, hat gewonnen.

Beides zu sehen, also sowohl die Gesichter als auch den Kelch/Pokal, ist schlichtweg die utopische und manchmal dennoch stattfindende hegelsche Synthese (beides zu sehen) aus These (Gesichter) und Antithese (Pokal/Kelch).

(Das Wichtigste ist nebenbei das Wort "auch".)

Um aufs (nicht nur mathematische bzw. pädagogische) Problem zurückzukommen: man kann beides verstehen: das Verstehen und die Verständnislosigkeit. Aber man kann es erst, wenn man sich die Schwierigkeit, die Verständnislosigkeit zu verstehen, eingesteht.

Kleiner und letzter Exkurs

(der weit über die Mathematik hinausgeht, weil Mathematik nur ein [wunderschöner!] Teil des manchmal überquellenden, manchmal verzweifelten Lebens ist):

das (beides zu denken) paßt leider in so entsetzlich wenige Gehirne. Nehmen wir nur mal das Beispiel "Jürgen von der Lippe": weil er mal einen einzigen kirchenkritischen Satz gesagt hat, hat ihm irgendso eine katholische Zeitschrift angepißt, er hasse geradezu verbiestert die Kirche. Seine simple Reaktion, als man ihm dieses Zitat vorhielt: "glatt im Gegenteil!" Dieses "glatt im Gegenteil" beweist wahre Intelligenz

(und werden sowohl die Billig-Katholiken als auch die [sowieso] Billig-Atheisten nie verstehen, weil ihre Gehirnleistung dazu einfach nicht ausreicht!).

PS: Einzig wichtige, ja, zentrale Frage an neue "pädagogische" Trends (z.B. Internet in Schulen, Computer-Algebra-Systeme im Mathematik-Unterricht) ist: inwieweit ermöglichen sie es (schaffen sie Zeit und Muße), Denkweisen zu erfahren - oder lenken sie nur davon ab? Bzw. wie müssen solche Trends gestaltet werden, damit sie die Erfahrung von Denkweisen befördern?

D.h. beispielsweise für den Einsatz des Internets in Schulen: mit der Bereitstellung der technischen Möglichkeiten ist kaum erst der Anfang getan, es muß noch langwierig ein ausgefeiltes pädgogisches Konzept entwickelt werden. Denn "Surfen" ist noch lange keine Pädagogik, ein "Hyperlink" noch lange kein Verständnis.