wozu ?

vgl. Dieser Aufsatz ist durchaus exemplarisch gemeint, d.h. er geht über die Erarbeitung von π und überhaupt die Geometrie hinaus und betrifft vor allem , wie sie sich auch z.B. bei der Herleitung irrationaler Zahlen anhand der zeigen. Vgl. . Und auch methodisch ist dieser Aufsatz, wie man am Ende sehen wird, exemplarisch gemeint.

Wozu man  im "richtigen" Leben braucht? Kommt drauf an, wer "man" ist:

1. Der Durchschnittsbürger braucht es nie!
2. Ein Techniker muss wohl die Formeln

• U = 2 r   für den Kreisumfang
• F =    r² für die Kreisfläche

wenn schon nicht auswendig kennen, so doch in einer Formelsammlung nachschlagen und dann anwenden können. Und ebenso muss er  ≈ 3,14 kennen und evtl. genauere Werte vom Taschenrechner ablesen können.

Selbst der Techniker braucht also nur 2 ¹/₂ auswendig gelernte Formeln, die man ihm in 2 ¹/₂ Minuten verklickern kann.

Ausnahmslos alles, was im Unterricht meist der 10. Klasse zum Thema veranstaltet wird, ist also im Hinblick auf jegliche Anwendung überflüssig.

Das Beste, was man - so gesehen - über noch sagen, bzw. das Einzige, was ein Laie vielleicht nachvollziehen kann, ist, dass der Buchstabe (nicht der Zahlenwert) einen gewissen ästhetischen Reiz hat:

(Nachdem das gesagt ist, kann ich ab sofort den leichter handhabbaren, wenn auch nicht annähernd mehr so schön geschwungenen Computerschriftbuchstaben π verwenden.)

Nur kurz erwähnt sei ein anderes Problem mit π : es ist nicht nur "irrational"

(womit sich mitten in der Mathematik eine herrliche Unvernunft andeutet),

sondern sogar hübsch metaphysisch "transzendent":

• "irrational" bedeutet, dass π die in der Dezimalschreibweise hinter dem Komma weder endlich noch periodisch ist:

π = 3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 und in alle Ewigkeit auf unregelmäßige Weise weiter

π ist also unter keinen Umständen vollständig aufschreibbar.

... womit sich doch die dringliche Frage stellt, was man von solcher Erkenntnis "hat": macht das nicht jegliche Beschäftigung mit dem genauen Wert von π aussichtslos und somit überflüssig? Reichen nicht z.B. die ersten fünf Nachkommastellen, also π ≈ 3,14159?

Und weil π irrational ist, gibt es für das vollständige π mit seinen unendlich vielen, unregelmäßigen Nachkommastellen - ähnlich wie für die ebenfalls irrationale Zahl - prinzipiell keinerlei Anwendbarkeit! Selbst die besten Computer der Welt können nicht anders, als die Dezimalschreibweise von π irgendwann (evtl. nach abermillionen Nachkommastellen) abzuhacken, also mit - evtl. allerdings sehr genauen - endlichen Näherungswerten zu rechnen. Wen aber stört solch minimale Ungenauigkeit? Wirkt da das Bestehen auf dem exakten, wenn auch irrationalen Wert nicht weltfremd bzw. besserwisserisch?

Die Irrationalität von π wird im Schulunterricht zwar oftmals genannt, aber nie bewiesen

(was viel zu schwierig wäre).

Aber immerhin wird sie durch das "Einschachtelungsverfahren" (s.u.) nahegelegt.

• Im üblichen Unterricht nicht mal genannt wird hingegen die Transzendentalität von π, geschweige dass sie bewiesen würde

(der Beweis wäre zumindest für SchülerInnen/Laien vollends unverständlich).

Das Problem steckt natürlich im Wörtchen "nur":

1. ist die "andere, innermathematische Ebene" vielleicht nur bereits (von Geburt an?) mathematisch denkenden Geistern zugänglich - und anderen auf ewig verschlossen?
2. lässt sich die "andere Ebene" vielleicht gar nicht überzeugend bzw. verständlich an SchülerInnen/Laien vermitteln, und wenn doch, wäre zu fragen,
3. wie das geschehen könnte.

Ein mir vorliegender Unterrichtsentwurf sieht (abgekürzt) folgendermaßen aus:

1. ist die "Kreisverhältniszahl" π den SchülerInnen bereits bekannt

(vermutlich wurde vorher hergeleitet, dass π mittels der Formel U = 2 π r oder vielleicht auch F = π r2 den Kreisumfang U mit dem Radius bzw. die Kreisfläche F mit dem Radius in Verbindung bringt bzw. dass mit diesen Formeln der Umfang U bzw. die Fläche F aus dem Radius berechnet werden kann;
der Zahlenwert π ≈ 3,14159 muss dabei ja noch nicht bekannt sein, sondern soll vermutlich in der vorliegenden Unterrichtseinheit gesucht werden).

2. werden den SchülerInnen die ersten Schritte des archimedischen Annäherungsverfahrens für π

(vgl. und dort "Geometrie" - "Kreisfläche/-Umfang")

gezeigt und wird dann sozusagen ex cathedra mitgeteilt, dass Archimedes damit die Annäherung gefunden hat.

3. werden die SchülerInnen aufgefordert, das archimedische Annäherungsverfahren (u.a. mit Hilfe einer Geometriesoftware) weiterzuführen und dadurch genauere Werte als Archimedes zu finden.

Für meinen Geschmack hat solch ein Unterrichtsentwurf entscheidende Nachteile:

1. wird mit 1. Entscheidendes vorausgesetzt bzw. ausgeblendet: wie kommt man denn überhaupt erst auf die "Kreisverhältniszahl" π, aber auch: wieso (wozu) sucht man denn überhaupt nach ihr?
2. wird das archimedische Verfahren bereits verraten, statt dass die SchülerInnen es (ansatzweise) selbst finden können.
   Die ausdrücklich als "Selbstlern-Einheit" verstandene Unterrichtseinheit drückt sich also um das Selbstentdecken bzw. hält es a priori für ausgeschlossen

(vermutlich mit dem allemal guten Grund, dass es [tatsächlich oder angeblich] eine Überforderung der SchülerInnen wäre, dass sie selbst auf die Erkenntnisse eines der genialsten Mathematikers der Weltgeschichte kommen sollen). 

Das "Selbstlernen" bezieht sich in der vorliegenden Unterrichtseinheit also "nur" auf die Art und Weise, wie vorgegebene Schritte durchgeführt werden (Gruppenarbeit, gegenseitige Hilfe, Präsentation ...).

In der Tat ist das selbstentdeckende Lernen ja eine heikle Sache, aber doch nicht völlig ausgeschlossen. Vgl. . Oftmals scheitert es aber schlichtweg daran, dass die SchülerInnen es "von Natur aus" (???) nicht wollen oder es ihnen abgewöhnt wurde. Ein Grund dafür ist, dass die Mathematik immer als Betonklotz erscheint, der fertig vom Himmel fällt und an dem es nichts mehr zu tun gibt bzw. den man nur noch (mühsam) nachvollziehen kann.

Konkret: viele SchülerInnen wissen schon vor der entsprechenden Unterrichtseinheit, dass es eine Zahl π ≈ 3,14 gibt, und verweisen auch darauf, dass im Mathebuch genauere Werte von π sowie die fertigen Formeln für den Kreisumfang und die Kreisfläche stehen. Was also, außer sie nachzuvollziehen, gibt es noch zu tun?

3. wird die höchst interessante (s.u.) archimedische Annäherung anscheinend nur nebenbei

(als gegeben und "nur" zu verbessern)

 genannt, statt genauer untersucht und als Erkenntnismöglichkeit genutzt zu werden.

Zu a.,

also der Frage, wie man denn überhaupt auf die Kreisverhältniszahl π kommt bzw. wozu man sie sucht

(weshalb man sie überhaupt suchen will?).

Es ist sogar noch vertrackter: anfangs sucht man wohl noch gar nicht nach π, sondern man findet es erst nach einigen Überlegungen - und stellt dann fest, dass es höchst merkwürdige (unangenehme?) Eigenschaften hat.

*

Man wird wohl kaum um eine (gar nicht so selbstverständliche?) Voraussetzung herumkommen, nämlich dass man den Kreisumfang bzw. die Kreisfläche herausfinden will.

(Wir werden noch sehen, das für den Laien "herausfinden" wohl eher "nachmessen" als "rechnen" bedeutet.)

Und eine weitere nötige Voraussetzung ist wohl die Überlegung, dass der Kreisumfang U und die Kreisfläche F "irgendwie" vom Radius r bzw. Durchmesser d abhängen: wenn r bzw. d größer/kleiner wird, werden auch U und F größer/kleiner.

Das Problem dabei ist natürlich das "irgendwie": wie denn genau

(falls sich das überhaupt herausfinden lässt)?

*

Üblicherweise fängt man da beim Kreisumfang an, und zwar vermutlich, weil dieser Versuch auf die einfachere (lineare, also nichtquadratische) Gleichung U = 2 π r hinausläuft.

Und dennoch ist dieser Einstieg mit dem Kreisumfang doppelt zweifelhaft:

• Es gibt auf Anhieb keine Notwendigkeit, mit dem Radius r zu arbeiten, sondern genauso gut könnte man mit dem Durchmesser d arbeiten, womit sich ergäbe: U = π d.

Später, bei der Kreisfläche, ergäbe sich damit die Formel F = π (^d/₂)² = ¹/₄ π d², was den Nachteil hätte, dass man für ¹/₄ π einen Zahlenwert von ungefähr   0,78539 erhielte, an dem die Verwandtschaft mit π ≈ 3,14159 (dass es ein Viertel davon ist) nur schwerlich zu erkennen wäre.

Umgekehrt hat U = π d natürlich den Vorteil, dass man da in der Tat π ≈ 3,14159 herausbekommt, während man bei U = 2 π r für 2 π ungefähr  6,28318 herausbekommt, woran wiederum kaum die Verwandtschaft mit π ≈ 3,14159 (dass es das Doppelte ist) erkennbar ist

(solche Überlegungen sind aber für Durchschnittsschüler wohl viel zu schwierig):

wie man´s macht, macht man´s verkehrt.

Nun hat sich aber der Umgang mit r und nicht mit d eingebürgert - was doch immerhin zu motivieren wäre:

• man hat also die Wahl zwischen
  • einerseits     U =    π d und F = ¹/₄ π d²,
  • andererseits U = 2 π r und F =       π r²

^{(das weiß man aber erst, wenn man - was im Unterricht allerdings kaum üblich ist - sowohl den Kreisumfang als auch schon die Kreisfläche hergeleitet hat).}

Da ist einem Mathematiker ¹/₄ (eine Division) doch viel zu schwierig und daher die zweite Möglichkeit , also U = 2 π r und F = π r², lieber.

• Im "Alltagsleben" tauchen Kreise immer fertig auf, d.h. wohl die Kreislinie, aber weder Mittelpunkt noch der Durchmesser d oder der Radius r. Da der Mittelpunkt aber nachträglich gar nicht so einfach zu finden ist, wird ein Laie

(wozu es allerdings, wie gezeigt, keinerlei "lebensweltliche" Notwendigkeit gibt)

vermutlich höchstens

(und wohl nur ungenau, da auch die Durchmesserkonstruktion ganz schön schwierig ist)

den Durchmesser d ("so ungefähr")

,

aber nicht den Radius r ausmessen

(der natürlich schnell durch Halbierung von d erhältlich wäre, wofür es aber gar keine Notwendigkeit gibt).

Stattdessen dennoch vom Radius r auszugehen, ist schon erheblich mathematisch gedacht: der Kreis ist mathematisch überhaupt erst durch seinen Mittelpunkt und seinen Radius (!) definiert: alle Punkte der Kreislinie liegen im (gleichen) Abstand r vom Mittelpunkt, bzw. wenn ich einen Kreis zeichnen will, trage ich mit einem Zirkel um den zuerst gezeichneten Mittelpunkt eine Linie mit dem Radius r ab.

Anders gesagt: es gibt mathematisch gar keine fertigen Kreise, sondern sie werden erst durch Konstruktion hergestellt.

• Wenn ein Laie (einE SchülerIn) den Kreisumfang herleiten soll, wird sie/er vermutlich das schlichtweg Naheliegende tun, nämlich ein biegbares Metermaß, also beispielsweise ein

 
Schneidermaßband,

um den Kreis herum legen und dann den Wert für den Umfang (ohne jede Rechnung!) ablesen

(nebenbei: papierene Maßbänder in Klassensatzstärke kann man am besten bei IKEA bekommen).

Bei einem Kreis mit dem Radius r = 10 cm erhält unser Laie also einen Umfang von (ca.)  62,8 cm

(da die Millimeter die kleinste auf dem Maßband vorhandene Maßeinheit sind).

Wenn die Formel U = ? ∙ r schon als wünschenswert hergeleitet ist, erhält er also

    62,8 cm = ? ∙ 10 cm  | : 10 cm

       6,28       = ?

(Wohlgemerkt: hier tritt, wie oben bereits gezeigt, das Problem auf, dass sich nicht ein Näherungswert für π, sondern für sein Doppeltes ergibt, an dem das π kaum erkennbar ist.)

Nun kann man den linearen  Zusammenhang U = ? ∙ r "eigentlich" nicht aus einem einzigen Beispiel folgern (da funktioniert solch ein linearer Zusammenhang immer) - was allerdings für Laien/SchülerInnen wohl kaum ein Argument sein wird: für sie ist nach einem Beispiel vermutlich "alles" klar - und kein weiteres Beispiel nötig bzw. jedes weitere zu umständlich.

Allemal hat aber der lineare Zusammenhang U = ? ∙ r den Vorteil, dass er erheblich leichter zu erkennen ist als der quadratische Zusammenhang bei F = ? ∙ r², und genau das ist wohl der Grund, weshalb man trotz der bereits gezeigten Nachteile der Umfangsberechnung im Unterricht üblicherweise dennoch mit dieser beginnt.

Oben war gesagt worden, man erhalte bei einem Kreis mit dem Radius r = 10 cm einen Umfang von (ca.) 62,8 cm und somit ? = 6,28.

Das zentrale Problem ist da das kleine "ca.":

• Laien werden vermutlich gar nicht erkennen, dass 62,8 cm nur eine Näherung ist, denn die kleinstmögliche ablesbare, nämlich die Millimeterzahl, wurde ja "korrekt" abgelesen.

(Und Laien würden vermutlich selbst dann, wenn sie merken würden, dass es nur ein Näherungswert ist, einwenden, dass das doch wohl genau genug sei, also gar kein Interesse an der "Fliegenbeinzählerei" noch genauerer Werte haben.)

Laien werden Messungenauigkeiten also vermutlich gar nicht bemerken.

• ? = 6,28 hat sogar noch eine Nachkommastelle mehr, und wenn man da - was ja doch naheliegt - noch immer in Zentimetern und Millimetern denkt (obwohl die Zahl keine Maßeinheit mehr hat), ist man mit der zweiten Nachkommastelle wohl längst in einem Genauigkeitsbereich (Zehntelmillimeter) angelangt, der Laien vermutlich endgültig irrelevant erscheint.

Laien werden Messungenauigkeiten, wenn sie sie denn überhaupt sehen, also vermutlich herzhaft egal sein.

Vielleicht war aber schon die Vorgabe r = 10 cm ungünstig, weil bei ihr Messungenauigkeiten gar nicht erst klar werden oder unerheblich sind (erscheinen).

Vielleicht wäre es also doch günstiger, mit einem kleineren Kreis beispielsweise mit dem Radius r = 1 cm (dem "Einheitskreis") zu beginnen, bei dem Messungenauigkeiten eher auffallen, und zwar insbesondere, wenn mehrere SchülerInnen messen und (hoffentlich!) unterschiedliche Ergebnisse bekommen.

Und überhaupt sollte man die SchülerInnen den Umfang (die Umfänge?) verschieden großer Kreise

und daraus (unterschiedliche!) Näherungen für ? bzw. π herleiten lassen.

Schauen wir uns nun aber die Herleitung der Kreisfläche F = π r² an:

1. hat sie, wie schon gezeigt, den Vorteil, dass da für F = ? ∙ r² direkt ? = π und nicht ein Vielfaches oder ein Teil von π herauskommt, dass also das π direkt ablesbar ist.
2. aber hat die Herleitung der Kreisfläche den Nachteil, dass die Abhängigkeit von r quadratisch und somit wohl nicht so einfach erkennbar ist.

(Eine kleine Eselsbrücke kann da sein, dass Flächen in Quadratzentimetern bzw. cm² gemessen werden.)

3. scheint mir aber der entscheidende Vorteil der Kreisflächenberechnung zu sein, dass sie nicht mit einem Maßband "erschlagbar" ist, sondern man um eine Annäherung/Einschachtelung (und einfache Rechnungen oder zumindest Abzählen) einfach nicht herum kommt.

Es ist wohl naheliegend, dass man mangels Alternativen jegliche Flächenmessung mit "geraden" Maßen (Quadraten, Rechtecken) versuchen wird. Aber genau das sollte auch als entscheidende, weit über die Kreismessung hinaus, nämlich auch für die spätere Integration wichtige Erkenntnis herausgearbeitet werden:

: Mathematiker können überhaupt nicht mit "krummen" Figuren, sondern nur mit geraden (Dreiecken, Quadraten und Rechtecken) umgehen, machen aber aus dieser Not eine Tugend, indem sie krumme durch gerade Figuren annähern und auf diesem unvermeidlichen Umweg dann doch zu einer Lösung fürs Krumme kommen. Welche Erleichterung für SchülerInnen!: die Unfähigkeit, mit "krummen" Figuren umzugehen, beruht nicht darauf, dass die SchülerInnen (noch) "dumm" sind, sondern ist eine Art "Naturgesetz", mit dem auch die größten Mathematiker zu kämpfen hatten.

Ideal für die Kreisflächenberechung ist ein Millimeterpapier, das

• zusätzlich eine Zentimetereinteilung besitzt,
• auf durchsichtige Folie gedruckt ist, so dass die SchülerInnen es auf Kreise drauflegen und diese darunter sehen können:

Dabei lässt die Unterteilung sowohl in Zentimeter als auch in Millimeter die Frage offen, wie genau man denn messen möchte.

Weil der Kreis rund, alle Parkettierungselemente aber eckig sind, wird intuitiv deutlich, dass es niemals eine absolut passende Parkettierung geben wird - und seien die Pakettierungselemente noch so klein.

Angenommen aber mal, man möchte mit der Zentimeterrasterung anfangen. Dann kommt schnell die Frage auf, welche Parkettierung man denn überhaupt wählen möchte:

1. eine Parkettierung, deren Elemente ausschließlich innerhalb des Kreises liegen:

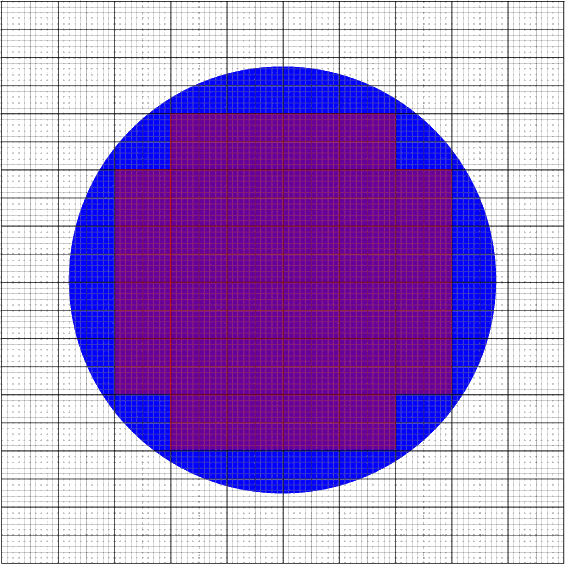
Diese Parkettierung ist offensichtlich zu klein!

2. oder eine Parkettierung, deren Elemente den Kreis völlig umfassen:

Diese Parkettierung ist offensichtlich zu groß!

In beiden Fällen wird aber die Anzahl der Quadratzentimeter abgezählt und dann eine Näherung für die Kreisfläche berechnet.

(Nebenbei: auch hier empfiehlt es sich, in der Klasse verschieden große Kreise ausmessen zu lassen, um

• die immer gleiche Abhängigkeit F = π r² von jedem Radius herzuleiten,
• aber auch zu verdeutlichen, dass die Messungen bei kleineren Kreisen [und anfangs vorgegebener Zentimeterunterteilung] ungenauer ist.)

Auch ohne das unterliegende Millimeterraster ist es naheliegend, dass man

• im Fall a. die Parkettierung verbessern kann, indem man feinere Einheiten (z.B. 0,5 cm ∙ 0,5 cm) hinzufügt:

• im Fall b. die Parkettierung verbessern kann, indem man feinere Einheiten (z.B. 0,5 cm ∙ 0,5 cm) abschneidet:

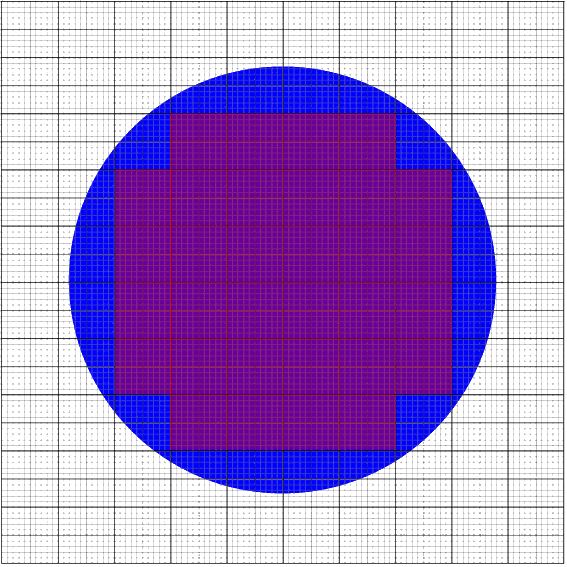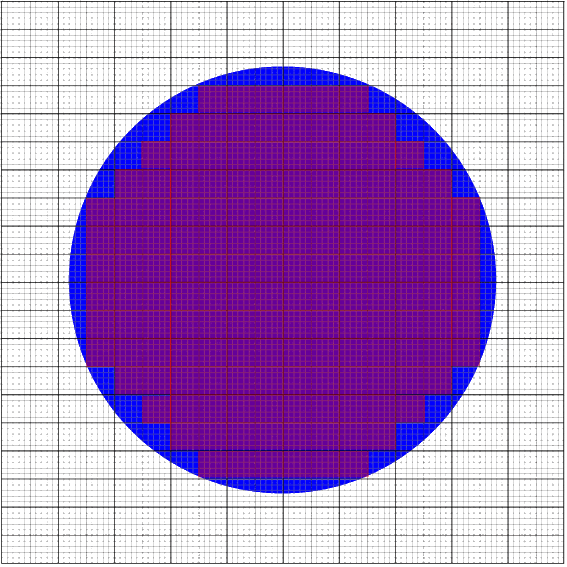
Im Grunde kann man damit schon aufhören, denn damit ist (auch im Hinblick auf ) Entscheidendes längst klar:

• Der reale Wert von F bzw. π ist - wie bereits gesagt - nur durch Annäherung (von außen bzw. innen) ermittelbar.

(Wohl wirklich zu kompliziert für SchülerInnen ist die [weitere] typisch mathematische Denkweise, dass es den "realen" Wert von π vorweg gar nicht gibt, sondern dass er überhaupt erst durch die Annäherung[en] zustande kommt.)

• Der reale Wert von F bzw. π liegt zwischen der Annäherung von außen und der von innen, womit die Einschachtelung naheliegt.
• Es erweist sich als sinnvoll, die Annäherungen systematisch durchzuführen, hier nämlich mit immer kleineren Quadraten

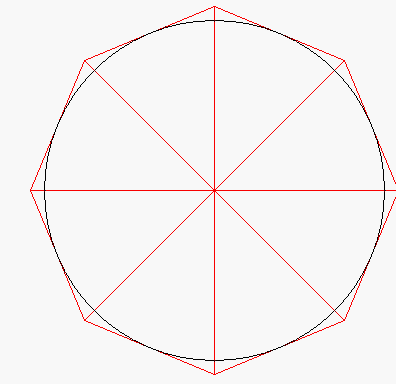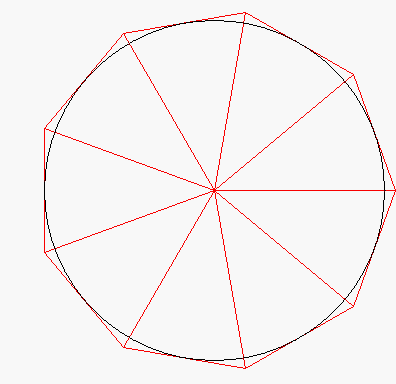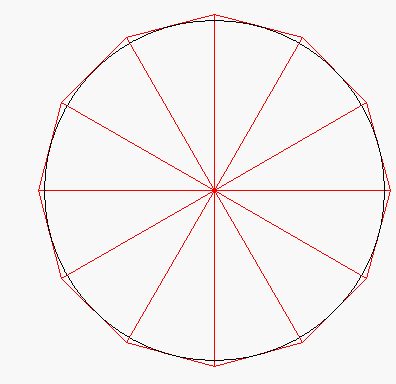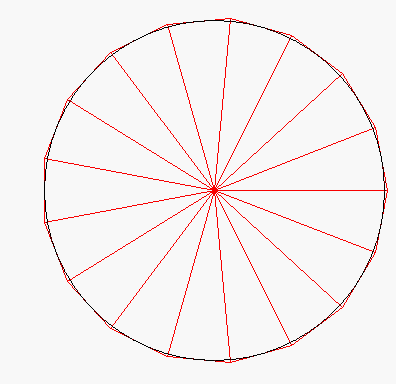
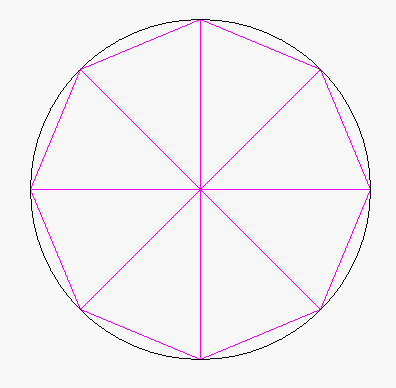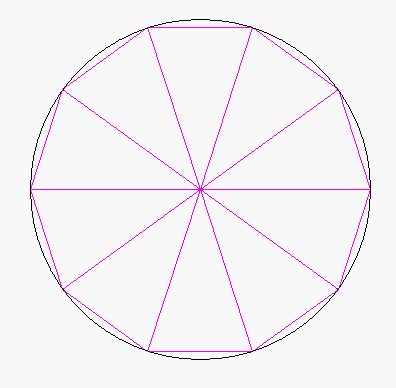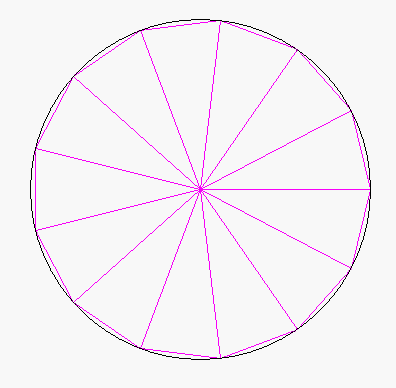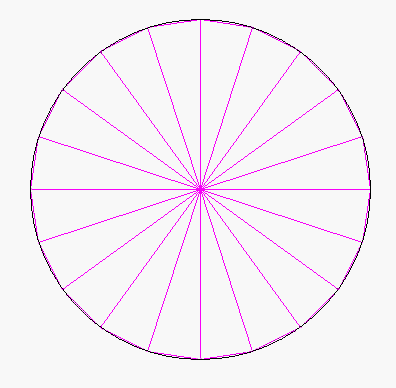
(... und dann braucht man den SchülerInnen nur noch mitzuteilen, dass Archimedes mit einer anderen sinnvollen Annäherung, nämlich über Vier-, Acht-, Sechzehn-...-Ecke, gearbeitet hat. Und da könnte man dann in der Tat überlegen, weshalb sich dadurch viele Rechnungen erheblich vereinfachen.)

Ich halte es also für wenig sinnvoll, die Verfeinerungen - was gar nicht so einfach und zudem bald wieder vergessen ist - von den SchülerInnen berechnen zu lassen, sondern das kann man doch nun, nachdem das Prinzip bzw. die mathematische Denkweise klar ist, getrost einem Computer überlassen. Z.B. bei einer nochmals anderen Außenannäherung des Einheitskreises, nämlich durch Dreiecke

(vgl. die Animation oben):

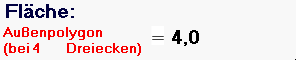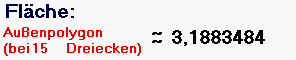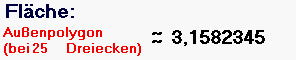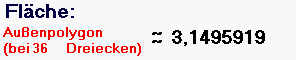
Ein anderer interessanter Einstieg könnte ein Detail aus dem oben genannten Unterrichtsentwurf sein, nämlich die Formel des Archimedes.

Zu allererst wäre mal kurz zu zeigen, dass (weshalb?) tatsächlich kleiner als und π somit wirklich eingeschachtelt ist.

Da stellt sich doch die Frage: warum eigentlich hat der immerhin doch bedeutende Mathematiker Archimedes nicht den exakten Wert von π angegeben, sondern nur eine Näherung?

Insgesamt wurde aber in meinen Überlegungen die Methodik (Selbstentdecken) aus dem konkreten Stoff hergeleitet, statt dass ihm nur allgemeine Methoden (Gruppenarbeit, Präsentation ...) übergestülpt wurden.

Das schließt ja nicht aus, dass man diese allgemeinen Methoden zusätzlich anwendet.

---

"Der Begriff Parallelwelt bezeichnet eine Welt, die gleichzeitig und parallel zur gewohnten Welt existiert. Parallelwelten sind vor allem aus der Science-Fiction bekannt, ihre theoretische Möglichkeit wird jedoch auch in der wissenschaftlichen Physik diskutiert. In einem übertragenen Sinne ist auch in der Psychologie von Parallelwelten die Rede." (Quelle: )

Der Sinn der Einführung von π ist ein rein innermathematischer: zu entdecken und zu erlernen, die später beispielsweise auch bei der Integration hilfreich sind. Das eben ist die oben genannte "andere Ebene".

Um daraus dennoch was fürs "richtige" Leben zu lernen, muss man es schon arg hinbiegen: in einigen Fällen kann nicht einmal die sonst so rechthaberische Mathematik die "Wahrheit" direkt erreichen, sondern nur annähern.

---

Als Dreingabe ein nettes Schmankerl zur Oberflächenbestimmung der Kugel: