die Grenzen der Veranschaulichung Mathematik in Bildern mathematische Denkweisen menschliche Mathematik Rechnen Funktionen Geometrie Wahrscheinlichkeit die leidige Alltagssprache Leipziger Allerlei

	"One of the saddest developments in school mathematics has been the downgrading of the visual for the formal." (Ian Stewart)
	"Ich hatte das Glück, auf Bücher zu treffen, die es nicht allzu genau nahmen mit der logischen Strenge [...]" (Albert Einstein)
	"Wenn Sie [...] bereit sind, einige human dargebotene Rechnungen nachzuvollziehen, dann sollten Sie auf jeden Fall weiterlesen!" (Gottfried Beyvers, Elvira Kusch)
	"Der Mensch ist ein Augentier, das stimmt, aber mit einem Gegenstand wirklich vertraut wird er doch erst, wenn er ihn in die Hand nehmen oder zumindest um ihn herumlaufen kann." (Ulf von Rauchhaupt)
	"An mehreren Stellen in diesem Buch habe ich mich unverfroren mathematischer Formeln bedient und damit die häufig ausgesprochene Warnung missachtet, dass jede solche Formel den Leserkreis halbieren wird." (Roger Penrose)
	"Für einen Wissenschaftler gibt es viele Gründe, ein populärwissenschaftliches Buch zu schreiben, und es gibt etliche Gründe, dies nicht zu tun. Das Primat jeder wissenschaftlichen Betätigung ist immer noch die Forschung: Hier werden Karrieren geschmiedet und Auszeichnungen verdient. Alles andere verbraucht demgegenüber nur kostbare Zeit - zumindest in den Augen mancher Kollegen, die vielleicht einmal zu einer Bewertung in einer wichtigen Entscheidung befragt werden. Doch was ist aller wissenschaftlicher Fortschritt wert, wenn man ihn nicht vermitteln kann? Verstehen wir die Welt wirklich, wenn wir sie nicht ohne die Voraussetzung eines langjährigen Studiums erklären können? Zu oft bedeutet das Erlernen einer komplexen Materie, dass man die entscheidenden Sachverhalte bloß akzeptiert und sich an eingespielte Rechenmethoden gewöhnt. Ein wahrer Test des Verständnisses wird erst erreicht, wenn dieses Wissen einem aufgeschlossenen, aber unvoreingenommenen Laien erklärt werden soll. In diesem Sinne ist z.B. die Quantenmechanik — trotz aller Erfolge und technologischer Anwendungen — keineswegs verstanden [...]. Ein populärwissenschaftliches Buch zu schreiben ist für einen Wissenschaftler also eine Übung, die auch für die eigene Forschung äußerst relevant ist." (Martin Bojowald)
	"Ein vollkommen aufgeklärtes (oder »reduziertes«) Problem ist langweilig [...]" (Mary Reppy)
	"Die erste Regel, an die man sich in der Mathematik halten muss, ist, exakt zu sein. Die zweite Regel ist, klar und deutlich zu sein und nach Möglichkeit einfach." (Lazare Nicolas Marguérite Carnot)
	"Alles sollte so einfach wie möglich gemacht werden, aber nicht einfacher." (Albert Einstein)
	"Wenn die Unterrichtsstunde [und schon die Unterrichtsvorbereitung] nicht damit endet, daß der Lehrer [keineswegs nur pädagogisch, sondern durchaus auch fachlich] etwas gelernt hat, weiß er nicht, wie man lehrt." (John Archibald Wheeler)
	"Nicht lehren, sondern vor-lernen."
	"Nie ist Wissenschaft anders entstanden als durch poetische Anschauung." (Ralph Waldo Emerson)
	Wer schon alles weiß, kann nur noch erklären, aber nicht mehr erzählen. (? )
	"Da wurde mir jahrelang beigebracht, mir nichts unter Mathematik vorzustellen, und nun soll ich plötzlich doch wieder eine Anschauung damit verbinden." (eine Schülerin)
	"Sind Formeln denn nicht nur rigide Denkkrücken oder Verständigungsformen für Mathematiker, die sich so ihre inneren Bilder gegenseitig mitteilen? Was ist Mathematik? Die Idee? Oder der Beweis? Die Formel? Oder das Bild?" (Gunter Dueck)

Mathematik in Bildern

Ausstellung





















 

mathematische Denkweisen

und


und 3^-5








und

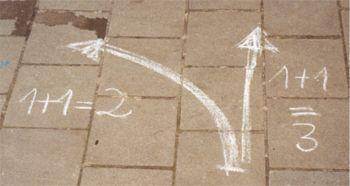Rechnen

Funktionen

:




und 




( Schülerversion)










↔

oder

     

die Welt ist

Geometrie

	AktienGesellschaft

 

     

Wahrscheinlichkeit

die leidige Alltagssprache

     

Mathematik