-Zuordnungen-Zuordnungen
| Es gibt verschiedene Arten der 3D-Projektion und damit auch der 3D-Brillen, darunter die PolfilterbrillenBei der farbigen Raumbildprojektion werden die beiden getrennten Bilder mittels polarisiertem Licht ausgestrahlt. [...] Die verschiedenen Bilder erreichen die Leinwand durch zwei verschiedene Projektoren bzw. Objektive. Jede der beiden Linsen wird dabei um einen Vorsatz mit entsprechend angeordneten Polarisationsfolien ergänzt. Die benötigte Brille besteht ebenfalls aus zwei Polarisationsfiltern, die bei den einzelnen Augen um 90 Grad gedreht sind und nur das „passend“ polarisierte Licht des entsprechenden Objektivs durchlassen, sodass wiederum jedes Auge nur „sein“ Bild erhält. [...] (Quelle: Die hier genannte Polarisation wird unten noch hilfreich sein. |
Natürlich gibt es gute Gründe, dass Großteile des üblichen Matheunterrichts sich mit Zweidimensionalem beschäftigen:
(wenn man - am Computer - nicht bewegliche 3D-Simulationen benutzt).
Deshalb kommt Dreidimensionales kaum im Schulunterricht vor, wenn man mal von den leidigen Körperuntersuchungen (Zylinder, Kegel ...) in der 10. Klasse und vektoriellen Gegenständen im Dreidimensionalen (Ebenen, Kugeln ...) absieht.
Das weitgehende Fehlen des Dreidimensionalen ist aber ganz grundsätzlich schade, weil alles Zweidimensionale zwar, wie etwa eine Parabel oder der Graph einer Sinusfunktion, auch seinen eigenen Reiz haben mag, aber letztlich doch - wie Strichmännchen - arg "abgenagt" ist.
Und "abgenagt" heißt eben auch "nicht be-greifbar".
Nehmen wir als Beispiel nur die Kugel, die in der zweidimensionalen Darstellung zum Kreis "verkommt". Und selbst das Bild einer Kugel ist nicht so "be-greifbar" wie eine echte, anfassbare Kugel
(die allerdings am besten poliert ist, um bei aller Materialität doch ihre Perfektion [also sozusagen die platonische Idee der Kugel] klar zu machen).
Und nebenbei: was ist eine pisselig kleine Kugel im Vergleich mit einer großen, massiven, schweren?:
Schon gar nicht kommen im üblichen Unterricht dreidimensionale Funktionen bzw. Zuordnungen vor.
Und genau das will ich hier mit zwei Ideen ändern:
1. ein Paraboloid
Fangen wir an mit der in Schulen weidlich ausgeschlachteten
Parabel.
... wobei man diese Parabel ja durchaus auch mal anfassbar machen kann
(am besten durch Hochglanz auch wieder die "Idee"):
Wir machen diese Parabel nun vollends dreidimensional, indem wir sie
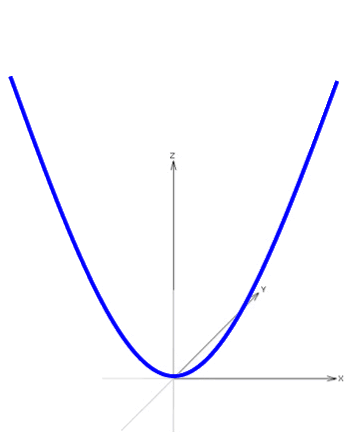
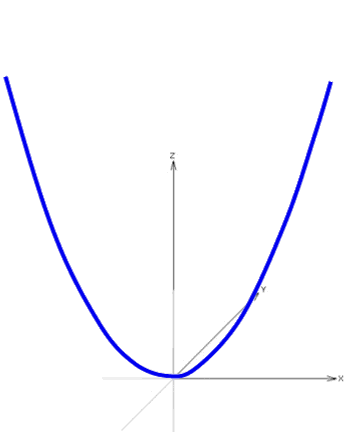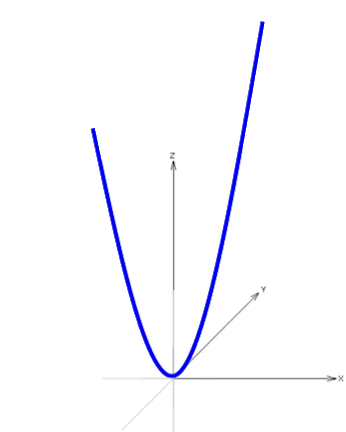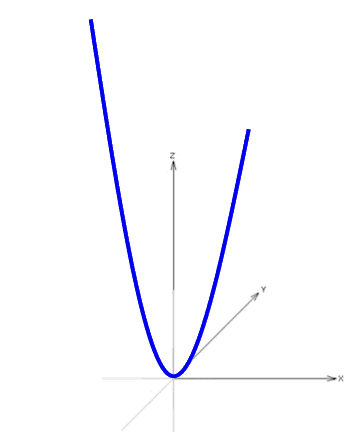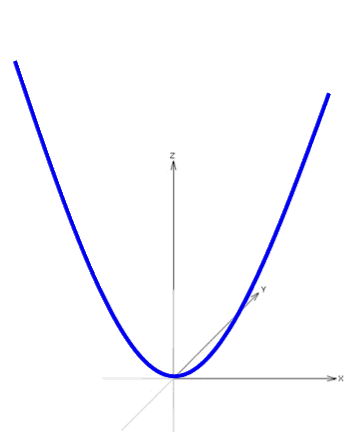
Alle nacheinander entstehenden Parabeln ergeben dann zusammen einen sogenannten (dreidimensionalen) Paraboloiden:
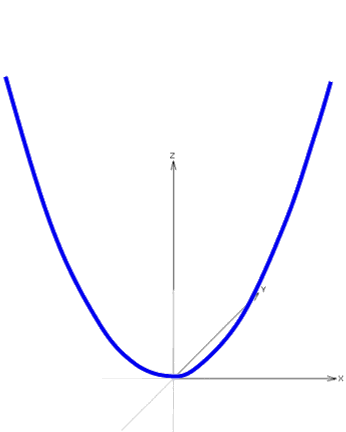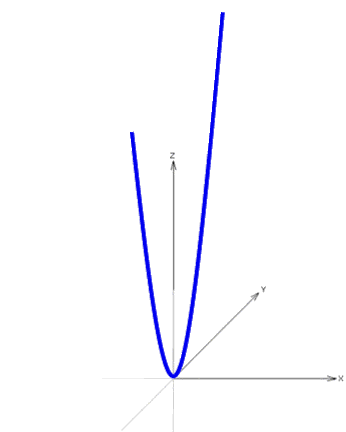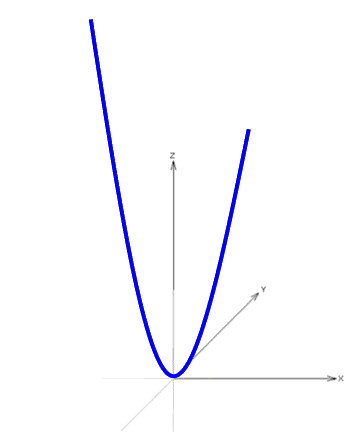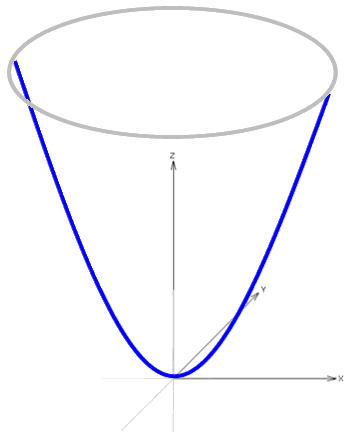
Oder besser doch wieder hübsch perfekt, also hochglänzend oder matt gebürstet:
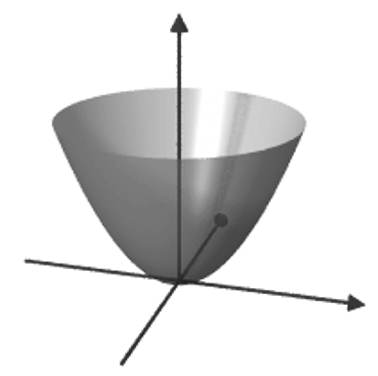
(Ein kleiner Exkurs zwischendurch: wir hatten den Paraboloiden durch Rotation einer Parabel erhalten, und genau da gibt es durchaus Anwendungsbeispiele, und zwar dann, wenn man einen Behälter mit einer Flüssigkeit darin rotieren lässt: die Flüssigkeit nimmt Paraboloidenform an
[... wobei hier nicht geklärt sei, warum das so ist]:
- allerdings mit dem Nachteil, dass man diese Rotationsspiegel nicht kippen, also nur das sehen kann, was direkt über ihnen ist;
)Nun kann man sich natürlich streiten, was man davon "hat", wenn man für einen schönen Paraboloiden auch noch die Funktionsgleichung aufstellen kann. Immerhin soviel: wer einen Paraboloiden herstellen oder auch nur mit dem Computer simulieren will, wird wohl die Funktionsgleichung des Paraboloiden kennen müssen.
Die Herleitung dieser Funktionsgleichung soll im Folgenden anhand eines einzigen, allerdings gleich allgemeinen Paraboloidenpunktes P mit den Raumkoordinaten x, y und z geschehen:
*
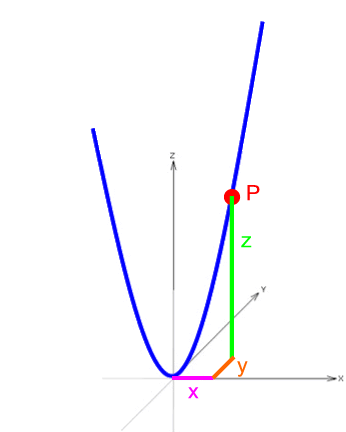
Hier sei gleich gefragt, wie denn die Koordinaten x, y und z des Punkts P zusammenhängen.
Dazu schalten wir zum ersten Mal einen Gang zurück zur altbekannten (zweidimensionalen) Parabel:
bei ihr kann x frei gewählt werden, wenn man es aber erstmal ausgewählt hat, ergibt sich y abhängig von diesem x automatisch:
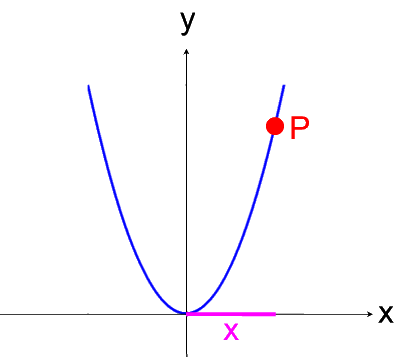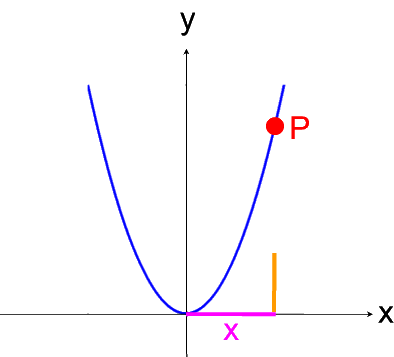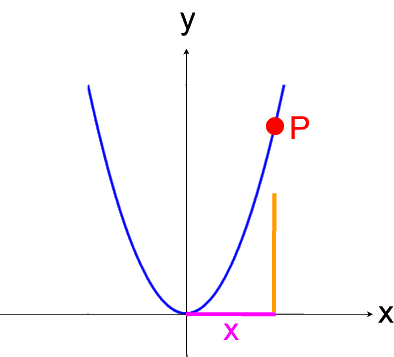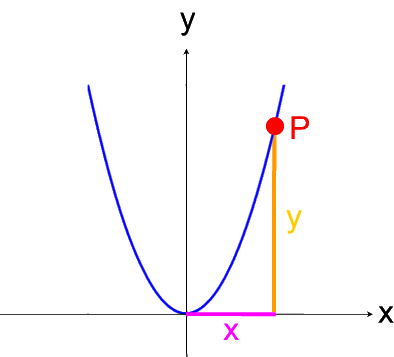
Diese Abhängigkeit des y vom vorher gewählten x drückt man üblicherweise durch eine Funktionsgleichung aus, mittels derer man das y aus dem x berechnen kann:
| y = irgendwas mit x |
Im Fall der (Normal-)Parabel:
| y = x2 |
Beim dreidimensionalen Paraboloiden gilt:
x und y können frei gewählt werden, wenn man sie aber erstmal ausgewählt hat, ergibt sich z abhängig von diesem x und y automatisch:
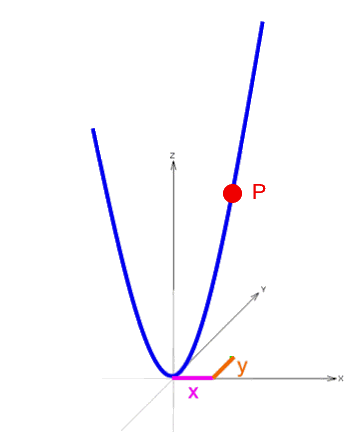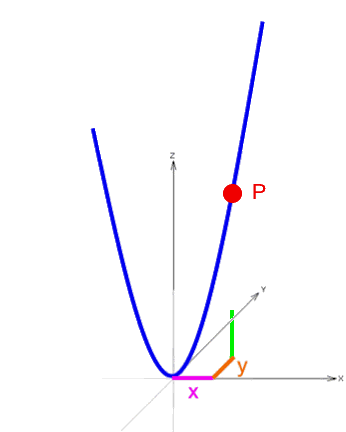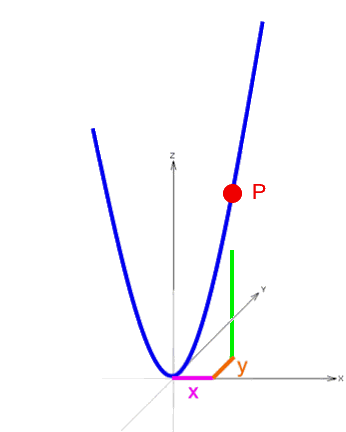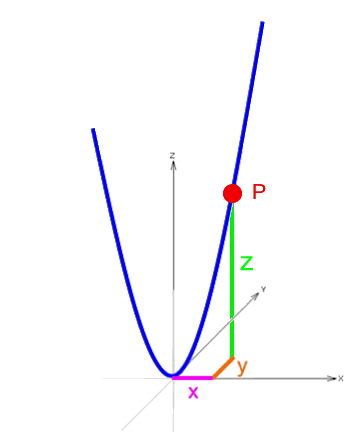
Wir suchen also eine Funktionsgleichung, in der z abhängig von x und y ist, d.h.
| z = irgendwas mit x und y |
Gerade durch die Erweiterung vom Zwei- zum Dreidimensionalen lernen wir also: es ist immer nur eine einzige Unbekannte abhängig
(bei der Parabel x, beim Paraboloiden z),
und zwar von allen anderen
(bei der Parabel von x, beim Paraboloiden von x und y).
*
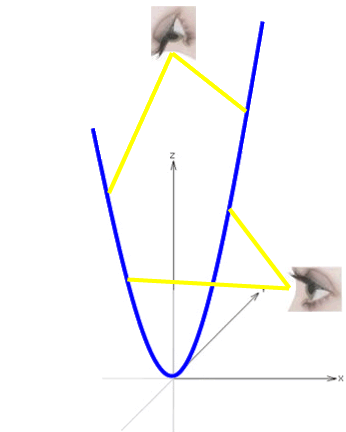
Überhaupt können "wir" mit der Zeichnung
schwer umgehen, weil die zweidimensionale Projektion doch sehr die Verhältnisse verzerrt, nämlich rechte (!) Winkel nicht als solche erscheinen.
Und es ist ja sowieso immer gut, sich klar zu machen, was man
und dann mit Letzterem auf Umwegen doch Ersteres anzugehen
(vgl. 
).
Schauen wir uns also zum zweiten Mal zweidimensionale Darstellungen an, und zwar
,
: 
Zu 1. :
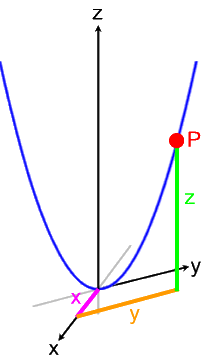
Nun haben wir aber den Teufel mit Beelzebub ausgetrieben: zwar erscheint die Parabel nun als hundsgewöhnliche Normalparabel, mit der wir längst umgehen können müssten, dafür sind aber die Koordinatenachsen sowie die Koordinaten x, y und z arg verzerrt.
Verständlich wird das erst, wenn wir die Normalparabel in ihrem ganz eigenen zweidimensionalen Koordinatensystem betrachten:
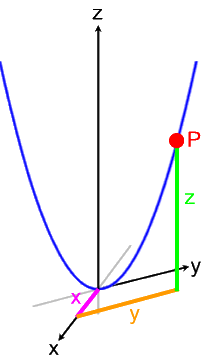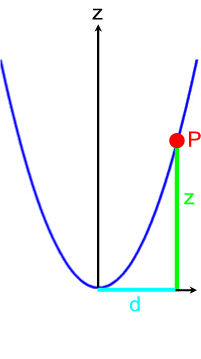
(Spätestens hier wird deutlich, dass die Aufgabe ganz erhebliche Abstraktion verlangt - und man in der Schule unbedingt mit einem dreidimensionalen Modell arbeiten sollte.)
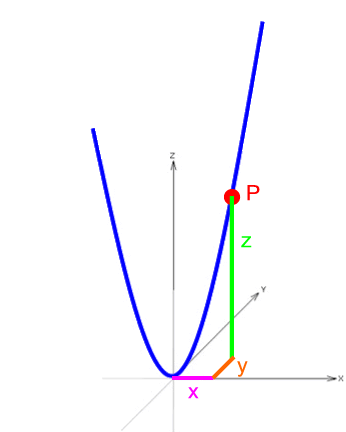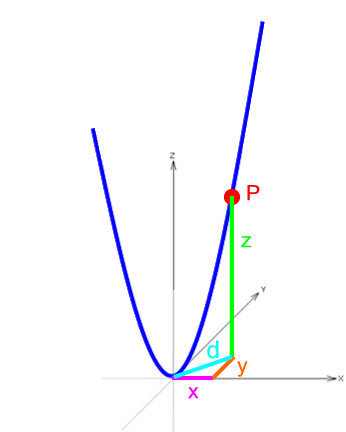
Weil eine Normalparabel vorliegt, erkennen wir aber anhand der Zeichnung
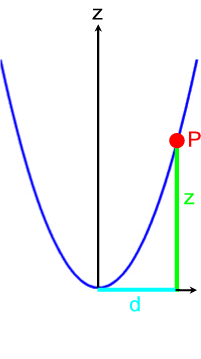
nun, dass
z = d2 *
Dabei ist es geradezu typisch, dass für die Lösung der Aufgabe ein Detail (hier die Strecke d ) benötigt wird, das in der "Aufgabenstellung" gar nicht vorkommt.
(Vgl. 
)
Bemerkenswert ist es aber vor allem, dass d auch in der Sicht von oben auftritt:
Zu 2. :
Hier muss man sich erstmal daran gewöhnen, dass die Parabel, wenn man sie von oben sieht, als Gerade erscheint:
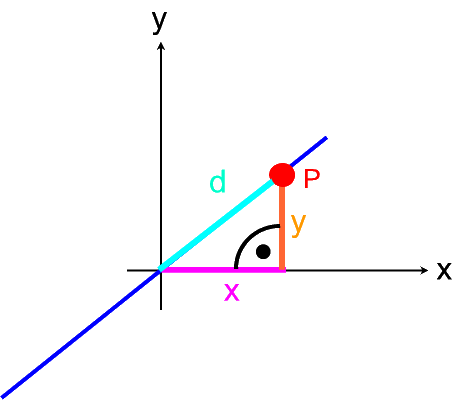
Und auch hier muss man nun etwas ergänzen, was in der Aufgabenstellung nicht mitgenannt ist, nämlich den rechten Winkel und damit die Idee, dass der Satz des Pythagoras anwendbar ist:
d2 = x2 + y2 **
Wenn wir nun aber ** in * einsetzen, so erhalten wir
| z = x2 + y2 , |
womit urplötzlich unser Ziel erreicht ist, z in Abhängigkeit von den vorher gewählten x und y auszudrücken - und womit wir stolz unsere erste dreidimensionale Funktionsgleichung erhalten haben!
Wie schon gesagt, erfordert diese Aufgabe (genauso wie die folgende) einiges Abstraktionsvermögen - und scheint mir deshalb (wieder wie die folgende Aufgabe) besonders geeignet für "gute" SchülerInnen, die ein bisschen Futter statt des ewigen, langweiligen Nachvollzugs brauchen.
Zuguterletzt sei auch noch gezeigt, wo d in der ursprünglichen Projektionszeichnung liegt:
Die Anlässe:
, in dem die Hauptfigur vermutet, dass Spiralen vom ganz Kleinen (der DNA 
) bis zum ganz Großen (Spiralgalaxien) Grundmuster des Universums sind.In der Tat: Spiralen allüberall, nämlich z.B.
(vgl. 
)
(Ist es eigentlich nur Zufall, dass der
Plasmastrom in einem sogenannten
Tokamak-Fusionsreaktor ganz ähnlich aussieht?:
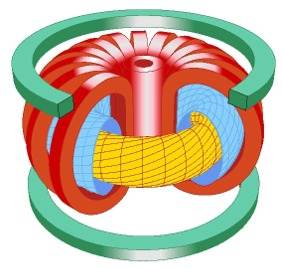
Könnte hinter beiden dasselbe "erkenntnisleitende" "Urbild" stecken?:
)
Und das nicht bloß aus technischer Notwendigkeit, sondern oftmals schlichtweg auch aus ästhetischen Gründen: Spiralen sind "einfach schön", und zwar insbesondere, wenn sie sich gemächlich drehen:
vor aller Mathematik und sowieso aller (vermeintlichen) Anwendung geht es mir hier doch um Schönheit, die beispielsweise auch dadurch belegt wird, dass Spiralen häufig in Architektur und 
Kunst vorkommen.
(Die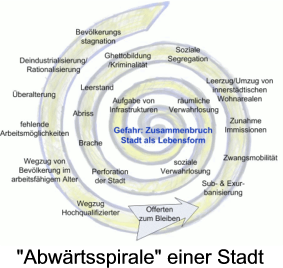 
scheint mit ihrer Abwärtsbewegung und zunehmenden Verengung hingegen wohl eher Zwangsläufigkeit zu bedeuten.)
Wo andere vielleicht nur eine popelige Tomatenspirale, also den reinen Zweck sehen, sehe ich inzwischen fast automatisch eine höchst ästhetische mathematische Grundform; wie es ja bei mir seit geraumer Zeit geradezu eine Manie ist, in alltäglichen Gegenständen mathematische Muster zu erkennen.
(Vgl. 
.)
Vor allem freut es mich natürlich immer, spottbillige alltägliche (!) Gegenstände statt teurer "lebensferner" Mathe-Modelle zu finden.
Meine erste Tätigkeit bei der Tomatenspirale war aber, sie gemäß dem Motto 
in Rotation zu versetzen:
Überhaupt ist für mich jede Spirale in Bewegung:
Vor aller Mathematik scheint mir an der Tomatenspirale die optische Täuschung bemerkenswert, dass sie sich scheinbar nach oben bewegt:
Dieser Effekt scheint mir nur dadurch erklärbar, dass wir die Spirale gar nicht drei-, sondern zweidimensional wahrnehmen, also nicht als rotierend, sondern als feste Sinuskurve, die sich nur nach oben bewegt
(wobei hier nicht geklärt sei, warum die Spirale, von der Seite gesehen, eine Sinuskurve bildet):
Im roten Bereich ist es sogar unklar, ob sich da eine dreidimensionale Spirale dreht oder eine zweidimensionale Sinuskurve nach oben bewegt.
Die gezeigte optische Täuschung wird heutzutage insbesondere bei "Kugelspiralen" benutzt, wie sie in Gartencentern zu bekommen sind:
Die Spirale bewegt sich hier nur scheinbar nach oben bzw. unten, und ebenso bewegt sich die Kugel nur scheinbar in Gegenrichtung, während sie in Wirklichkeit fest in der Spirale liegt.
Gerade die soeben gezeigte zweidimensionale Wahrnehmung werden wir unten aber noch brauchen können.
*
Damit aber zur Mathematik der (Tomaten-)spirale, oder genauer: zu einer ersten Ahnung, wie eine Funktions(?)gleichung herstellbar sein könnte. Ziel ist hier also nicht (wie oben beim Paraboloiden) die vollständige Gleichung, sondern "nur" eine Idee, wie sie zu erreichen sein könnte: 
und kann doch ein Grundverständnis gewinnen.
Im Folgenden betrachten wir nun vorerst nicht mehr die rotierende, sondern die feststehende Spirale, auf der sich ein Punkt P hoch bewegt
(Die feststehende Spirale wird also eben doch wieder durch Bewegung erklärt):
Es geht also vorerst um die Funktions(?)gleichung der festen Spirale, die wir dann erst später in Rotation versetzen.
Um nun die "Funktionsweise" der (festen) Spirale besser zu verstehen, schauen wir sie uns erstmal von oben an:
Die Spirale sieht von oben wie ein Kreis aus, der hier allerdings perspektivisch wie eine immer enger werdende ( logarithmische) Spirale wirkt.
Eine schöne Veranschaulichung für die Kreisform ist auch ein Besenstiel, den man passend längs durch die Tomatenspirale schieben kann:
Von oben gesehen bewegt sich der Punkt P also auf einem Kreis,
(wobei nicht erkennbar ist, dass er sich auch aufs Auge zu bzw. von ihm weg bewegt):
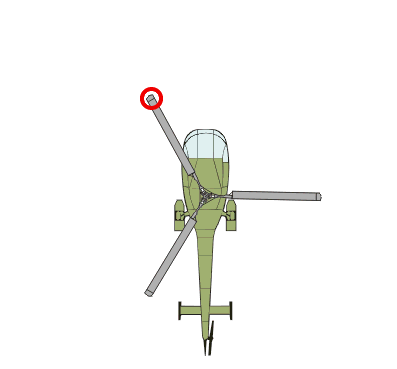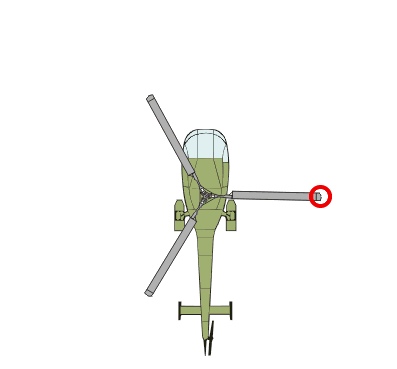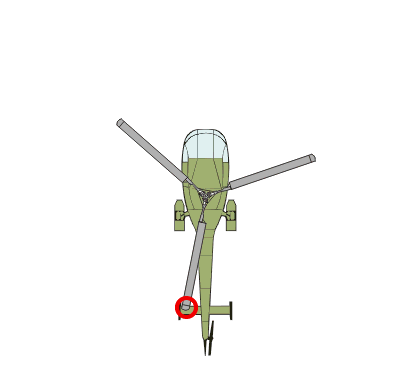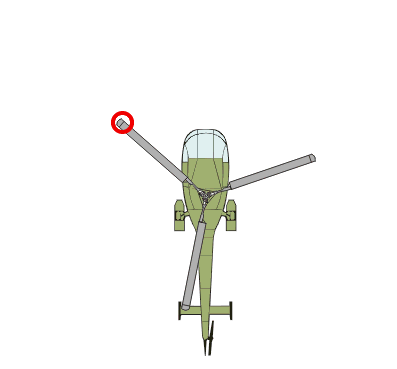
Das ist vergleichbar mit einem Hubschrauber, der noch auf der Erde steht, dessen Hauptrotor sich aber schon dreht:
Diese Kreisbewegung ist aber sehr einfach durch die Kreisgleichung x2 + y2 = r2 erfassbar, wobei r der Radius ist
(hier müsste zusätzlich noch der Zeitfaktor t eingefügt werden, der angibt, in wieviel Sekunden der Punkt P sich einmal vollständig im Kreis bewegt).
Zusätzlich bewegt sich der Hubschrauber aber noch gleichmäßig nach oben, was durch die einfache lineare Gleichung z = t ∙ m darstellen, wobei t die Zeit ist und m ein Faktor, der die Geschwindigkeit des Abhebens nach oben bestimmt
(also z.B. m = 30 cm pro Sekunde):
(Nebenbei: man kann die Hubschrauberbewegung sehr schön mit einem sogenannte
Flugkreisel
vorführen, und zwar idealerweise so, dass man ihn im Dunkeln startet und an einem Rotor - wie? - eine klitzekleine Lampe installiert.)
Die endgültige Gleichung ergäbe sich dann durch Kombination der Kreis- und der linearen Gleichung.
Oben hatte ich schon mit Bedacht "Funktions(?)gleichung" geschrieben, weil nach unserem Verfahren ja gar keine Funktion herauskommt, da mehrere
(bei unendlich langer Spirale periodisch unendlich viele)
Punkte der Spirale übereinander liegen.
*
Es gibt allerdings noch eine andere schöne Perspektive auf die Spirale, die wir erhalten, wenn wir sie
Sowohl von vorne als auch von oben sieht die Spirale sinusförmig aus
(und den zweidimensionalen Sinus beherrschen wir ja schon).
Und wenn wir beide zweidimensionalen Perspektiven kombinieren, ergibt sich eben die dreidimensionale Spirale:
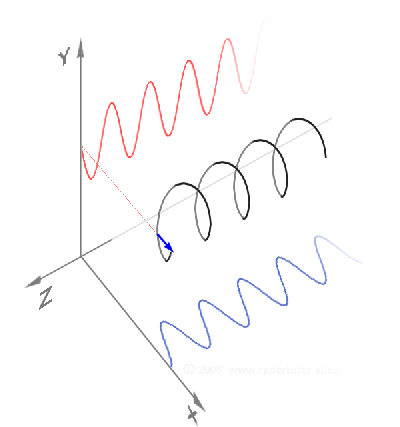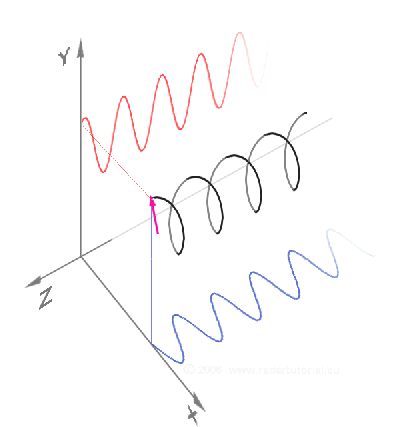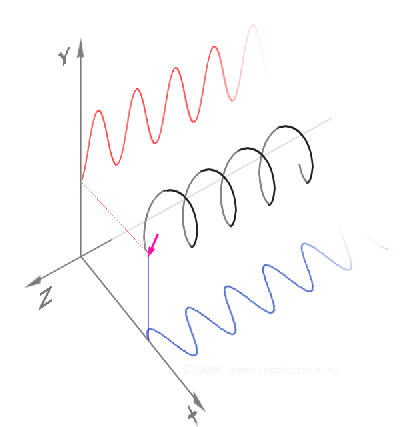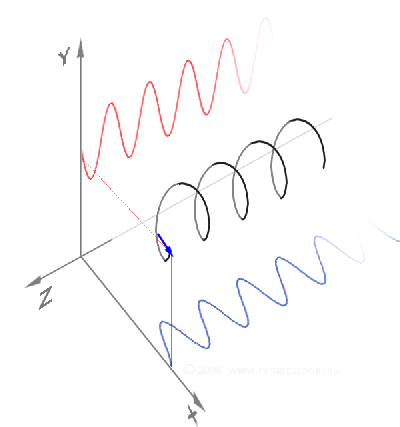
(Quelle: , wobei hier die Koordinatenachsen anders angeordnet sind als oben)
(Quelle:
)
Und umgekehrt könnte man aus der Spirale mittels Polarisation (s.o.) wieder die beiden Seitenansichten gewinnen:
Nebenbei: hier käme tatsächlich eine Funktions(!)gleichung heraus.
*
Mit beiden Modellen haben wir aber "nur" Gleichungen für die ruhende Spirale angedeutet. Diese müsste nun noch mit einem "Zeit-Zusatz" in Drehung versetzt werden.
*
Der durch die Tomatenspirale gezogene Besenstiel
zeigt auch, wie man ohne viel Aufwand und großartige Überlegungen eine Spirale erhalten kann: man wickelt einfach ein Band schräg um einen Besenstiel:
*
Und aus zwei Tomatenstangen kann man schön eine Doppelspirale bzw. eine Doppelhelix à la DNA flechten:
*
Durch eine "Tomaten"-Spirale kann man natürlich auch eine Bohnenpflanze wachsen lassen
,
und bei solch einer Bohne ergibt sich ein netter zusätzlicher Effekt bzw. eine weitere mathematische Herausforderung:
Um die gewundene "Tomatenspirale" windet sich wiederum die Bohnenpflanze.
Es ist, als wenn auf dem Rotor eines großen Hubschraubers nochmals ein kleiner Hubschrauber montiert ist und wir nun die Bewegung des Punktes Q betrachten:
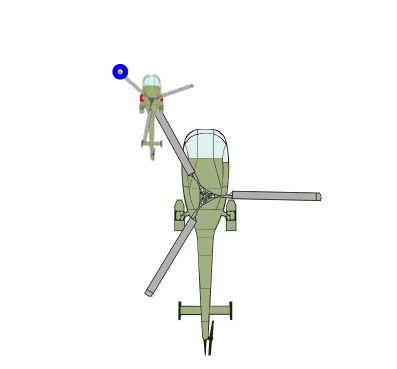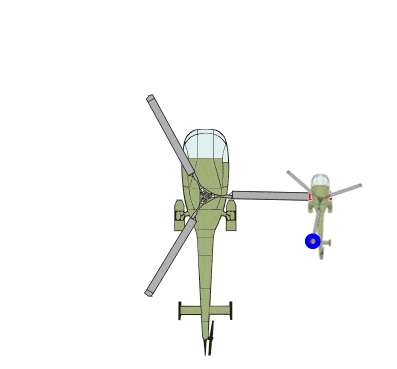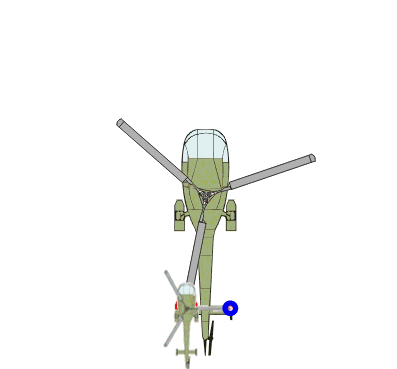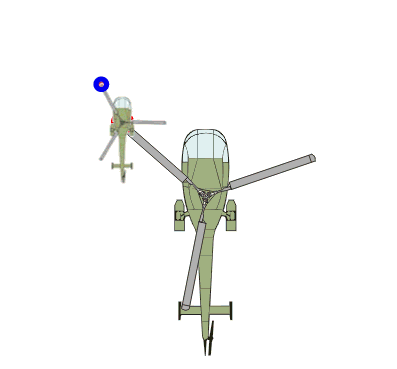
Der Punkt Q bewegt sich dabei
,
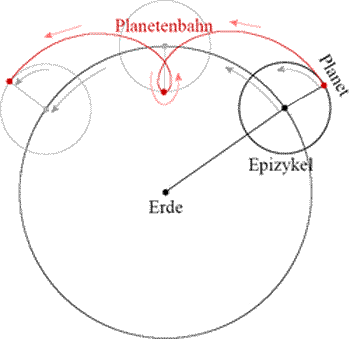
(wie laut alter ptolemäischer Theorie die Planeten oder wie die Sitze auf dem Karussell 
),
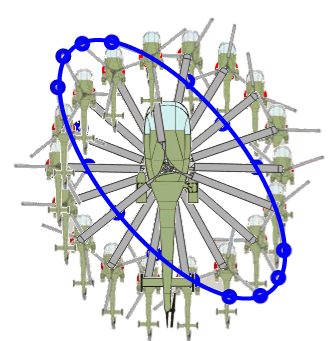
auf sogenannten Epizykeln
(kleinen auf großen Kreisen):
(Überhaupt wären ja die Bewegungen moderner Kirmes-"Karusselle" ein interessantes mathematisches Forschungsgebiet.
Vergleiche ansonsten auch 
)
*
Auch schöne Aufgaben:
Kreisel- und Spiralbewegungen
(wobei es für mich letztlich unverständlich-wundersam bleibt, weshalb ein Kreisel sich selbst stabilisiert):
|
PS:
